磁路分析与计算技巧

1.磁路基本概念

（1）磁路概念 磁路作为一种简化的电磁系统计算方法，目前在工程计算中应用还比较广泛。将磁通看成在磁通管内流动着的物质，就像电流在电导体中流动一样，因此磁通相当于电流，磁通管相当于载流导体，磁场就相当于类似电路的磁路，这样就将磁场路化。对于绝大多数工程电磁系统的磁场，以磁导率非常大的铁磁材料作为磁通的主要路径，磁场中的磁通基本上是沿着磁导体形成的接近于闭合的回路流动，因此可以将磁导体的外壁看成磁通管，根据磁导体的几何参数计算磁路各段的磁阻，这样就利用磁路的概念将磁场问题变换成磁路问题，磁场的计算就可以根据磁路的基本定律进行计算，从而使电磁系统的计算大为简化。

（2）磁路计算的基本定律 由磁通连续性定理导出磁路基尔霍夫第一定律：

∑∅=0 （4-195）

式（4-195）表明：对于磁路中的任一节点，进入该点的磁通之和等于自该点流出的磁通之和。

由安培环路定律导出磁路基尔霍夫第二定律：

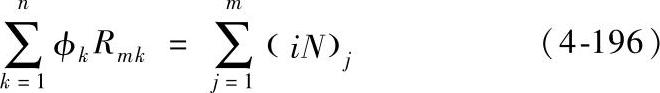
式（4-196）表明：对于磁路中的任一闭合回路，磁动势的代数和等于该回路各段上磁压降的代数和。

磁路欧姆定律：

U_m=∅R_m （4-197）

式（4-197）表明：磁路两端的磁压降等于通过磁路的磁通与其磁阻的乘积。

（3）磁路与电路的异同 磁路与电路有许多相同之处，表现在磁路中的磁动势、磁通、磁压降、磁阻、磁阻抗等参量与电路中的电动势、电流、电压降、电阻和阻抗等参量一一对应。磁路欧姆定律和基尔霍夫定律与电路的同名定律之间也存在对应关系。然而，磁路和电路之间有本质上的差异。电路是带电粒子实际运动的路径，其中确有带电粒子作定向运动；磁路和磁通是借以分析磁场问题的一种手段，并没有实体的磁通。

（4）磁路的特点

1）由于磁导体的相对磁导率通常并非常数，而是磁感应强度B的函数，因此一般磁路是非线性的；

2）磁导体与一般媒质的磁导率比值通常只有10³～10⁴，工程计算中忽略漏磁通会给计算带来较大误差；

3）磁通和漏磁通不会产生焦耳热损耗；

4）磁导体外部的磁通管的几何参数一般均属未知，与它相关的磁路参数应根据磁场的基本性质的基本定律确定；

5）由于必须考虑漏磁通，磁路中的磁动势和磁阻都是分布参数，因此磁路是分布参数性质的路。

2.气隙磁导的计算

电器中各种形式的电磁系统一般都具有空气隙，气隙磁导的大小取决于构成气隙的极面的几何形状和相对位置，以及气隙的磁场分布情况。由于气隙磁场分布比较复杂，准确计算气隙磁导是非常困难的。为了简化计算，工程上常假定：

1）空气的磁导率等于真空的磁导率；

2）把导磁体表面看作等磁位面，磁力线都垂直于导磁体表面。

气隙磁导计算的准确度，对磁路计算的结果影响很大。在设计计算中常用解析法和分割磁场法计算气隙磁导。尽管磁导体部分的磁路长度比气隙大得多，但由于空气的磁导率仅为磁导体的10^-3～10^-4，因此气隙磁阻远比磁导体的大，要准确计算磁路，首先必须准确计算气隙磁导。下面讨论气隙磁导的计算。

应用解析方法，对于磁极间的磁力线均匀分布的理想情况，可以通过式（4-198）计算气隙磁导：

式中 Λ_δ——气隙磁导；

δ——气隙长度；

A——气隙截面积；

μ₀——空气隙的导磁系数。

实际上由于气隙间的磁力线相互排挤，磁通向外扩散，磁极的边缘部分磁力线分布不均匀，按式（4-198）计算气隙磁导就会带来较大误差。但式（4-198）是计算气隙磁导的基础，若磁极形状为规则的几何形状、气隙内的磁通和等位线分布均匀，而且忽略磁极的边缘效应及磁通的扩散，可以运用磁场理论和数学推导直接求得气隙磁导的计算公式，见表4-28。

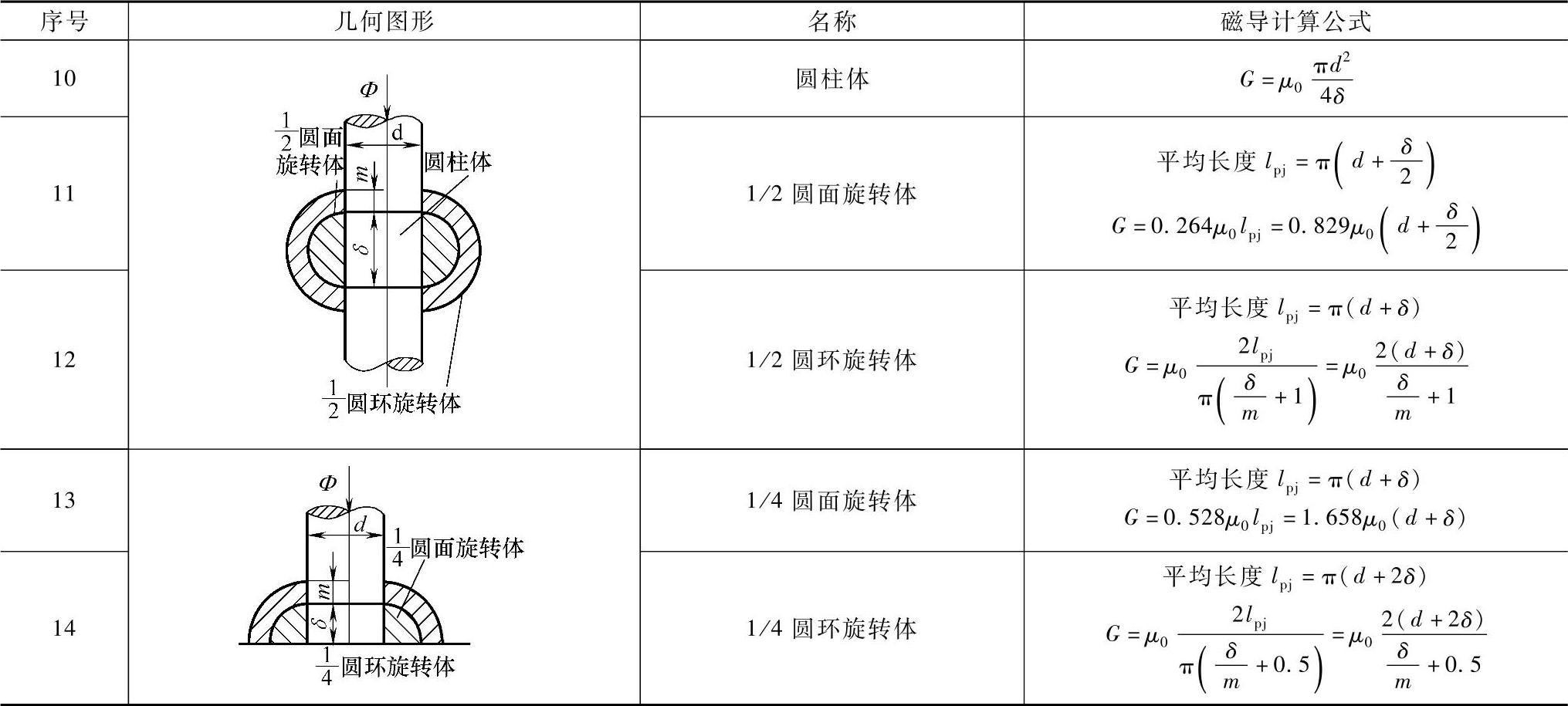
当磁极几何形状比较复杂通常采用磁场分割法来计算气隙磁导，磁场分割法是首先确定磁极之间气隙磁场的分布规律，估计磁通的可能路径，将整个气隙磁场划分为若干个有规则形状的磁通管，分别按式（4-198）求出磁导，最后根据磁通管的串并联关系得出整个气隙的磁导。磁场分割法满足工程计算所需准确度，并且计算方便，在电磁系统设计计算中广泛应用。表4-29中列出各种常见磁通管磁导的计算公式，便于计算时查取。

表4-28 用解析法推导的规则几何形状磁极的气隙磁导计算公式

（续）

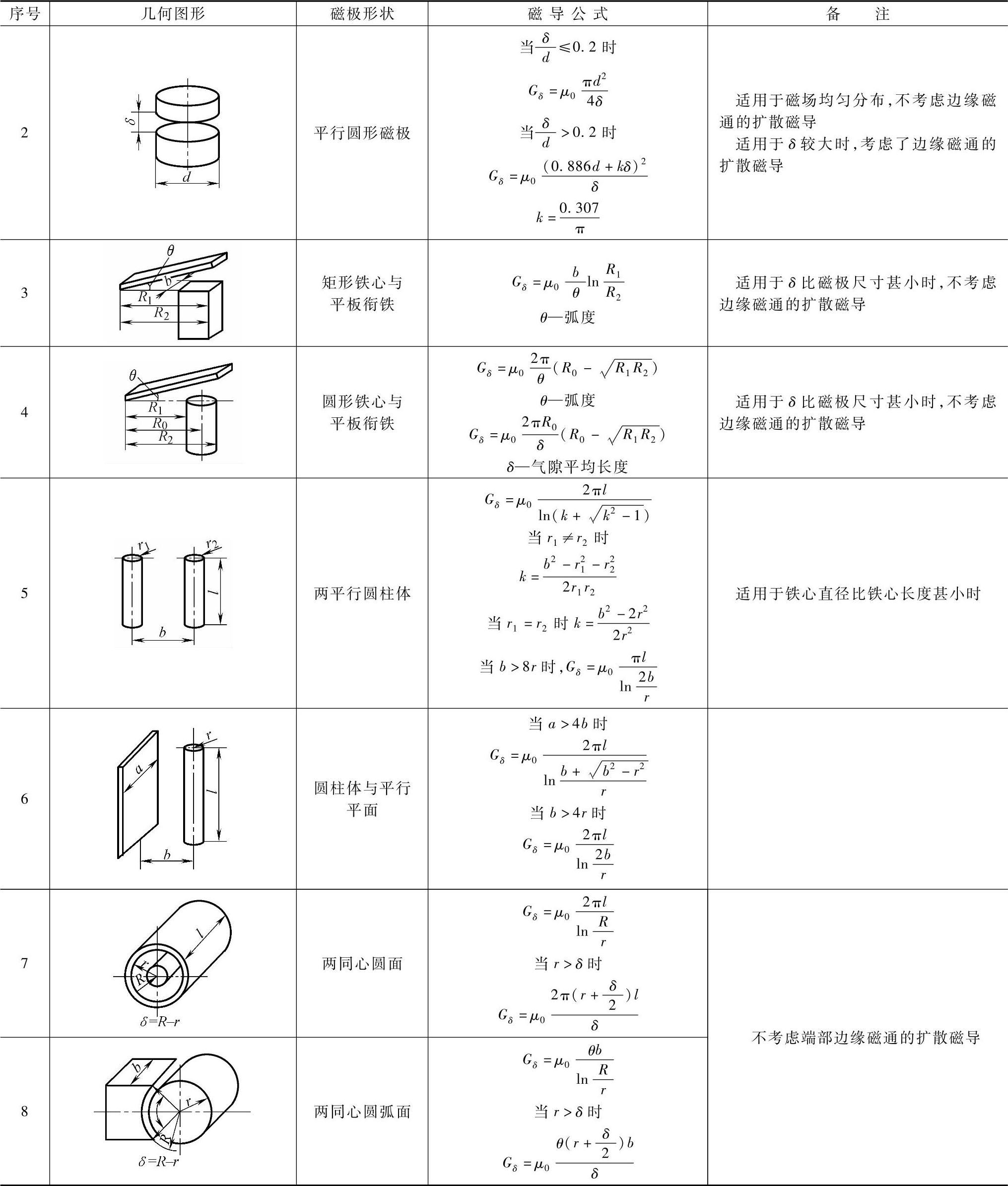
表4-29 若干磁通管的气隙磁导计算公式

（续）

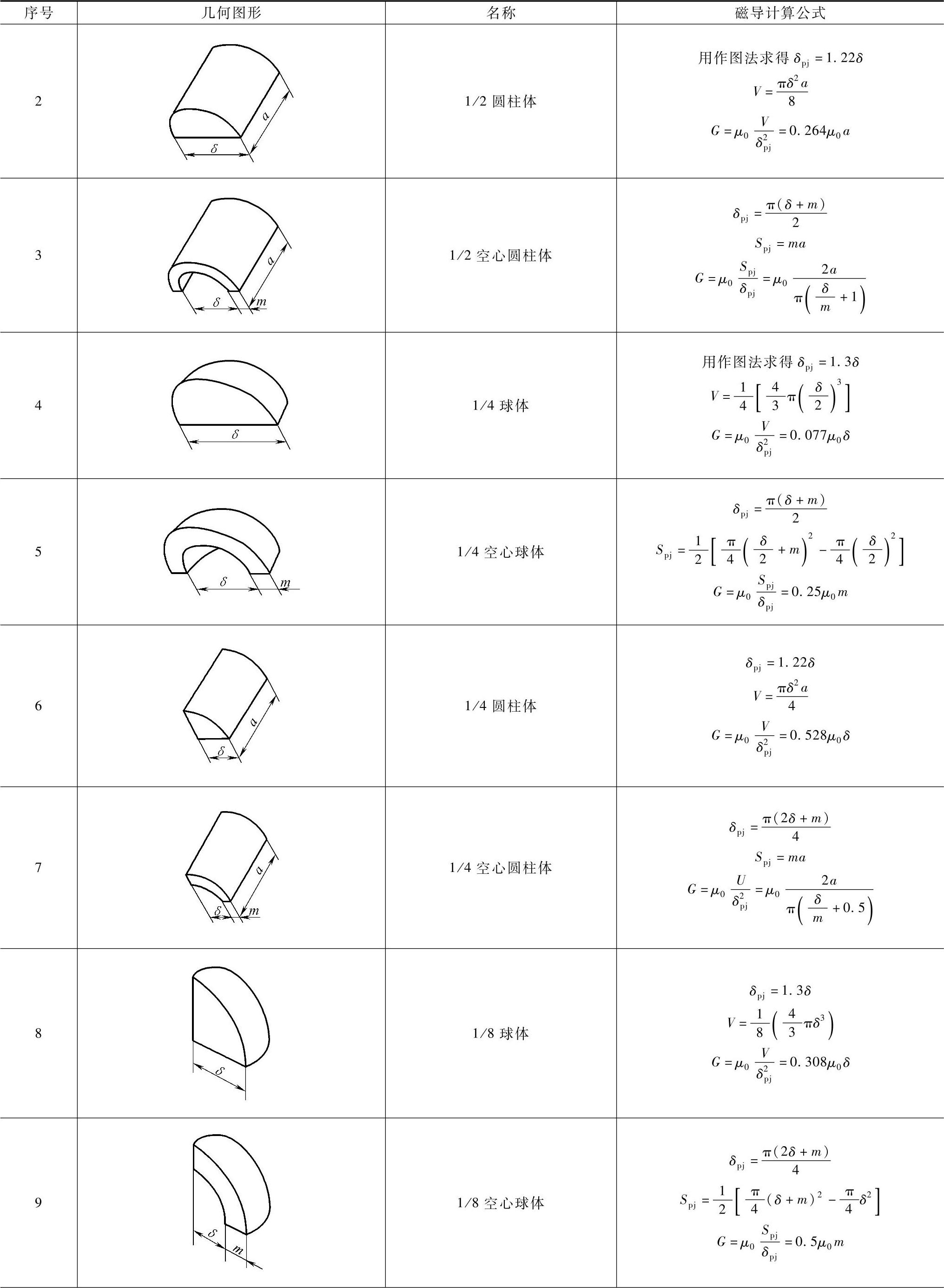
（续）

3.直流磁路分析与计算(www.xing528.com)

磁路计算的复杂性就在于漏磁分布性和铁心磁阻的非线性，同时漏磁的分布性使得铁心磁阻也带有分布性，铁心磁阻的非线性又使得漏磁计算也在非线性问题中考虑。另外，作为场源的套于铁心柱上的励磁线圈产生的磁动势也是沿铁心长度分布的。因此，磁路是兼具分布性和非线性的路径，求解比较困难，一般采用近似方法求解。

（1）漏磁通的处理 漏磁通的路径和分布规律在磁路计算中比较重要，因为等效磁路主要根据它作出。但漏磁通的分布异常复杂，而且随电磁系统结构不同而异，没有通用的方法准确确定漏磁通的路径和分布，近似的方法如下：

1）实验法：当电磁系统具有实物或模型时，可通过实验大致确定漏磁通的路径和分布情况。

2）作磁位分布图形法：根据参考点画出磁动势、磁路上的磁压降和磁位分布图，则存在磁位差的空间必定有漏磁通，即可确定漏磁通的分布。

3）运用磁场图景的方法：根据磁场性质描绘磁场图景，确定漏磁通的路径和分布规律。

（2）直流磁路的计算 对于大多数实际电磁系统的漏磁，将其看成集中的参量方便计算，此时等效磁路是多回路的非线性磁路，可以借鉴求解复杂直流电路的节点电位法、回路电流法，采用节点磁位法和回路磁通法进行计算。

直流磁路的特点是在稳定工作时，线圈中的励磁电流I与工作气隙δ的大小无关，即线圈磁动势IN等于常数。

在电磁系统的结构尺寸给定的情况下，直流磁路计算的任务有两类：

1）已知工作气隙磁通Φ_δ，求线圈磁动势IN；

2）已知线圈磁动势IN，求工作气隙磁通Φ_δ。

由于磁路的分布性和非线性，工程上一般采用分段法和漏磁系数法计算直流磁路。

分段法是将分布参数磁路简化为若干个集中参数磁路的计算方法，由于磁路的分布性，磁导体材料的磁导率在整个磁路中处处不同，因此将电磁系统分成若干段，在每一段内将磁动势和漏磁通都看成集中参量进行计算。分段法的实质是认为磁导体中各段内的磁通不变，这样方便非线性磁阻的计算。分段数越多，计算结果越准确，但计算工作量也越大，因此在计算时根据实际情况选择合适的分段数即可。分段法适合当磁路各部分截面积不等，或单位长度漏磁导非常数的情况。

漏磁系数法是工程上常用的比较简便的近似计算方法，漏磁系数是指铁心中任一截面内的磁通与气隙磁通之比。在铁心柱的任一截面内，其磁通可表示为气隙磁通和该处至气隙的全部漏磁通之和，即

Φ_y=Φ_δ+Φσ=σ_yΦ_δ （4-199）

式中 σ_y——漏磁系数。

下面通过一个实例介绍漏磁系数法的应用。如图4-170所示的拍合式电磁系统，由于线圈磁动势是分布的，考虑漏磁通，则沿铁心和铁轭的高度，导磁体各处的磁通是不同的，为便于计算，将铁心底部的总磁通Φ₀对工作气隙磁通Φ_δ的比值定义为漏磁系数。忽略铁磁体和非工作气隙磁阻时的等效磁路如图4-171所示。

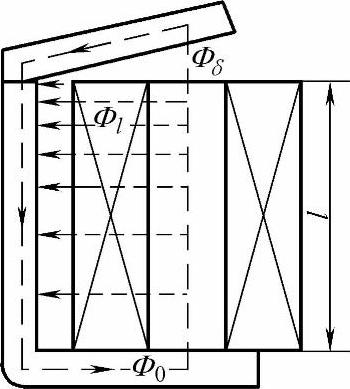
图4-170 拍合式电磁系统磁通分布

图4-171中用一个集中磁动势IN代替实际上为分布的线圈磁动势，用一个靠近工作气隙处的集中漏磁导G_∅按漏磁通不变的原则等效分布的漏磁导，因此

式中 g——铁心单位长度的漏磁导；

l_c——产生漏磁的铁心长度。

漏磁系数：

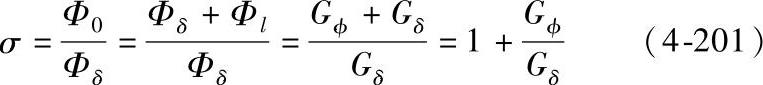
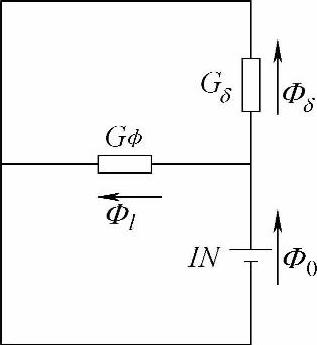
图4-171 忽略铁磁体和非工作气隙磁阻的等效磁路

首先根据气隙大小计算工作气隙、非工作气隙磁导和铁心单位长度漏磁导，根据上式计算漏磁系数。

对已知工作气隙磁通Φ_δ，求线圈磁动势IN的正求问题，根据气隙的磁通和漏磁系数可以计算铁磁体的磁通，根据磁路欧姆定律，由磁通和磁路长度计算铁磁体上的磁压降，以及工作气隙和非工作气隙的磁压降，最后利用安培环路定律计算线圈磁动势IN。

对已知线圈磁动势IN，求工作气隙磁通Φ_δ的反求问题，先假设一气隙磁通求线圈磁动势，根据结果调整假设值，辅之以作图，即可求解。

4.交流磁路分析与计算

交流磁路与直流磁路相比有以下特点：

1）交流磁路中的电压、电流和磁通都是交变的。为了简化计算，认为它们的波形都是正弦的。磁路计算时，磁通和磁通密度用幅值表示；电压、电流、磁动势和磁场强度均用有效值表示。

2）由于交变磁通的作用，在导磁体中产生磁滞和涡流损耗使磁通与励磁电流不同相。磁路计算时，磁路的欧姆定律和基尔霍夫两定律仍然适用，但应采用复数形式。

3）对于交流并励电磁系统，由于外加电压是固定的，因此磁链基本上是固定的，不随工作气隙的大小变化，而线圈电流则与气隙大小有关。

交流磁路的计算方法大体上与直流磁路相同，但有其特点。对于交流串励交流电磁系统，线圈电流不随气隙改变，其磁路计算方法与直流磁路完全相同。而交流并励电磁系统为恒磁链系统，其磁路计算方法不同于直流磁路计算方法。

交流磁路的分析方法有等效正弦波形法和波形分析法，等效正弦波法适用于铁心未充分饱和或气隙较大，波形畸变不严重的情况，通过有效值相等的正弦波电压（电流）表示畸变的电压（电流）。分析时磁路的各种参数均以相量和复数表示。波形分析法适用于无气隙且经常工作于饱和状态的磁路，特别是磁导体具有接近于矩形或直角形动态磁滞回线的磁路。

交流并励电磁系统的计算任务有两类：

1）已知工作气隙磁通Φ_δ，求线圈磁动势IN；

2）已知电源电压U，线圈匝数N，求工作气隙磁通Φ_δ和线圈磁动势IN。

对于任务1：首先是作等效磁路图，计算全部的磁阻和磁抗，由计算的磁阻、磁抗和已知的磁通，根据交流磁路欧姆定律计算漏磁导两端的磁压降，根据基尔霍夫定律计算各部分磁通，最后由交流磁路的安培环路定律计算线圈磁动势。

对于任务2：先根据给定的U值，按U=4.44fNΦ_m 先假设一个气隙磁通值，然后按正求任务计算U，将所得U值与给定的U值加以比较，不断调整假设值，直到两者相等或满足准确度要求即可。