计算导体电动力的典型方法

作用在导体上的力是电流与磁场相互作用的结果。事实上电流的单位安培就是由两根平行导线通过同向电流而引起的吸力来定义的，1A就是当通过这个电流时相距1m远的两根导线产生的单位长度吸引力为2×10^-7N/m。

导体上受到的电动力可由毕奥-沙伐定律来计算，电动力等于

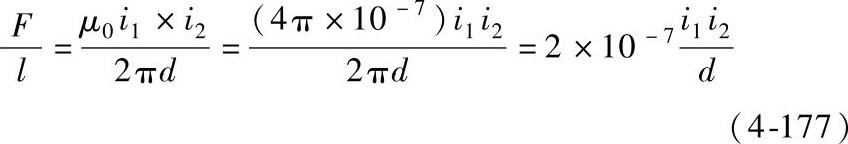
式中 F——电动力（N）；

l——导体长度（m）；

d——导体之间距离（m）；

i₁、i₂——电流（A）；

μ₀——磁导率常数（Wb/Am），μ₀=4π×10^-7 Wb/Am。

从上述方程可知，两个导体间的电动力与导体中的电流i₁和i₂成正比，与磁导率常数成正比，还与导体间的几何位置所决定的常数成正比。正如前面所提到的，复杂几何形状的电动力计算需要在计算机的帮助下才能完成。

一个导体上受到的总电动力可以用导体上每一部分受到的力进行叠加得到，当然这每一部分的力并不单独存在，用每一段的力进行叠加只是为计算带来方便，在计算时要注意构成电流回路的每一段导体都要考虑到，不要遗漏。

母线排的电动力计算是开关设备中最典型并且相对简单的情况，下面我们就此进行分析。

1.平行导体

当导体截面为圆形，且导体长度为无限长的情况下，毕奥-沙伐定律可直接用于计算平行导体间的电动力。公式适用的条件是导体的长度与导体间距离的比大于10，在这种情况下计算误差小于10%，可以满足工程上确定导体强度的需要。

对于导体长度为有限长的情况下，可采用Frick给出的公式：

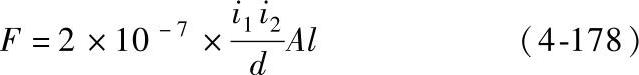
式中

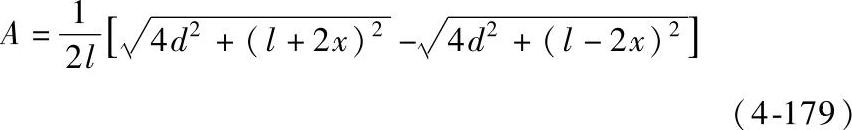
系数A还示于图4-162中，图中右上角的方框中示出导体的l和x以及它们之间距离d的关系。

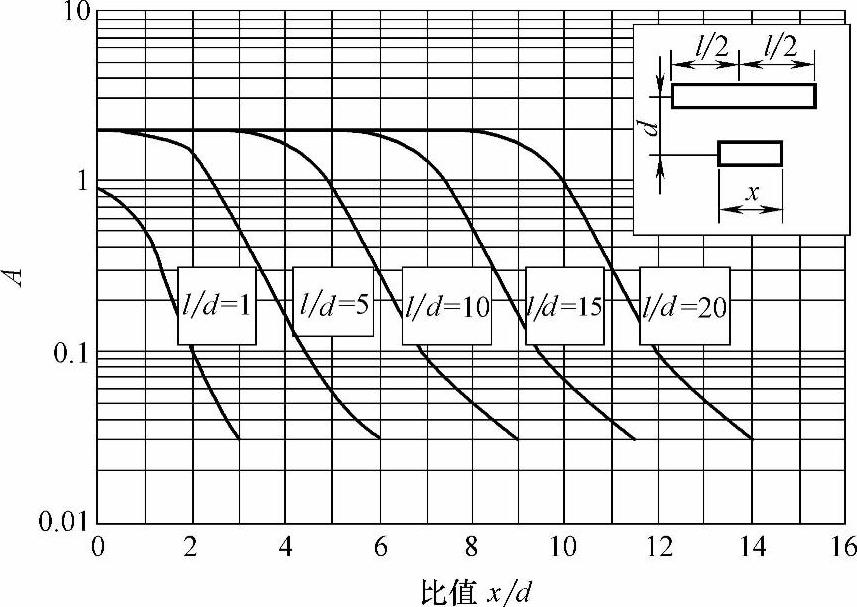
图4-162　一对平行布置的短导体电动力计算中的系数A

截面为矩形的导体电动力计算公式与圆截面导体一样，只是公式中要乘上一个截面因子K。截面因子中要考虑导体的宽度、厚度和导体间距离，并且要考虑电流并不一定集中在导体中心。由Dwight计算得到的截面因子K示于图4-163中，由图中可以看出当（d-h）/（h+b）＞2时，导体形状引起的误差已经很小，可以不考虑截面因子的影响。

2.导体间有夹角

电动力的方向已经在4.12.3节中介绍了，但是在此为了方便起见，还是要把电动力方向的规律重新提一下：当一个垂直折弯的导体，电流从一臂流入，从另一臂流出，导体上的电动力指向折弯的外面，即试图使折弯拉直；当电流从折弯的两臂同时流入或同时流出时，导体上的电动力指向折弯的里面，即试图使折弯并拢在一起。

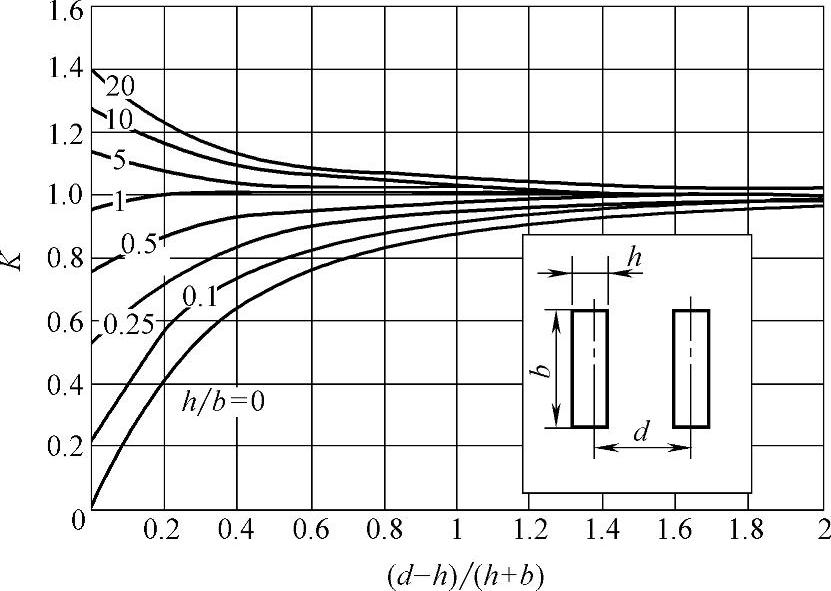
图4-163　矩形截面平行导体的截面因子K

当第一个导体与第二个导体呈垂直布置，第二个导体在距离转弯点为y处所受到的总电动力为

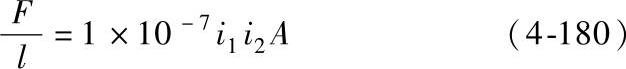
式中 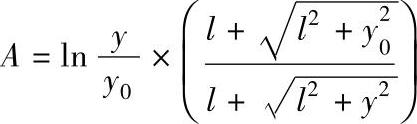（见图4-164）；

l——第一导体的长度；

y——第二导体的长度；

y₀——对于圆截面导体为0.779乘以导体半径，对于矩形截面导体为0.224乘以（a+b），a和b为矩形截面尺寸。

导体长度不同时的系数A也示于图4-164中。

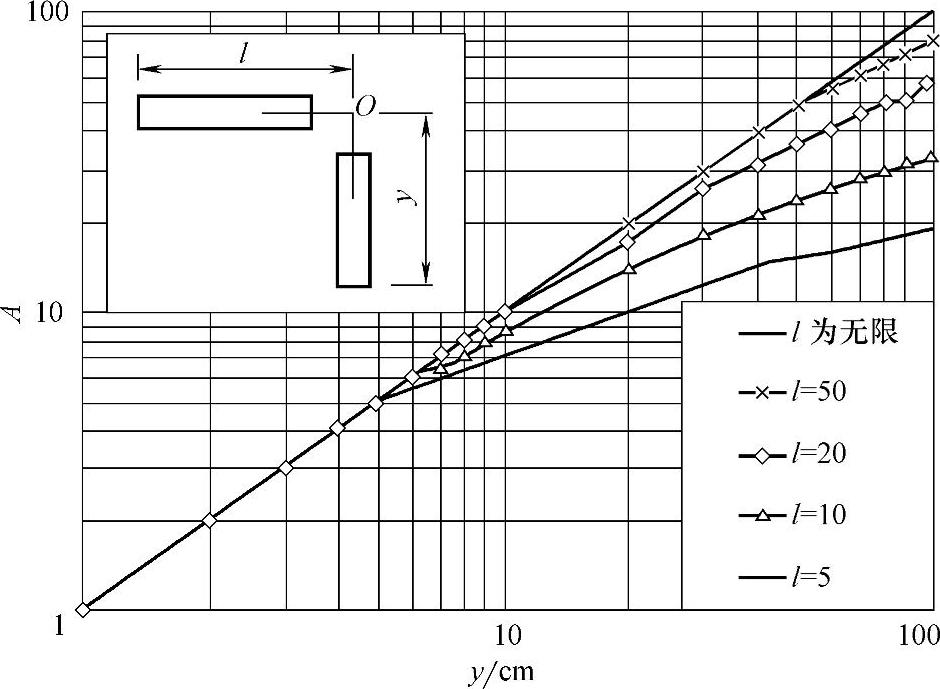
图4-164　垂直布置导体中一个导体上的一点受到的总电动力计算中的系数A

为了计算总电动力相对于O点的转矩，对于O点位于折弯点的情况可用下式计算：

M_o=1×10^-7i₁i₂D （4-181）

式中　D——系数（见图4-165）。(www.xing528.com)

3.触头间的电动斥力

从4.10节我们知道电流在一对触头中流过时会收缩到一个很小的区域中，如图4-166所示。沿触头表面流动的电流会产生一个使触头斥开的力F_B，

式中 μ₀——真空中磁导率常数；

I——瞬时电流值；

R——触头半径；

a——收缩点半径平均值。

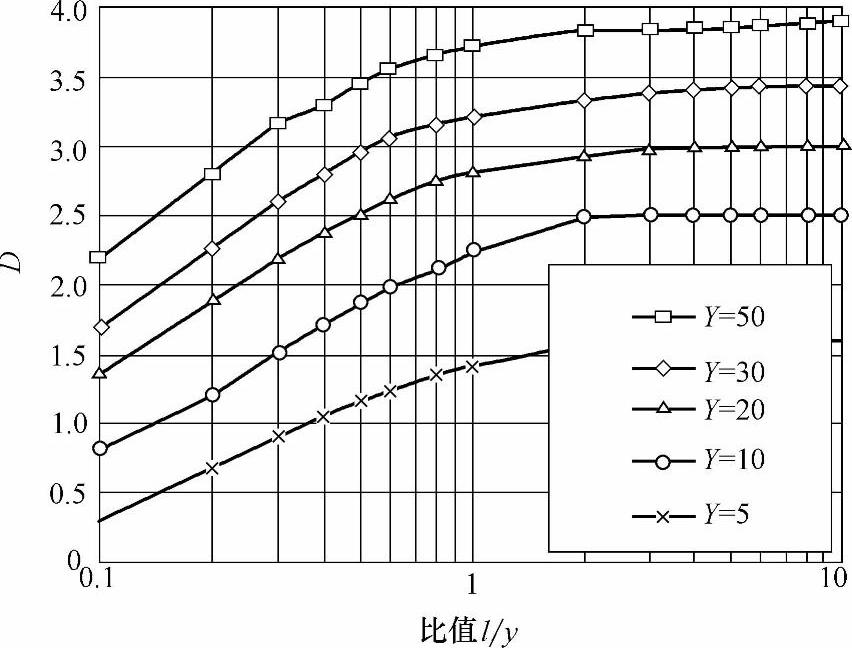
图4-165 计算作用在导体上的力矩（相对于图4-164中O点）时所用的系数D

由于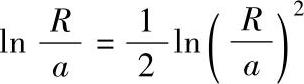，并借助于4.10节式（4-91）可得

式中 A——触头表面总面积。

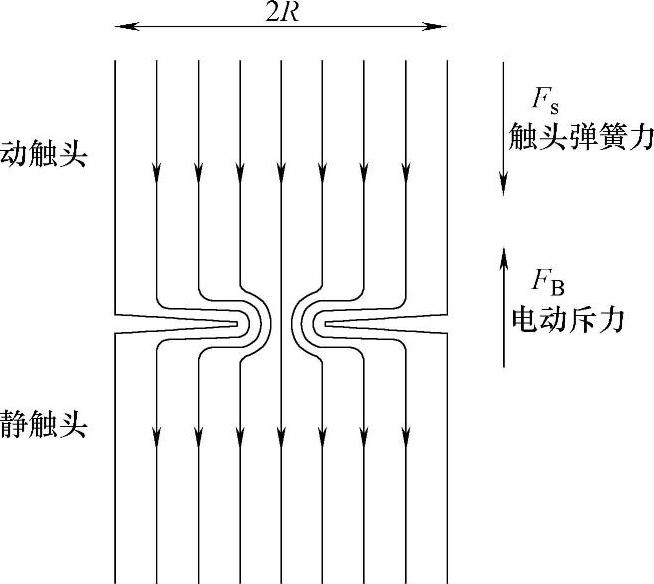
图4-166 一个大电流通过触头斑点时产生斥力

式（4-183）的缺点在于当触头斥力增加时，触头压力F在减小。Barkan对这个问题进行了分析，给出总触头压力F为

F=F_s+F_A-F_B （4-184）

式中 F_s——触头弹簧压紧力；

F_A——触头回路电动力，这个力通常设计成能够部分抵消触头斥力，其表达式为

F_A=KI² （4-185）

式中 K——常数。

将式（4-183）中的F用式（4-184）代替得

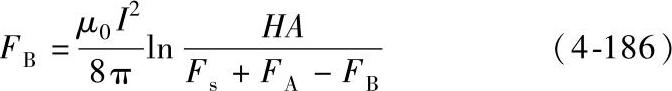
因为F_B出现在方程的两端，所以这是一个隐式方程，不易直接求解。Barken将式（4-186）变成如下形式：

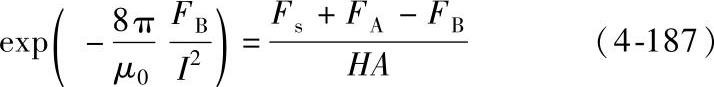
Barken指出如果方程（4-187）的右端项=α₁，左端项=β₁，那么当α₁=β₁并且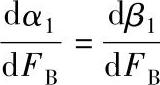时可得到式（4-187）的解。由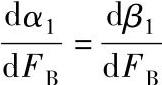可得出

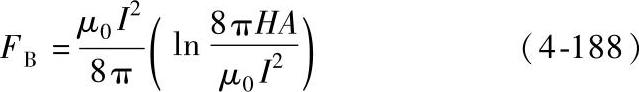
将式（4-188）的F_B代入式（4-187）中，可得需要的最小触头弹簧力为

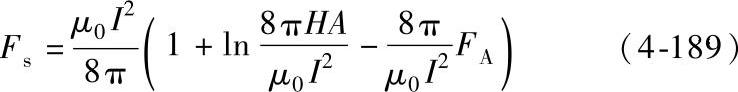
当触头为如图4-166所示的平板对接式情况时，此时F_A=0，这样方程（4-189）可简化成：

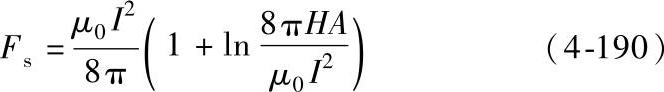
图4-167示出在高真空中的平板对接式触头为克服触头斥力所需的触头弹簧力数据，由图中可以看出式（4-190）与实验结果相符很好。图4-167中式（4-190）所描述的克服触头斥力所需的触头弹簧力曲线可以用下式表示为

F_s=4.45×10^-7I² （4-191）

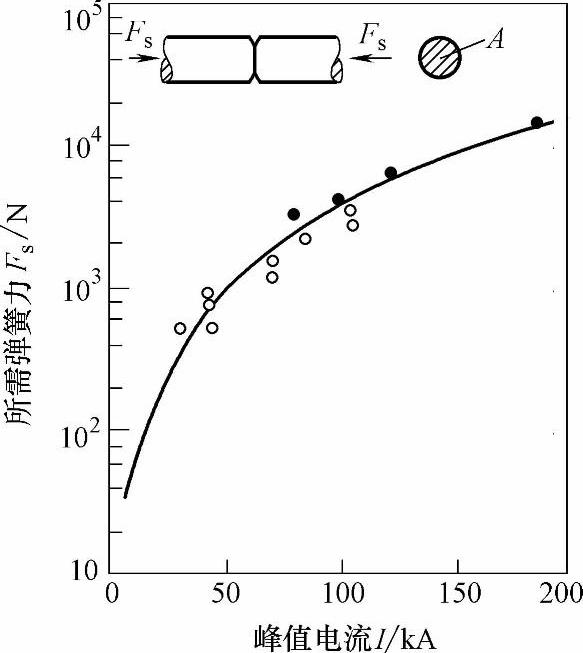
图4-167 用以克服大电流通过平板对接触头的触头斥力所需的触头弹簧力

如果触头一旦被电动力斥开，则斥力随触头间隙的增加而迅速减小。但是如果触头斥力足够大，使得触头分开一定距离并产生电弧，则电弧区被加热的气体所产生的力足以维持触头处于这个开距下，这种触头间距离很近情况下产生的电弧有时叫做悬浮电弧，它能够使得触头材料严重磨损，还可能导致严重的触头熔焊。