短路电流对发热和稳定性的影响

断路器必须能经受短路电流的考验。在一定时间内断路器承受短路电流引起的热作用而不致损伤的能力称为断路器的热稳定性。短路时导体的热计算主要是校核其热稳定性。

导体通过短路电流的时间很短，只有几秒钟。在这么短的时间向外传出的热量很少，所以可以忽略这部分热量。这时，全部热能都储存在导体内，使导体温度升高，这种热量不向发热体以外发散的过程称为绝热过程。绝热过程中导体温度升高的计算方法如下：

设有一导体，长为l，截面积为A，如图4-159所示。从t=0开始，流过短路电流I_s，产生的损耗为P₀，导体在通电前温度为θ₀，通电后温度为θ。由于短路时导体温度迅速增加，因而应考虑电阻率ρ随温度的变化，故损耗功率P不是一个常数。这时导体的能量平衡方程为

Pdt=C_tdθ （4-164）

式中 C_t——导体的热容量（J/K）。

热容量C_t的意义是导体温度每升高1K所需要的热量。C_t可由下式决定：

C_t=cG （4-165）

式中 G——导体的质量（kg）；

c——导体材料的比热容[J/（kg·K）]。c的意义是1kg材料每升高1K所需要的热量。

几种常见材料的比热容c见表4-26。

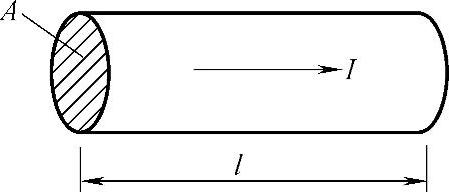
图4-159 导体的发热

表4-26 常用材料的比热容与密度

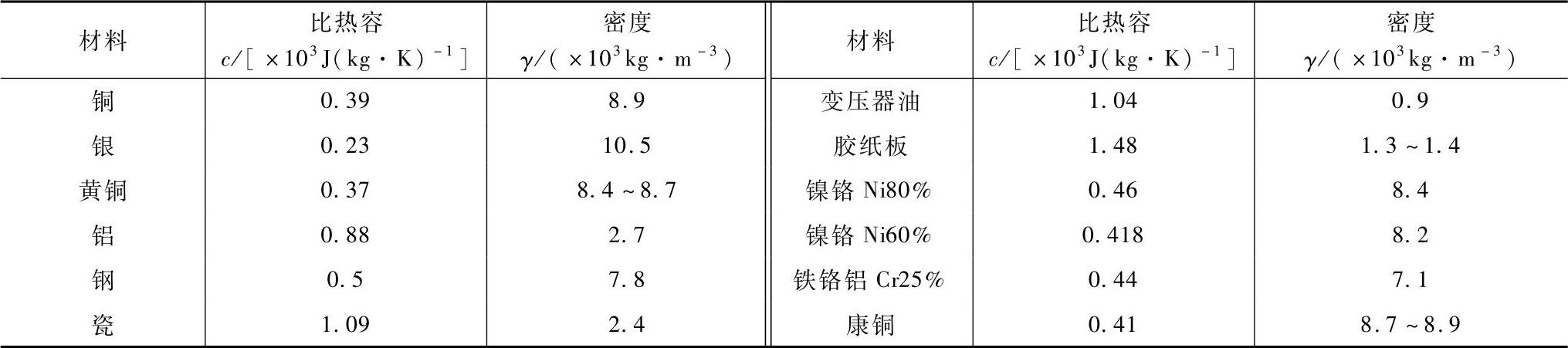
对于图4-159所示的长为l，截面积为A的导体

式中 R——导体电阻（Ω）；

ρ——导体电阻率（Ω·m）；

l——导体长度（m）；

A——导体截面积（m²）；

γ——导体密度（kg/m³）。

导体电阻率可用下式计算：

ρ=ρ₀（1+αθ） （4-168）

式中 α——电阻温度系数；

θ——导体温度（℃）；

ρ₀——0℃时导体的电阻率。

对于交变电流应考虑交流附加损耗系数K。(www.xing528.com)

将式（4-165）～式（4-168）代入式（4-164）得

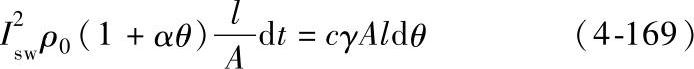
即 。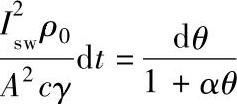

在t=0到t=t_sw的时间范围内，温度由θ=θ₀到θ=θ_sw的条件下进行积分，即

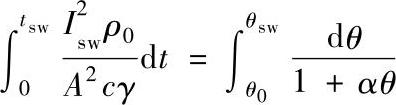
解之得

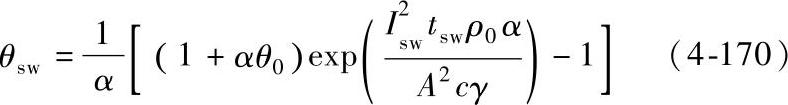
式中 θ₀——起始温度，是周围环境温度与额定电流下的稳定温升之和。

电器的热稳定性以热稳定电流I_sw的二次方与热稳定时间的乘积，即I²_swt_sw来表示。由式（4-170）可以求出载流导体在允许发热温度θ_sw下的热稳定公式为

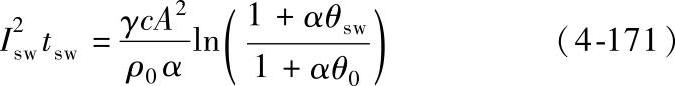
在给定t_sw、I_sw和θ_sw条件下，导体截面积可由下式决定：

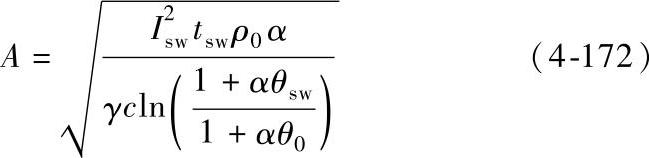
如果给定A、θ_sw和t_sw，则允许的热稳定电流为

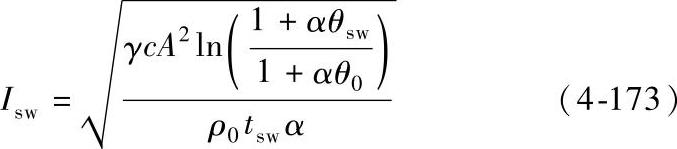
当给定A、θ_sw和I_sw，则允许的热稳定时间可按下式求得

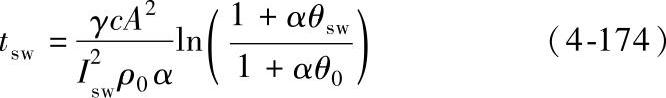
热稳定时间（额定短路持续时间）通常取1s、2s与4s。

短路时允许的电流密度为

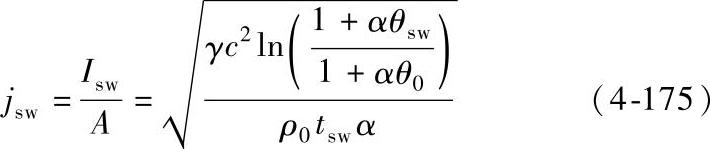
由式（4-171）可知，热稳定电流I_sw的二次方与热稳定时间t_sw的乘积I²_swt_sw为一常数，因而可得出下面关系式为

根据式（4-176）可将时间为t_sw1的热稳定电流I_sw1换算到时间为t_sw2的热稳定电流I_sw2。

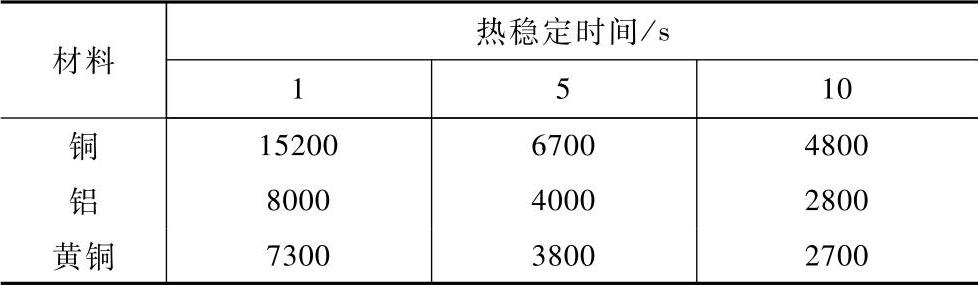
表4-27给出了不同材料在不同的t_sw值时允许电流密度的经验值。

表4-27 短路状态下允许的电流密度 （单位：A/cm²）