如何缓解长期工作引起的发热问题？

1.发热的计算

有些电器，比如断路器在其服役期间的绝大多数时间里都处于闭合状态，导通额定电流，此时的电器处于长期工作制下，其工作时间通常大于8h，可以达到几天，甚至几个月。

下面分析以一个放置在空气中的载流长导体为例来说明长期工作制下的升温过程，如图4-154所示。

在t=0以前，导体内无电流，导体温度θ与周围介质温度θ₀相同。在t=0以后，导体通过电流I，产生功率损耗使导体温度升高。导体温度升高后，θ＞θ₀，将有热量传到周围介质中去。根据能量平衡原理，在dt时间内，导体各能量之间的关系可用下式表示：

dQ=dQ₁+dQ₂ （4-156）

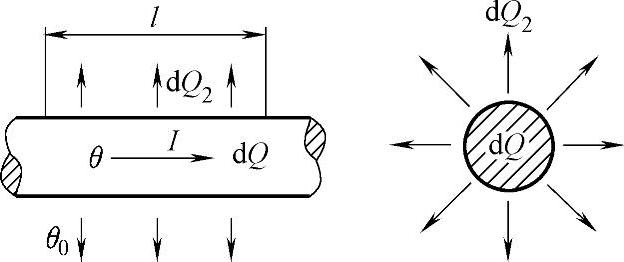
图4-154 导体的升温

式中 dQ——导体在dt时间内产生的损耗热量；

dQ₁——导体在dt时间内升温所需的热量；

dQ₂——导体在dt时间内传到周围介质中的热量。

由式（4-156）得

式中 Φ——热流量，按常数考虑；

C_t——导体热容量；

R_t——导体热阻；

τ——导体温升，τ=θ-θ₀。

整理式（4-157）得

解式（4-158）得

取 τ_s=ΦR_t （4-160）

T_t=C_tR_t （4-161）

式中 τ_s——稳定温升（K）；(www.xing528.com)

T_t——热时间常数（s）。

将式（4-160）、式（4-161）代入式（4-159）中，得

由式（4-162）可得导体温升τ的变化曲线如图4-155所示，也可将数据列于表4-25。

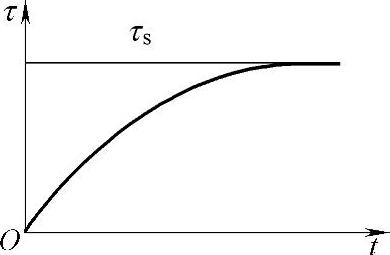
图4-155 导体发热温升变化曲线

表4-25 温升曲线表

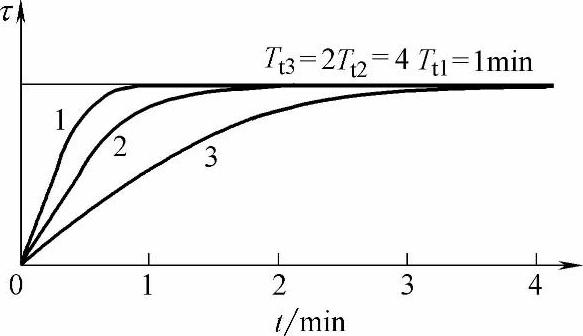
图4-156 不同热时间常数T_t的发热过程

2.热时间常数

从图4-155和表4-25可以看出从导体开始通电到发热基本稳定所需的时间只决定于时间常数。热时间常数T_t对发热过程的影响如图4-156所示。热时间常数越大达到稳定温升的时间越长。

对于放在空气中的裸导体，T_t可写成

由式（4-163）可以看出导体的比热容c和重量G越大，T_t越大；表面散热系数K及表面积S越大，T_t越小。

3.稳定温升分布示例

外包绝缘层的圆导体，绝缘层内径为r₁，外径为r₂，导体稳态发热温度为θ₁，绝缘层外表面温度为θ₂，周围空气温度为θ₀，则其稳态温升分布如图4-157所示，

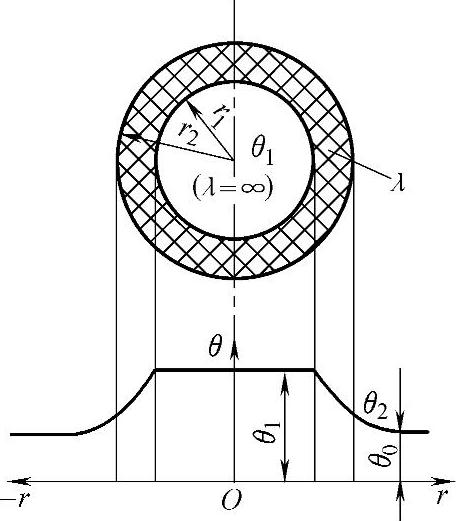
图4-157 外包绝缘层的圆截面导体的热传导

对图4-158a所示的变截面形状导体，其中l₁长的一段具有狭窄的截面A₁，在达到稳态时沿导体轴向温升分布为一指数曲线，如图4-158b所示。

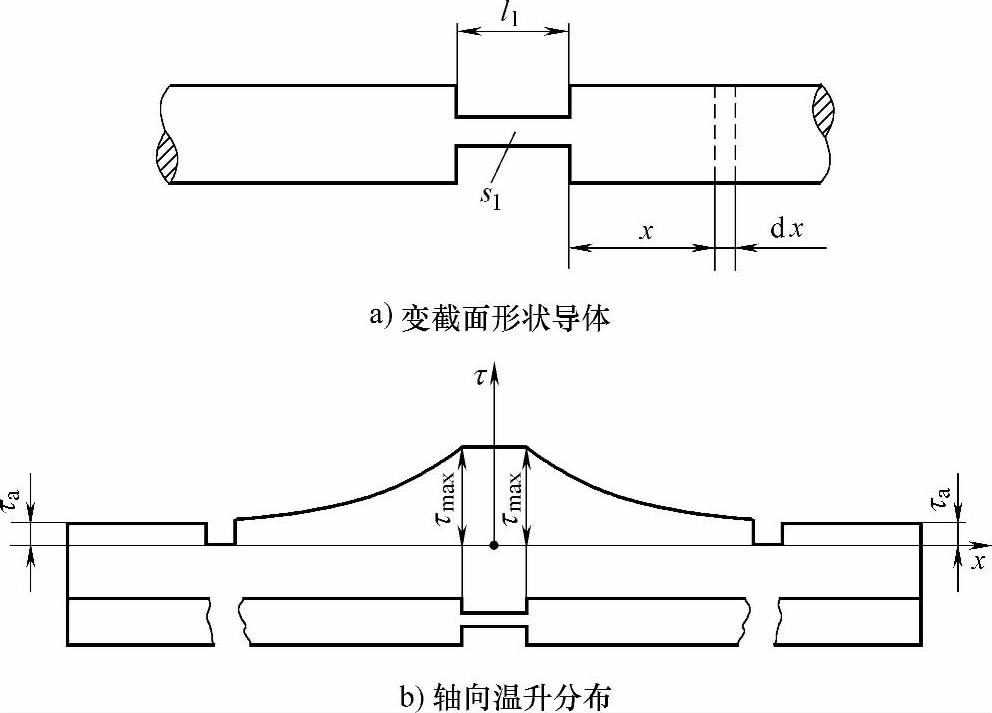
图4-158 具有狭窄部分的变截面形状导体及其轴向温升分布