触头熔焊力测量与影响因素分析

所有的触头都会在某种程度上发生熔焊或粘连，只有当熔焊使触头不能正常打开时这个问题才突出出来。熔焊的形成过程是电路电流（无论燃弧与否）、触头材料、触头表面情况、触头表面膜的特性以及开关机构的一个复杂函数。熔焊力可由下式给出

F_w=ΓA_w （4-125）

式中 Γ——触头材料的抗拉强度；

A_w——熔焊面积。

Γ≈H/3，H是材料的硬度，因此

F_w=HA_w/3 （4-126）

材料的抗拉强度不是一个具体的数值，通常它是一个范围，见表4-16。因此我们可以知道即使是式（4-125）和式（4-126）这样简单的方程，无论是对任何一个触头来说测量到的熔焊力差异都会很大。

图4-134 电弧弧根处的磨损及需要的触头尺寸

表4-16 材料的硬度和抗拉强度

触头熔焊既能在触头处于闭合状态下通过大电流时产生，也能在触头关合时由预击穿电弧产生，触头熔焊还会在触头弹跳产生的电弧作用下被加强。

1.触头闭合状态下的熔焊

如果假设当接触面积达到熔化温度T_m时发生熔焊，由式（4-43）可知当触头熔焊时闭合触头之间的电压为

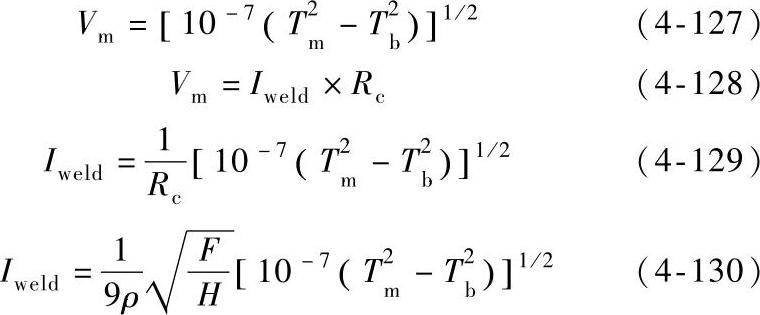
式中 ρ——电阻率（Ω·m）；

H——硬度（N·mm^-2）；

F——触头压力（N）。

式（4-130）还可进一步用于分析材料参数受温度的影响的情况。

对于一个给定的触头压力F有一个与之对应的触头熔化电流，因此式（4-129）只能用于触头闭合力远远大于触头斥力的情况。用下面这个方程可以方便地得到使平板触头保持良好接触而不发生熔焊的触头压力F_s（N）保守估计值：

F_s=8×10^-5I^1.54 （4-131）

图4-135给出了多种触头材料的熔焊临界电流值，图中还可以看出在一个给定电流下熔焊力F_W的差异是相当大的。因此，研究者们通常把给定电路参数和接触条件下的熔焊力数据用累积概率方法来表示，如图4-136所示。

通过一些简单的假设有可能估计出最大熔焊力。让我们来看图4-137，假设金属熔化区为球形，球的半径为a，熔焊区域A_w的半径也为a。

另外，还假设这个球形金属熔化区被熔焊电流绝热加热，则熔化这个接触区域的能量W_c为

W_c=m[c_V（T_m-T_b）+C_L] （4-132）

式中 m——熔化金属的质量；

c_V——比定容热容；

T_m——熔化温度；

T_b——初始温度；

C_L——熔化潜热。

材料的密度为δ，有

假定熔焊区域就是球形金属熔化区的横截面，有A_w=πa²，熔焊力F_w为

F_w=Γπa² （4-135）

由方程（4-134）和式（4-135），消去a，可得

F_w=KW^2/3_c （4-136）

式中

如果所有的能量都用来熔化接触斑点，则有(www.xing528.com)

式中 V_c——接触压降。

这样由式（4-136）和式（4-138）可以得到预期的最大熔焊力，不同触头材料的熔焊力理论极限值为

银：F_w=67W^2/3_c

铜：F_w=127W^2/3_c

图4-138示出触头材料为铜的情况，由图中可以看出只有几个测量值超过理论曲线，而且其误差不超过30%，而这是在熔化区域上作很大简化的基础上得到的。

如果触头保持力小于触头斥开力，触头间会产生电弧。此时式（4-138）中的电压为电弧电压U_A，输入接触区域的总能量将是

时间t_c是触头闭合状态的时间，t_a是触头间的燃弧时间。

2.触头关合时产生的熔焊

我们在4.3.1节中讨论过触头关合过程中会产生电弧，一旦形成了电弧，电弧就会使触头表面熔化。因此，当触头接触后，处于熔融态的金属会冷却凝结形成熔焊。实际上对大多数开关装置来说预击穿电弧持续的时间很短，形成的熔焊也非常微弱。但是一旦触头闭合后产生弹跳熔焊就会变得严重得多。触头弹跳的程度取决于触头材料、开关的设计以及动触头关合时的动能。

图4-135 闭合触头的熔焊临界电流值以及给定电流下熔焊力测量值的差异

a）硬银 b）Ag/Ni10 c）Ag/Ni20 d）W/Ag60 e）Ag/CdO13内氧化 f）Ag/C3

图4-136 AgW触头熔焊力的累积概率

图4-137 熔焊区域和假定的球形熔化区

为了估计最大熔焊强度，我们仍可使用式（4-136），

即

F_w=KW^2/3_c （4-140）

电弧在两个距离很近的触头间燃炽时，

式中 U_A——电弧电压；

t_a——燃弧时间。

通常测量到的熔焊力比式（4-140）中给出的计算值小，可能有这样一些原因：当电弧弧根在触头表面上运动时，两个触头上的熔斑并不一定严格对应，因此当触头接触后，熔焊面积A_w没有理论预测值大。另外，当燃弧时间t_a足够大时，对接触区域的加热就不再满足绝热条件，因此4.10.4节描述的热平衡就开始起作用了。当电弧较长时，并不是所有的能量都用来加热触头弧根斑点。因为在一次合闸过程中触头会合分若干次，因此触头的弹跳时间估计起来有点复杂，这样对最终熔化区域影响密切的t_a值不易确定。最后，触头接触面的情况与触头基体材料可能不同，比如触头是一合金材料，在电弧烧蚀后的触头表面组分就可能与触头基体材料不同了，这样熔化温度就可能产生明显变化。还应指出燃弧后的触头表面可能生成氧化物或其它化合物，这也会影响熔焊强度。图4-139示出对于一个已氧化的AgCdO触头可能产生的熔焊强度，在实验中触头弹跳时间被精确控制，仅允许产生一次弹跳电弧。图中最大熔焊力满足关系

F_w=7.6W^2/3_c （4-142）

其形式与式（4-136）相同，但是在这种情况下常数K=7.6，而如果通过式（4-137）计算纯银的K值，K=67。图4-139中的K值与理论值在数量级上的差异告诉我们不能把纯金属的数据代入到合金中，在合金中添加的组元有可能减小熔焊力。图4-140示出了在一恒定弹跳时间下不同触头材料的熔焊强度有很大的不同。

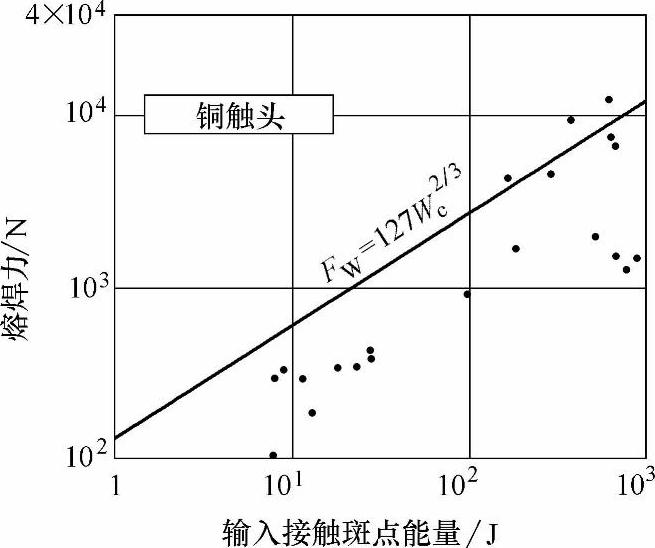
图4-138 触头为铜时预期的最大熔焊力与输入接触斑点能量的函数关系

图4-139 AgCdO（其中CdO质量比为10%）触头的最大熔焊力与电弧能量的关系

图4-140 相同触头弹跳时间下不同触头材料熔焊力的对比（控制触头弹跳只有一次）

a—CuPd（40/60） b—Pt（flat） c—Pt（domed） d—Ag-Ni e—Cu f—Ag-Pd（40/60） g—Ag（domed） h—Ag-W（50/50） i—Cu-Ag j—Te-Cu（0.5/99.5） k—Ag-Mo l—Ag-Wc m—Ag-W（50/50）Ag-C n—Ag-CdO（90/10）

注：Kleine的结果（Ⅰ）银-镍（Ⅱ）银（Ⅲ）银-石墨15/65（Ⅳ）银-氧化镉90/10（400A）。