当流过收缩斑点的电流足够小，产生的热效应对接触电阻的影响忽略不计时，收缩电阻的定义ρ/（2a）是有效的。在这样的条件下，当一个电流I流过收缩处产生的电压降就是ρI/（2a）。当收缩斑点处的焦耳加热足够大时，汇聚在接触斑点处电流线就会产生与电流收缩相垂直的热梯度。这个梯度使得接触电压降与电流以及a斑点尺寸之间的关系变得复杂起来。以下就为本节所要讨论的这个关系。
当a斑点流过电流时，其温度很快上升到一个平衡温度。比如说，我们考虑在两个电阻率为ρ，热导率为λ的半无限大的导体之间有一个半径为a的圆形斑点，如果ρ和λ与温度无关，那么用球坐标描述在收缩处的温升的微分方程为
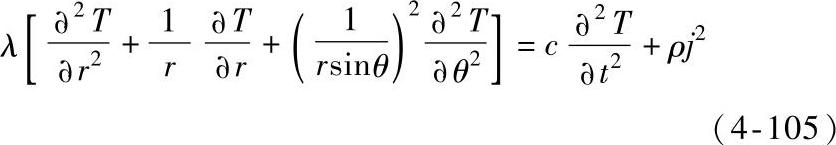
式中 j——位置（r，θ）处的电流密度；
c——单位体积的热容量。
该方程只能通过数值方法求解，但是方程的解可用下述形式的因子叠加表示：
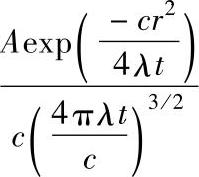
因此距离收缩中心点r≈a处温度上升的时间常数为ca2/（4λ）。对金属导体，室温下的铜的λ和c的值为400W·m-1℃-1和3.44×106J·m-3℃-1，铝的λ和c的值为236W·m-1℃-1和2.43×106J·m-3℃-1。因此，对于一个收缩半径为10μm的a斑点铜和铝的时间常数分别为2.2×10-7s和2.6×10-7s，这个时间常数随收缩半径的减小而迅速减小。Holm计算出了两个半无限大导体之间的半径为a的圆形斑点的温度随时间的变化规律以及温度的空间分布，示于图4-124中。随着a斑点的加热其温度上升时间很短，因此在静态接触或缓慢移动接触场合热的瞬态过程可以忽略不计，在这种情况下只有平衡态温度才是我们感兴趣的。热的瞬态过程仅仅在快速移动的电接触如电刷接触，或高频大功率电接触情况下才需要考虑。我们在此只考虑处于热稳态下的电接触。
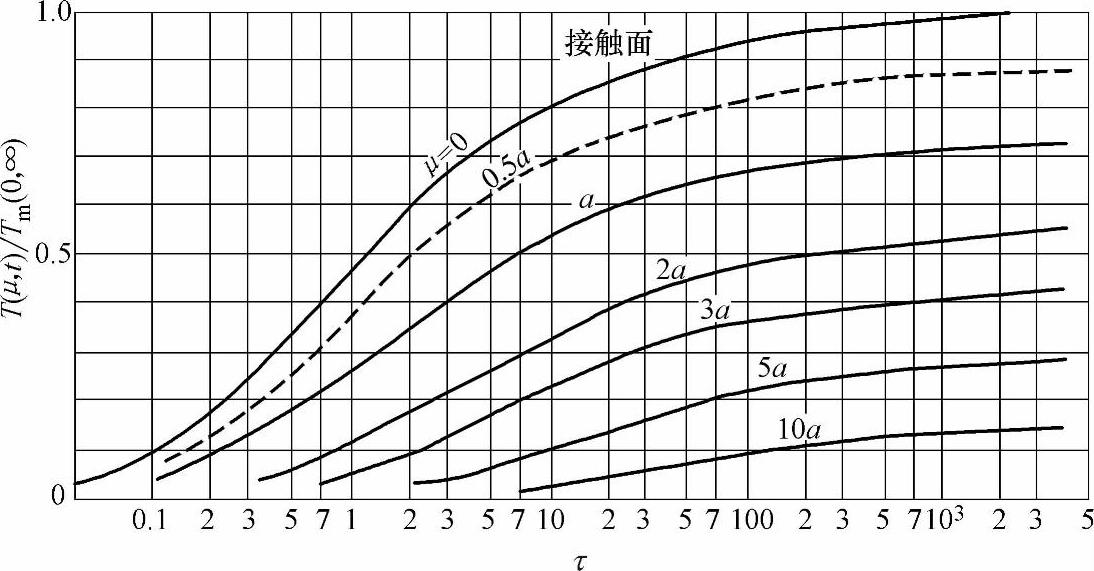
图4-124 标么值温度（稳态温度Tm作为基准值）与标么值时间τ的关系
图4-124中，标幺值时间为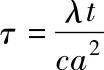
式中 λ——热导率；
c——单位体积热容；
a——a斑点半径。
参数μ是在接触导体内以收缩斑点中心为圆心，沿收缩圆柱轴线方向等热面的位置。远离收缩点处的导体温度取0℃。
1.接触电压与温度的关系
处理热平衡下的电接触问题时通常是假定导体的外表面与外部环境是绝热的，在a斑点中产生的热仅仅在导体内传播。在这样的条件下，电流线和热流线重合，等位面和等热面重合。电流和热流之间相对应使得Kohlrausch推导出接触斑点上电压降V和接触面上最高温度Tm之间的一个简单关系
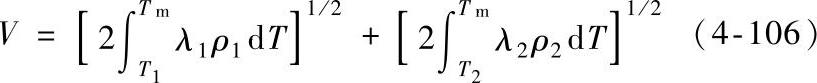
式中 λ和ρ——分别是导体的热导率和电阻率；
下标1和2——分别指接触的两个导体；
T1和T2——分别是两个导体中远离收缩区处的导体温度。
λ和ρ一般随温度变化。因为大部分电流线都通过a斑点，最高温度Tm一定会出现在a斑点的范围内或就在a斑点的邻近区域。对于同一种金属相互接触的情况，λ1=λ2=λ，ρ1=ρ2=ρ，Tm位于a斑点中，此时
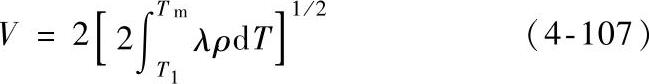
在一定的温度范围内λ和ρ随温度的变化很小，由式（4-107）即可推出我们熟知的电压-温度关系
式（4-108）的左端项（Tm-T1）是a斑点温度与远离收缩区处导体温度之差，叫做接触超温。式（4-108）广泛见于各种电接触文献中，并且在工程中用来评估电连接在工作状态下的超温。一般来说电连接在极限工作状态下的超温不超过1～3℃。在超温达到几十摄氏度时，式（4-108）已无法使用了，因为它是在材料的电阻率和热导率都是常数的基础上推出的，正如前面所提到的，ρ和λ都是随温度变化的，此时的V-T之间的关系将在下面阐述。
在推导更高接触温度下的V-T关系之前，我们有必要观察一下式（4-106）～式（4-108）的右端项，其中的材料参数只包括λ和ρ，而与触头几何形状无关。因此V-T关系适用于任何形状和任意尺寸的触头。由数学推导可以看出得到的V-T关系适用于任何传导电流且与外界绝热的导体，我们可由下面一个简单的例子说明。
一个等直径导电金属棒长度为2L，横截面为A，通过一个均匀的电流，电流密度为j，如图4-125所示。棒两端的温度都为T0。如果导体与周围环境是绝热的，其内部的温度分布T（x）由下面的微分方程决定：
式中 λ和ρ——分别是导体棒的热导率和电阻率；
x——棒轴线上的距离。
如果为了简单起见假设λ和ρ与温度无关，式（4-109）的解为
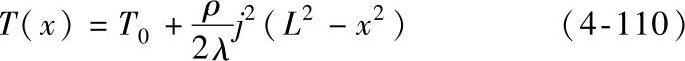
最高温度显然出现在x=0处，即导体棒的中间位置。因为导体棒上的电压降为
V=2ρjL （4-111）
导体棒的最高温度与棒两端的温度差，即超温则为
T（0）-T0=V2/（8ρλ） （4-112）
这与式（4-108）相同。由此可以看出式（4-108）以及更通用的式（4-106）适用于任何一个被电流加热且与外界绝热的导体。
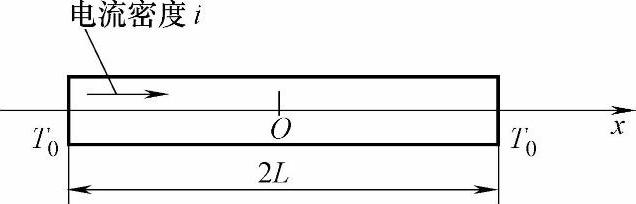
图4-125 一个横截面均匀的导电棒被电流密度为j的电流加热
2.材料的电阻率和热导率随温度变化情况下对接触电压与温度关系的影响
通常热导率和电阻率在一个很宽的温度范围内随温度变化的关系可表达为λ=λ0（1-βT），ρ=ρ0（1+αT），其中下标0指的是在0℃的值，β和α分别是热导率和电阻率的温度系数。金属的热导率一般随温度的增加而减小，而电阻率增加。将此关系代入式（4-106）中可以得到如下的V-T关系
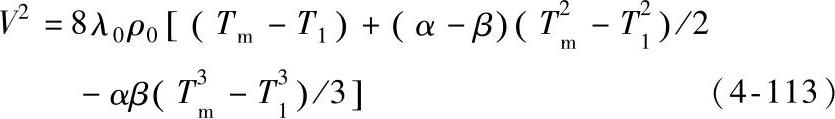(www.xing528.com)
一些常见金属的电接触如铝-铝，铜-铜，黄铜-黄铜接触的Tm与V的关系示于图4-126中。而铝-铜曲线位于曲线1，2之间，铜-黄铜曲线位于曲线1，3之间，铝-黄铜曲线位于曲线2，3之间。由图中可以看出当接触电压仅仅超过10mV时接触温度就超过远离收缩区处的导体温度了。当接触电压超过0.1V时接触温度就能使触头材料软化或熔化。表4-14给出了在式（4-113）基础上计算得到的常见电接触材料的软化电压和熔化电压。Timsit实验研究了V-T关系的应用范围，研究发现只要a斑点的平均直径大于接触导体中电子的平均自由程这个关系就成立。
3.魏德曼弗朗兹定律
式（4-113）是V-T关系的准确表达式。在一个较宽的温度范围内，材料的电阻率和热导率与温度呈线性关系，式（4-113）成立。
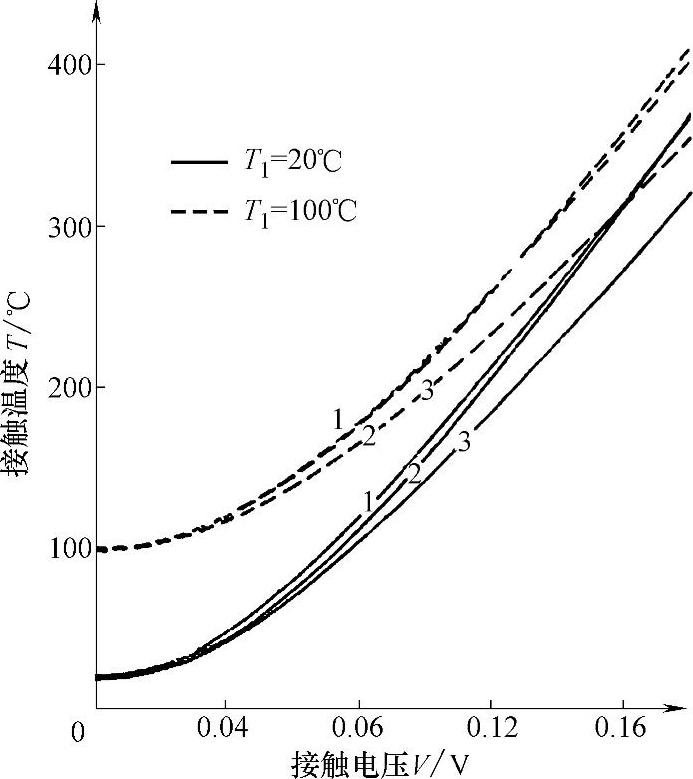
图4-126 电接触的接触电压与温度之间的关系，远离收缩区处的导体温度T1分别为20℃和100℃
曲线1—铜-铜 曲线2—铝-铝 曲线3—黄铜-黄铜
表4-14 常见电接触材料的软化电压Vs和熔化电压Vm
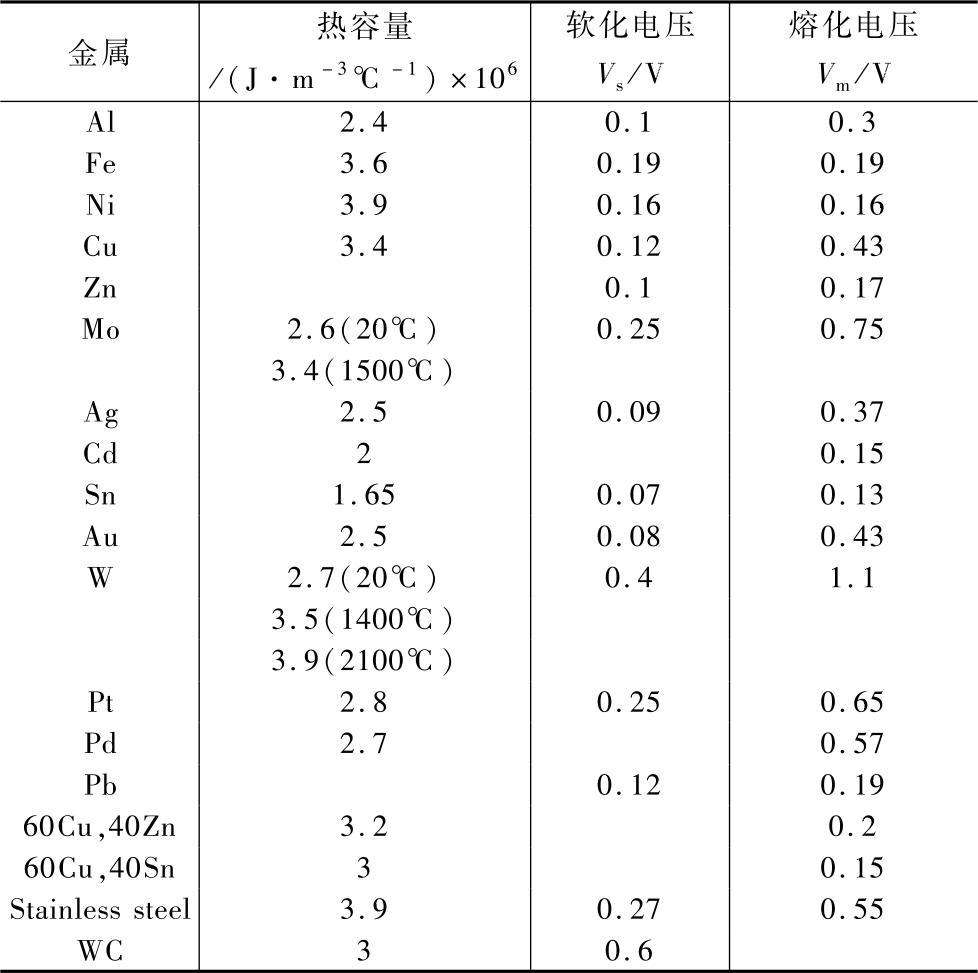
由图4-126可以看出，在远离收缩区处的导体温度相同时，所有曲线都非常接近，还可以证明许多金属的V-T曲线也与这些曲线非常接近。这个有趣的现象在一定程度上归因于魏德曼弗朗兹定律（Wiedemann-Franz law），它告诉我们金属的热导率和电阻率随温度的变化满足如下关系
λρ=LT （4-114）
式中 L——洛仑兹常数（2.45×10-8V2K-2）；
T——绝对温度。
只要金属的热导率和电阻率是由电子传输过程所决定式（4-114）即成立，因此在常见的电接触温度范围内这个关系都能够很好地描述金属的热传输特性和电传输特性，但是在这个范围之外它就不适用了。如果式（4-114）成立，可以导出V-T的严格表达式
V2=4L（T2m-T21） （4-115）
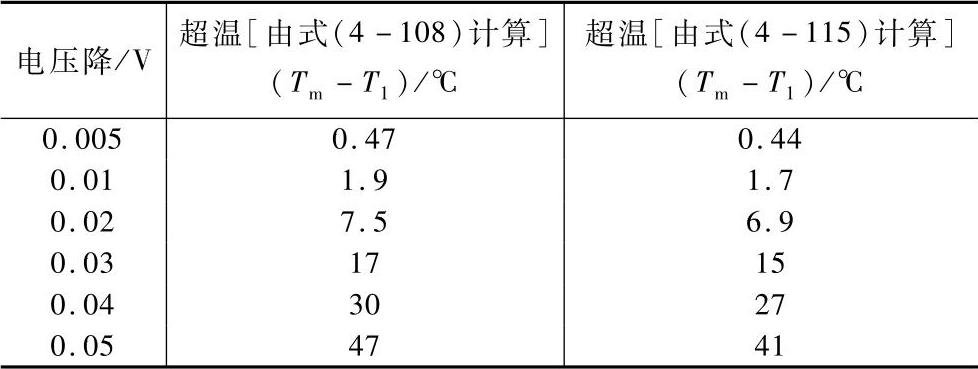
式（4-115）与触头材料无关。式（4-115）虽然准确，但是使用起来不如式（4-108）方便，因为它无法直接由接触压降得到超温（Tm-T1）。我们可以在电接触中常见的接触压降V下将式（4-108）得到的超温和由式（4-115）得到的更准确的超温进行一下比较，比如我们考虑铜-铜接触，收缩区外导体温度T1为20℃，室温下铜的电阻率和热导率分别为1.75×10-8Ω·m和380W·m-1℃-1，代入式（4-108）中。在不同的接触压降V下由式（4-108）得到的超温和由式（4-115）得到的更准确的超温比较结果示于表4-15中，由表中可以看出在接触压降不超过0.05V时从工程的角度看它们的差别很小，从而人们更常用式（4-108）来估计电接触中的超温。
从式（4-115）还可推导出式（4-108）。我们定义接触中的平均超温Tav等于（Tm+T1）/2，由式（4-114）可得
λavρav=L（Tm+T1）/2 （4-116）
因为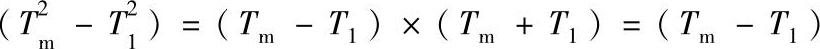
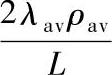，将其代入式（4-115）中可得
Tm-T1=V2/（8λavρav） （4-117）
因此当物理参数λ和ρ取平均温度下的值时即可由式（4-115）推导出式（4-108）。
表4-15 式（4-108）和式（4-115）得到的超温结果比较
4.a斑点附近的温度分布
计算a斑点的温度分布可利用导体中的等位面和等热面重合的特性。Greenwood和Williamson指出最高接触温度Tm与流过的电流I之间满足如下关系：
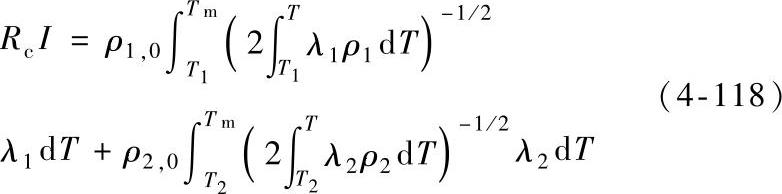
式中 T1和T2——分别是材料1和材料2的远离收缩区处的导体温度；
Rc——“冷态”接触电阻；
ρ1，0和ρ2，0——分别是材料1和材料2的“冷态”电阻率，材料的电阻率与温度相关，ρ=ρ0（1+αT）；
λ1和λ2——分别是材料1和材料2的热导率，热导率与温度的关系λ=λ0（1-βT）。
因为RcI是“冷态”接触压降，因此从式（4-118）可知接触头的最高温度与电流通过“冷态”接触头产生的压降有关。因此式（4-118）中的积分为
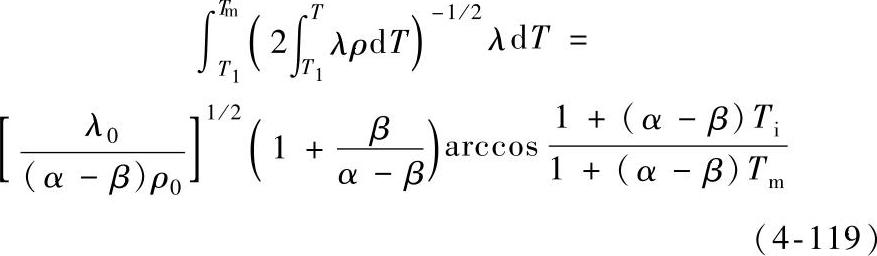
对于同一种金属相互接触，收缩区外导体温度T1=T2=0℃的情况，Rc=ρ0/（2a），因此式（4-118）变为
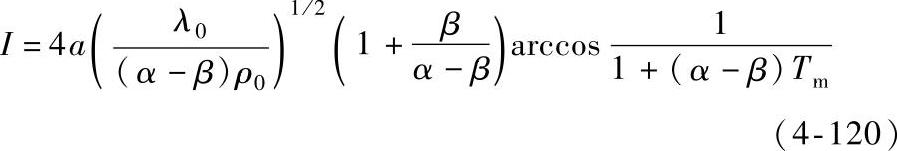
由式（4-78）可知在轴向上距离收缩中心点为μ的等位面之间所包含的电阻为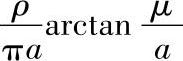
，因此式（4-118）可变为
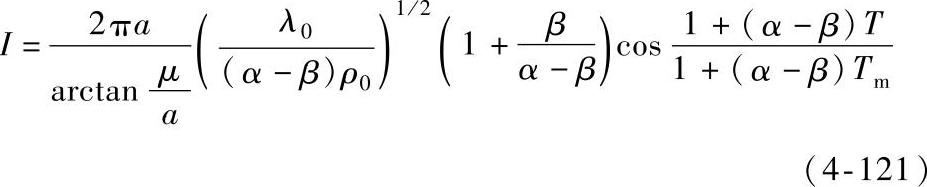
联立式（4-120）和式（4-121）可得在轴向上距离收缩中心点为μ的等位面上的温度满足：
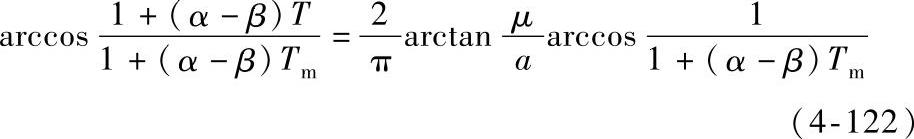
在收缩面垂直方向上以及接触面上的温度分布如图4-127所示，计算条件是β=0℃-1，α=4×10-3℃-1，Tm=1000℃。由图中可以看出在几个收缩斑点直径的距离外其温度就已经下降到了远离收缩区处的导体温度了。
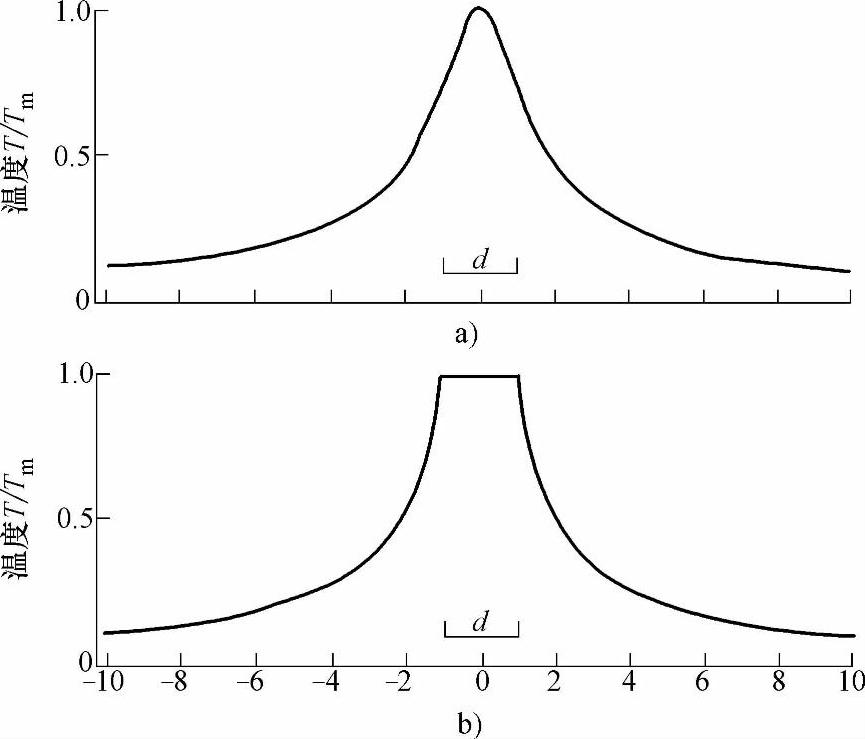
图4-127 导体中稳态温度分布（热导率为常数，电阻率与温度呈线性关系ρ0（1+αT），α=4×10-3℃-1，Tm=1000℃，d为收缩斑点直径2a）
a）沿收缩圆柱轴向上的温度分布（横坐标—与收缩面的垂直距离，z/a） b）在接触面上的温度分布（横坐标—收缩平面内距收缩中心处的径向距离r/a）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
