收缩电阻测量与计算比较及形状因子的影响分析

为了简单起见，在收缩电阻的分析过程中一般都假定a斑点是圆形的。大多数的电接触问题都可以用圆形a斑点描述，但是为了问题的完整性起见，也会讨论其它形状的a斑点。

1.圆形a斑点

处于两个半无限大导体之间的一个圆形a斑点如图4-104所示，两个导体中的等位面为一椭球面，其形状由如下方程确定：

式中 μ——一个参数；

r和z——圆柱坐标。

在纵轴上高度为μ的等位面之间所包含部分的电阻由下式给出

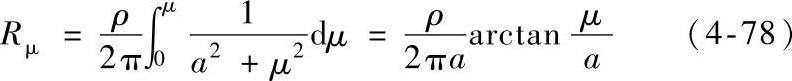
式中 ρ——导体的电阻率。

当μ很大，即距离收缩处足够远时，可得一个接触导体的收缩电阻或分布电阻为

两个导体的总收缩电阻是其两倍：

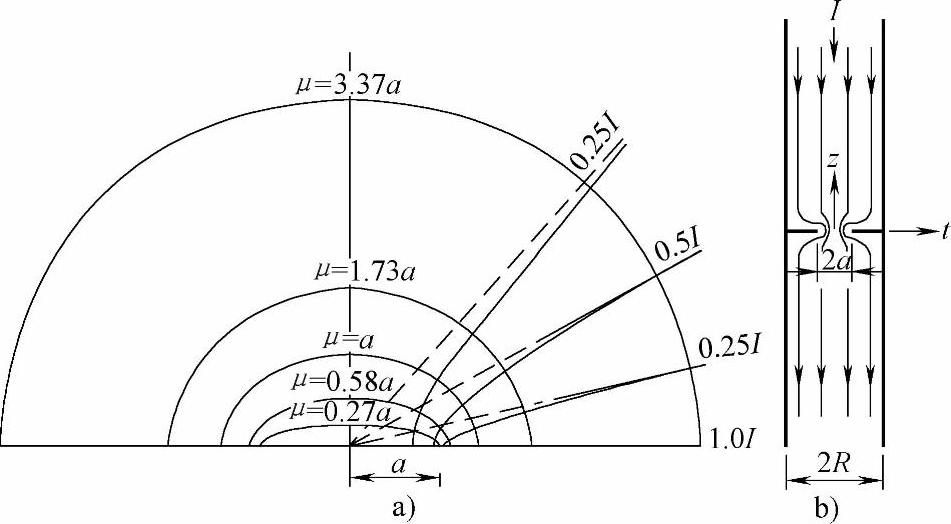
图4-104 两个半无限大导体之间的一个圆形斑点

a）电流收缩处附近的等位面和电流线分布，μ为纵轴参数，电流线标出了电流分布 b）电流通过两个半径为R的圆柱形

导体时在半径为a的圆形斑点处收缩的情况

收缩电阻表达式（4-79）和式（4-80）广泛地见于各种电接触相关的文献以及电接触相关的设计中。在本章中还将给出式（4-80）的广义表达式，它可用于非圆形a斑点的情况。如果两个接触导体的电阻率不同，分别为ρ₁和ρ₂，那么每一侧的收缩电阻为ρ_i/（4a），i=1，2。那么总收缩电阻为

在此我们用铜导体与铜导体之间的电接触来估计一下a斑点的半径对收缩电阻的影响，接触斑点为圆形a斑点，铜的电阻率为ρ=1.75×10^-8Ωm，结果示于表4-10中。

表4-10 铜导体与铜导体接触的收缩电阻（圆形a斑点）

从表中可以看出当收缩半径为10μm时收缩电阻约为1mΩ，这是一个非常低的电阻值，事实上当20A电流通过这个收缩点时都不会引起过热。如果收缩半径达到100μm时通过200A的电流也不会引起过热。由此可以看出，当两个导体相互接触导电时并不需要两个接触面之间有很大的导电面积就可以得到满意的低接触电阻了。

如图4-104b所示的两个半径为R的圆柱形导体相接触且接触面为圆形a斑点的情形，可以用拉普拉斯方程结合合适的边界条件求解出收缩电阻R_c。其准确表达式为

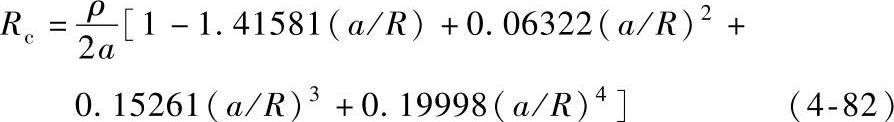
当收缩半径a比导体半径R小得多时，式（4-82）可简化为式（4-80）。图4-105示出收缩电阻R_c的测量值与计算值的比较，测量值与计算值的之间相符很好，说明式（4-82）是适用的。

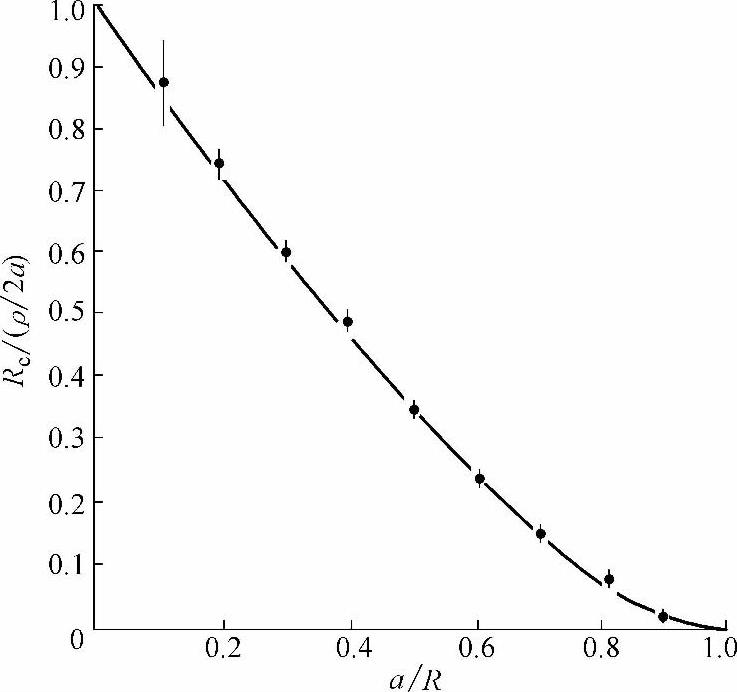
图4-105 半径为R的圆柱形导体相接触且接触面为半径为a的圆形时，在不同的a/R下， 收缩电阻测量值和计算值的比较

当圆柱形母线相互连接承载大电流时，接触半径一个很小的变化就会引起收缩电阻很大的变化，这会对功率损耗产生显著的影响。在其收缩处的电流密度分布如下式所示

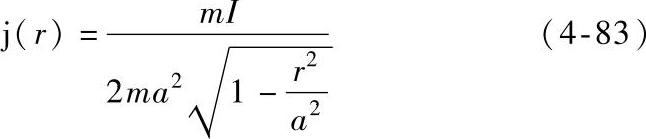
式中 I——电流；

r——径向位置；

m——系数（一般为1，只有a/R大于0.5时m才会不等于1）。

2.非圆形a斑点和环形a斑点

当接触面的微观几何拓扑不是各向同性时，就不能把a斑点假设为圆形。在这一节中让我们来看一看当接触面形状偏离圆形时对收缩电阻有怎样的影响。

霍尔姆告诉我们当接触面为长半轴为a，短半轴为b的椭圆形时，其收缩电阻R_c（a，b）为

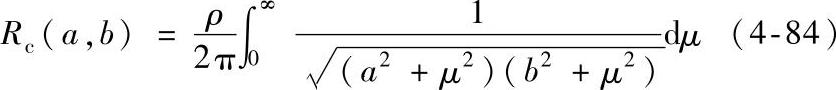
它还可以表示为

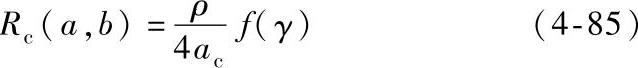
式中 ；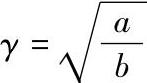

f（γ）——函数是一个形状因子；

a_c——与椭圆面积相等的圆半径。

形状因子f（γ）与γ的关系示于图4-106中，当γ从1增加到无穷时，即接触斑点变得越来越长时，形状因子从1减小到0。注意当γ从1增加到10左右时，收缩电阻下降得比较缓慢。两个半无限大的导体以椭圆形a斑点接触时收缩电阻为2R_c（a，b）。

图4-106 形状因子f（γ）随γ的变化关系

Aichi和Tahara用电解槽测量了矩形a斑点的收缩电阻，结果示于图4-107中。对图中的数据进行回归分析得到的收缩电阻R_c经验公式为

式中 S——矩形面积，矩形的长宽比为10以上；

k——一个与收缩情况相关的参数，当矩形宽度从1mm增加到10mm时k在0.36到1之间变化（S的单位为mm²，ρ的单位为Ω·mm）。

两个半无限大的导体以矩形a斑点的形式接触时收缩电阻为2R_c。式（4-86）还可以表示为

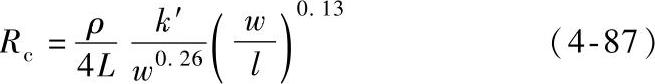
式中 w和l——分别是矩形的宽度和长度；

L——与矩形面积相等的正方形宽度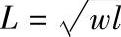，；k′=4k。(www.xing528.com)

公式（4-87）与公式（4-85）一样都是广义形式的表达式，并且与公式（4-85）一样，当长宽比l/w增加时收缩电阻缓慢减小。当长宽比大于10时，公式（4-85）与公式（4-87）能得到非常相近的收缩电阻值。注意公式（4-87）不能用于长宽比远小于10的情况。

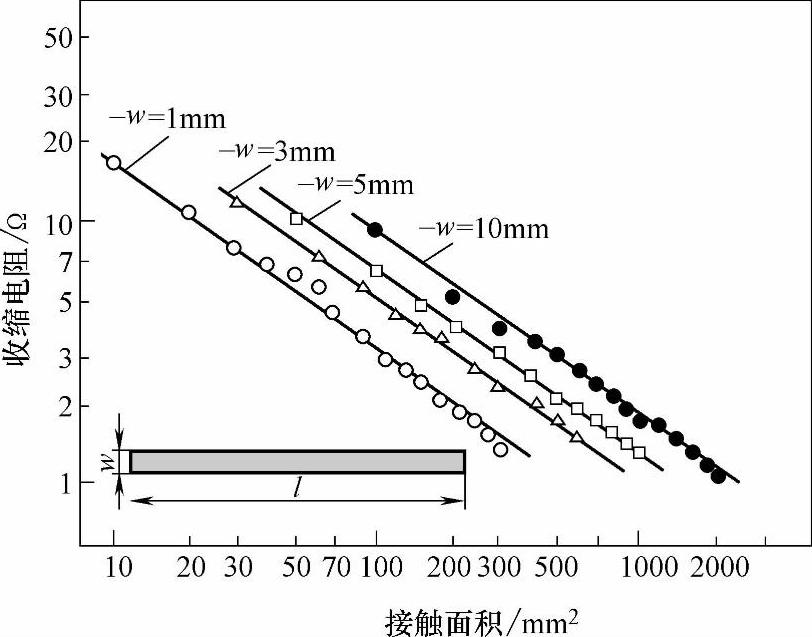
图4-107 矩形a斑点收缩电阻与矩形面积的关系矩形宽度为w，长度为l。电解槽中电解液的电阻率为175Ωmm

Nakamura对正方形a斑点，以及圆环形和方环形a斑点的收缩电阻进行了严格地推导，得到两个半无限大的导体之间形成的边长为2L的正方形a斑点的接触电阻为

R_c=0.434r/L （4-88）

请注意这个表达式得到的收缩电阻值比圆形a斑点的接触电阻值0.25ρ/a大70%左右。圆环形和方环形a斑点的收缩电阻如图4-108所示，其表达式为

R_c=R₀F（ξ）-1 （4-89）

式中 R₀——实心圆形a斑点或正方形a斑点的收缩电阻；

F（ξ）——形状因子（在圆环形a斑点的情况下ξ=t/a，其中t和a分别是圆环厚度和外径；在方环形a斑点的情况下ξ=t/L）。

从图4-108中可以看出圆环形a斑点和方环形a斑点的形状因子几乎一模一样，即收缩电阻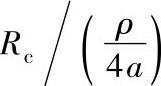与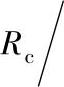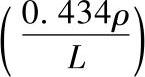之间的差别非常小。

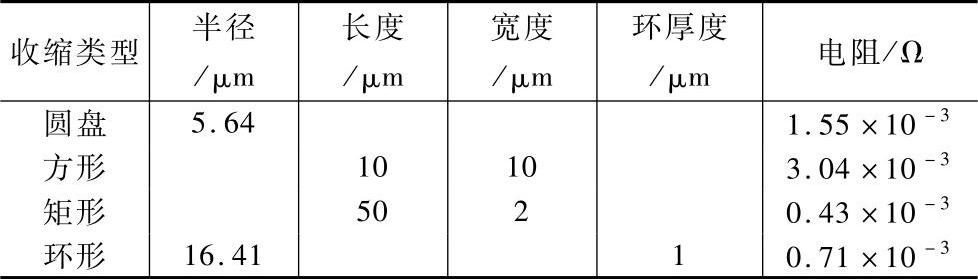
当接触表面为特殊结构时有可能出现矩形a斑点、圆环形a斑点和方环形a斑点，例如有一些电力系统中用的连接器，其表面有金字塔形的棱块可以嵌入导体中增加摩擦力，其a斑点就可能是正方形或矩形。环形a斑点是在硬块表面上再覆盖一层高导电材料，在这种情况下电流在通过收缩面时主要从棱块上的覆盖层中通过，此时就成为环形a斑点了。表4-11比较了在收缩面积同为100μm²时，铜与铜之间以不同形状的a斑点相接触时的收缩电阻，可以看出收缩电阻受a斑点形状的影响较大。

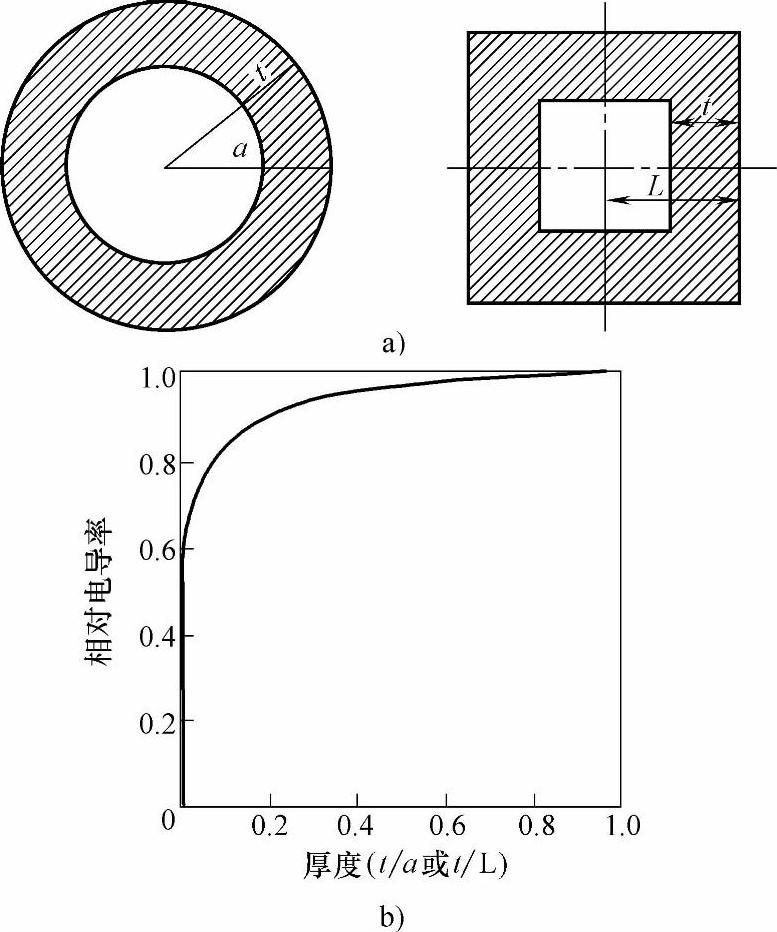
图4-108

a）圆环形和方环形a斑点 b）环形收缩形状因子F（ξ），圆环形a斑点的收缩电阻标么值表示为[ρ/4a]/R_c，方环形a斑点的收缩电阻标么值表示为[0.434ρ/L]/R_c，两条曲线的差别很小无法分辨

表4-11 收缩面积同为100μm²时，铜与铜之间以不同形状的a斑点相接触时的收缩电阻值

3.多个接触斑点

实际上电流从一个导体传导到另一个导体时不止经过一个a斑点，要经过多个a斑点。a斑点是由两个接触面上微观上的不平整形成的，这在图4-104中清楚地表明。Thomas和Probert在图4-109中示出微接触面的数量随接触压力的增加而增多，一个接触面是质地较软但表面光亮的钢表面，另一个接触面是经过喷砂工具处理的钢表面。接触斑点是在质地较软但表面光亮的钢表面上留下的印记。事实上两个名义平面之间的电接触是通过a斑点群来完成的。a斑点群的位置是由接触面上较大的波纹以及触头表面的微观拓扑所确定a斑点决定的。因此接触电阻既受a斑点数量和尺寸的影响，又受a斑点群的分布和尺寸的影响。虽然两个导体间在很多接触斑点处有接触，但是只有在表面绝缘膜如氧化膜破裂或剥离时接触斑点才成为导电的a斑点。因为氧化膜的破裂方式与接触位置微观接触处的变形模式有关，即弹性变形还是塑性变形，所以很难预测有多少斑点是导电的a斑点，但是我们知道它们比机械接触斑点的数量少得多。

为了方便进行计算，采用圆形a斑点来考虑金属与金属之间的多个a斑点的集体行为。在最简单的情况下，一个很大数量的n个圆形a斑点都处于一个a斑点群中，Greenwood的计算表明，在这种情况下下式能给出接触电阻的一个很好的近似值：

式中 a——a斑点的平均半径，定义为Σa_i/n（a_i为第i个斑点的半径）；

α——斑点群的半径，又叫做霍尔姆半径（Holmradi-us）。

图4-109 光学显微照片显示接触斑点的数量随压力的增加而增多

表4-12给出了当a斑点半径增加时式（4-90）中的二项大小的比较，这是由格林伍德（Greenwood）对图4-110所示76个相同的a斑点阵列得到的。在计算中，人为地斑点之间的距离取1个单位，a斑点的最大半径取0.5个单位。由表4-12可知当a斑点的半径大约超过0.05单位时霍尔姆电阻1/（2α）即开始大于a斑点电阻。具有同样电阻的单个接触斑点半径与霍尔姆半径α很接近。格林伍德还计算了a斑点在不同分布时的等效单个接触斑点（电阻相等）半径及霍尔姆半径，如图4-111所示。在每种情况下由霍尔姆半径确定的圆形面积都很好地代表了电接触面积。在许多实际情况下，接触面是没有绝缘膜的，电接触相当均匀地分布在整个视在接触面积中，在这种情况下a斑点的数量和分布对于接触电阻的影响并不大。这个结论又被Nakamura和Mi-nowa等研究者进一步证实，他们用有限元法和蒙特卡洛法来分析a斑点的分布对收缩电阻的影响。他们发现当电接触面积一定时，a斑点在整个视在接触面积中的位置对收缩电阻没有影响。仅当a斑点被局限在视在接触面的边缘部位时才对收缩电阻有较大影响。即使是在这种情况下的收缩电阻也只是所有a斑点都集中到视在接触面中心位置情况的2倍。从上述结果可知，在工程上知道霍尔姆半径就足以估计接触电阻了。作为一个初步近似，霍尔姆半径可以用实际接触面积A估算为（A/π）^1/2。

表4-12 a斑点半径对收缩电阻1/（2na）和霍尔姆半径α的影响

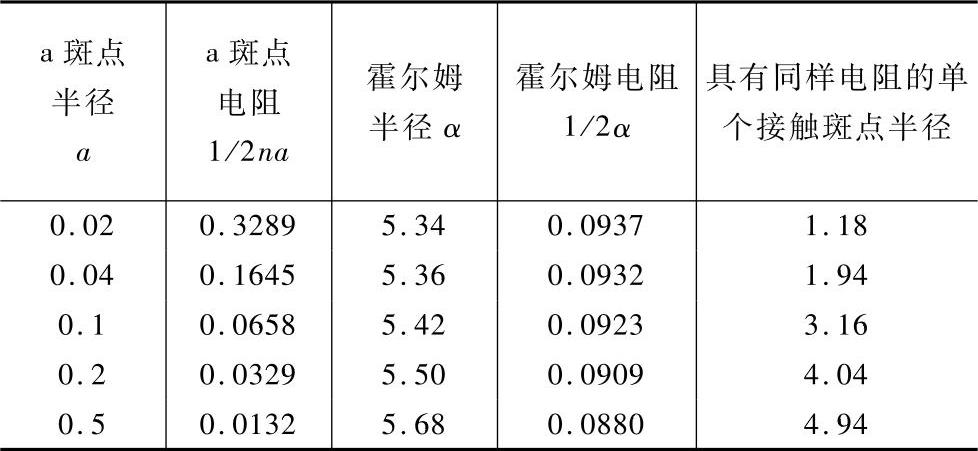
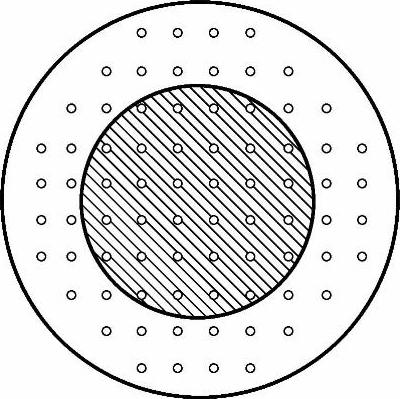
图4-110 a斑点阵列图（阴影区域是与其电阻相等时单个斑点的面积，外面的圆轮廓线半径是斑点群的霍尔姆半径）

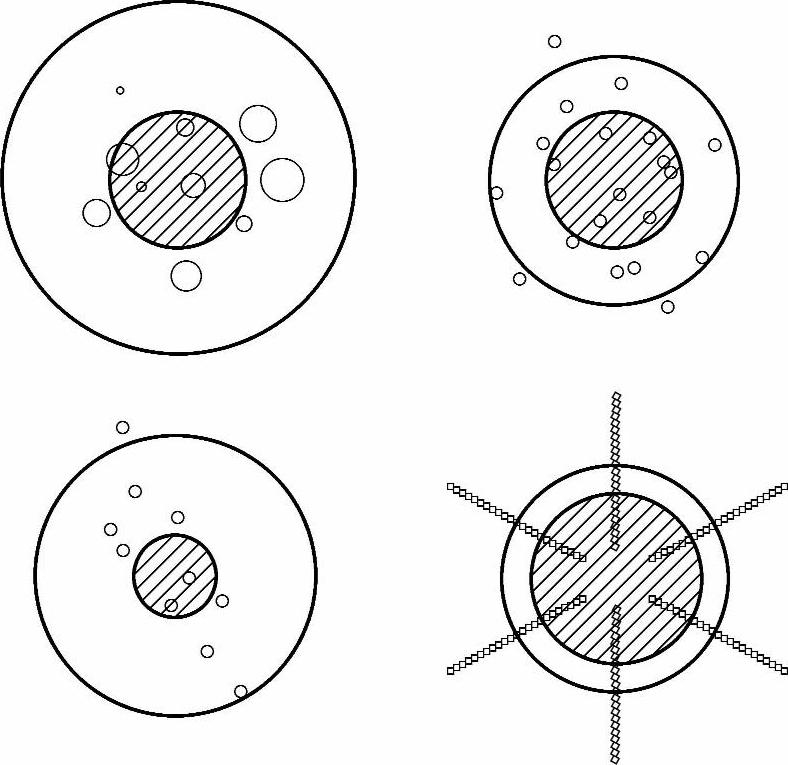
图4-111 不同排列的a斑点群（阴影区域是与其电阻相等的等效单个斑点的面积，外面的圆轮廓线半径是霍尔姆半径）

因为实际接触面积A比视在接触面积小得多，因此a斑点需承受的压力可与材料的强度相比拟。现已广泛认可真实接触面积是由接触头的塑性变形引起的。Greenwood和Wil-liamson证明了在大多数实际情况下表面形貌的变形都是塑性的。Bowden和Tabor提出接触面微观形貌上的接触压力等于相接触的两种材料中较软的一种的蠕变压力，即视在负载是由较软的微突起的塑性流动来承担的。按照这种假设，机械接触面积A_c与施加在接触面上的负载以及相对较软的材料的硬度（塑性蠕变应力）H之间存在如下关系：

F=A_cH （4-91）

表达式（4-91）非常有用，它可以很有效地解释接触电阻测量结果。它表示两个表面之间真正的机械接触面积与视在接触面积无关，即A_c=F/H，它只与接触压力和接触材料的硬度有关，并且它与接触物体的尺寸也无关。这是一个令人吃惊的结论，让我们用这个例子作一个说明，当两个材料相同尺寸不同的导体相接触，一个面积为1cm²，另一个面积为10cm²，两个导体上施加接触压力F。如果两种材料的表面加工情况相同，它们表面微突起的密度应该相同。这样如果小的接触面有n个微突起的话，那么大的接触面则会有10n个微突起，在小接触面上每个微突起的平均机械负载为F/n，而在大接触面上则为F/（10n）。如果微突起的变形是完全塑性的，那么在小接触面上平均每个微突起的接触面积将是大接触面的10倍，而两个面上总接触面积相等。

如果接触面上没有绝缘膜，并且在霍尔姆半径α内分布着足够多的a斑点，那么可以从表4-12的数据中推断接触电阻约为

R_c=ρ/（2α） （4-92）

以及A_c=ηπα²，式中η为一个经验系数，对于清洁的接触面经验值为1。将公式（4-91）引入可得接触电阻为

这个表达式在较大的机械负载范围内具有广泛的有效性，对于多种触头材料它的结果与发表的实验结果相一致，如图4-112～图4-114所示。如果接触面上有绝缘膜存在，那么在式（4-93）的右端项上要增加一项。

公式（4-93）的简单性加上其在很广的范围与实验结果的一致性掩盖了电接触中物理现象的复杂性。图4-112～图4-114所示的接触电阻随负载的增加而减小，这是在几个因素的共同作用下出现的，其中最重要的如下：

1）随着负载的增加表面相接触的微突起数量也增加；

2）相接触的微突起塑性变形被压成平面，这减小了每个a斑点的收缩电阻从而也减小了总接触电阻；

3）微突起的变形引起的加工硬化。

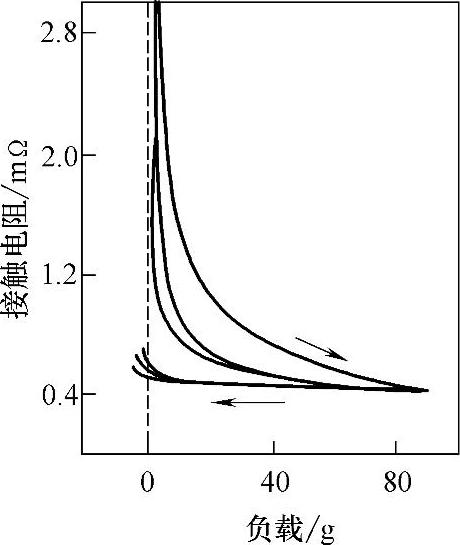
图4-112 表面清洁的纯金表面在空气中接触时接触电阻与负载的关系（箭头指向为施加负载的方向）

最后一种效应使得已接触的微突起趋于平坦的趋势减缓，从而也降低了在负载增加时新的微突起参与接触的速率。在图4-112和图4-113中我们观察到在负载减小时接触电阻增加得相对缓慢，这是由于微突起的塑性变形使接触处成为平面接触造成的，图4-113中曲线1为式（4-93）计算得到的结果，曲线2和曲线3为实验结果（×表示负载增加时第一次测试结果，Δ表示负载减少加时第一次测试结果）。

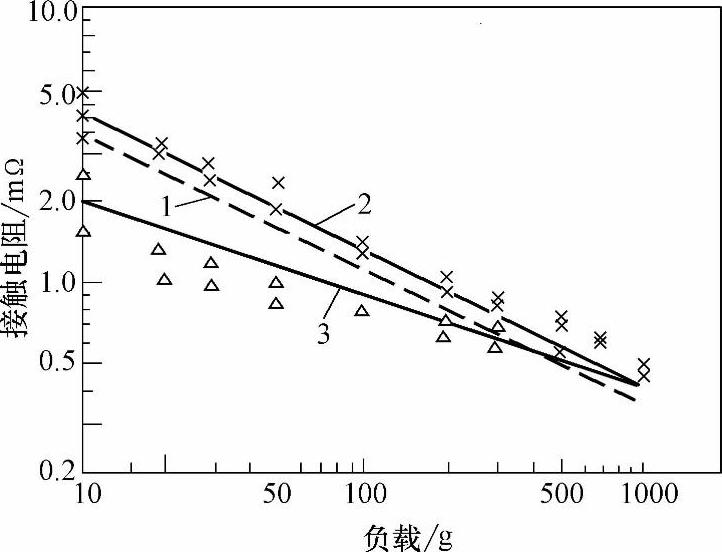
图4-113 接触电阻与负载的关系，触头材料为Ag90Pd10

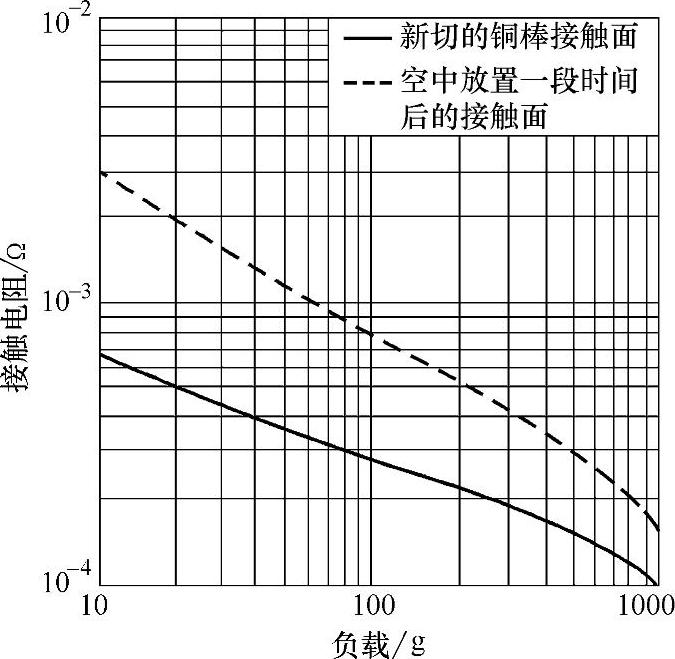
图4-114 刚切出来的铜棒相互交叉接触（实线）与同一对铜棒在空气中放置很长时间交叉接触（虚线）情况下接触电阻与负载的关系

对图4-112～图4-114的特性用数学模型进行分析后的结果显示接触电阻与机械负载的关系与式（4-93）差别不大。这说明微突起的塑性变形过程并不重要，同时也说明式（4-93）推导过程的假设并没有过于简化。式（4-93）现在广泛地被设计工程师所接受，在材料硬度和接触负载已知的条件下来估计收缩电阻的值，得到的结果与实际测量值误差在20%以内。