间隙中气体的击穿现象与特点

让我们来看一看图4-4，它示出了一个电子与触头间隙中的气体分子或原子间可能发生的相互作用。触头上施加恒定电压U，触头间距离为d，触头间气体为空气，气压为一个大气压。单位长度上的电压，即U/d，称为电场强度。如果一个电子出现在触头间的气体中，由于它带负电，因此它开始向阳极移动并获得能量，直到它与一个气体分子或气体原子发生碰撞为止。一个电子在1V电压作用下所获得的动能是1eV（1.6×10^-19J）。在两次碰撞之间电子获得的最大动能为

式中 λ——电子在两次碰撞之间所走的平均距离，叫做平均自由程。

在图4-4中，电子在气体中两次碰撞之间所获得的平均能量是3eV（Eλ=3×10⁶×10^-6eV）。电子与气体分子的碰撞有两种方式。

第一种是弹性碰撞：此时电子与气体分子的碰撞就像一个小玻璃球与一个大保龄球的碰撞相似。碰撞后动量守恒，而且由于电子的质量m_e远远小于气体分子的质量，所以电子能量的损失接近于零。在碰撞之后，电子继续从电场中获取能量。

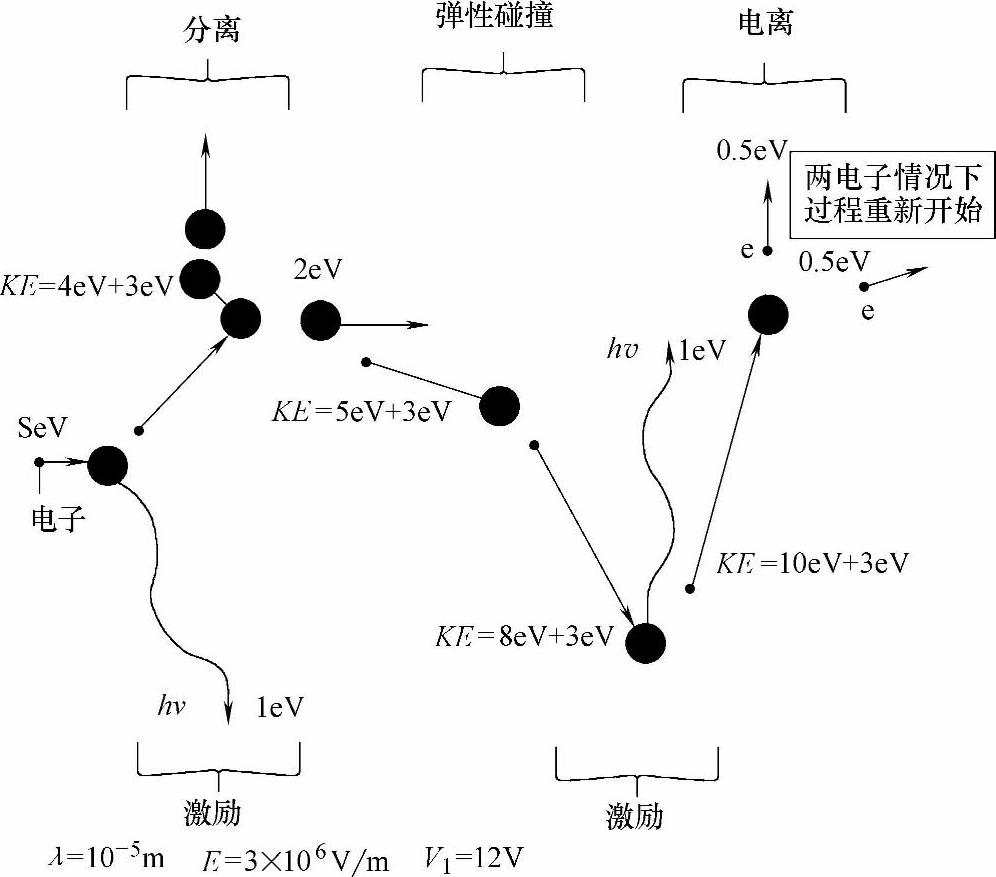
图4-4 电场加速下的电子与气体分子间可能发生的相互作用

第二种是非弹性碰撞：此时电子把它的一部分能量转移给气体分子或原子。正是这些非弹性碰撞才最终导致电弧的出现。非弹性碰撞有多种类型，下面简要地介绍三种类型：

1）解离：解离是将分子分开变成原子的过程。例如一个氮分子可以解离成两个氮原子。当电子的能量大于分子结合能时解离就可能发生。

e+N₂→e+N+N （4-10）

2）激励和跃迁返回：在经过激励和跃迁返回过程后，气体发光。图4-5所示为激励和跃迁返回的过程。由于电子的碰撞，原子中的一个电子跃迁到一个更高的能级，此时原子处于激发态。处于激发态的原子一般很不稳定，被激发的电子在小于1ns的时间内又重新回到原来的能级。不同能级间的能量差以光子的形式放出。

e+N→N^*+e （4-11）

然后

N^*→N+hv （4-12）

式中 h——普朗克常数；

v——光频率。

3）电离：电离过程可直接导致电弧的出现。如果碰撞电子的能量大于或等于使原子中约束最弱的电子释放的能量，那么碰撞电子就有机会使这个约束最弱的电子成为自由电子，如图4-6所示。这个过程的结果是出现一个正离子及两个电子，即初始碰撞电子和从原子中释放出的自由电子。

e+N→2e+N⁺ （4-13）

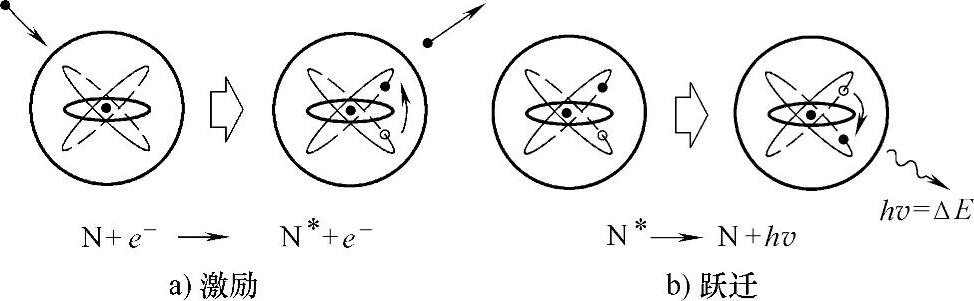
图4-5 激励和跃迁返回产生发光的过程

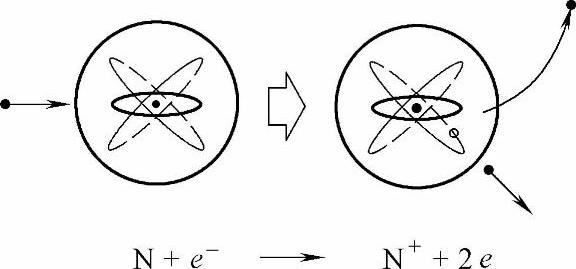
图4-6 电离过程释放出一个电子留下一个正离子

使原子中约束最弱的电子释放的最小能量叫做“电离能”。开关电弧中常见原子的电离电位V_i列于表4-1中。电子的碰撞能量取决于电场强度E和它在相邻碰撞之间的加速距离。若电子的平均自由程为λ，则在1m长度内一个电子的平均碰撞次数为1/λ。一些气体的平均自由程λ由表4-2给出。如能算出碰撞引起电离的概率，即可求得碰撞电离系数α：电子在电场方向运动时每米与气体原子发生的电离碰撞次数。

表4-1 电离电位值

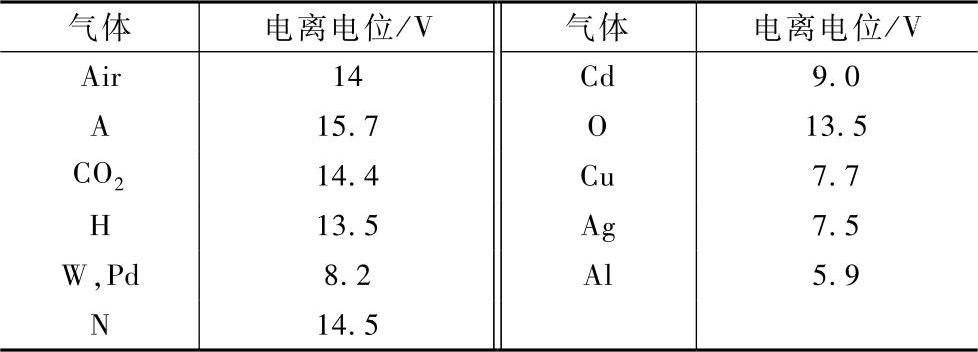
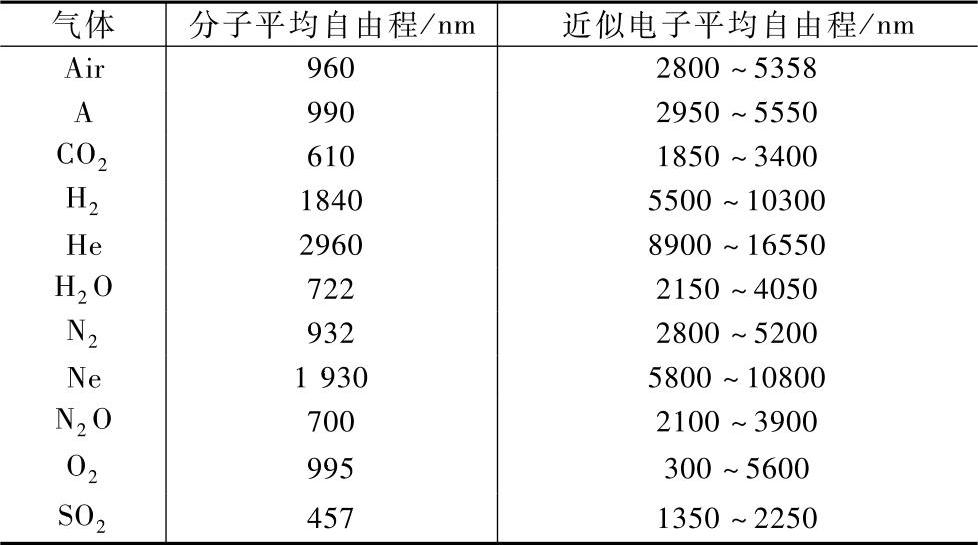
表4-2 在大气压和室温下分子和电子的平均自由程

设在x=0处有n₀个电子沿电力线方向运动，行经距离x时还剩下n个电子未发生过碰撞，则在x到x+dx这一距离中发生碰撞的电子数dn应为

式中负号是考虑增量dn实际上是负的，将上式x从0到x，n从n₀到n积分得

电子如产生碰撞电离，必须满足原子或分子获得的能量大于或等于其电离能这一条件

式中 W_i——电离能；

V_i——电离电位。

令相应的x为x_i，代入式（4-15）中得

对于一个电子来说，exp（-x_i/λ）表示电子沿电力线方向运动x_i距离而未发生碰撞的概率，也就是电子有条件积累足够的能量达到电离能的概率。

电子在电力线方向运动1m的碰撞次数为1/λ，其中有exp（-x_i/λ）的概率产生碰撞电离，则碰撞电离系数α为

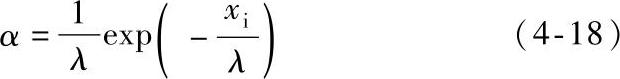
将式（4-16）代入得

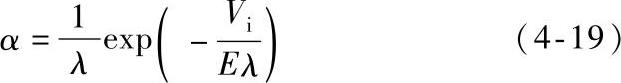
电子的平均自由程与气体的性质（气体分子的大小）和密度有关。对于同一种气体，平均自由程与气体密度成反比，即与温度T成正比而与气压p成反比

因此当气温恒定时

式中 p——气体压力；

A——与气体性质有关的常数。(www.xing528.com)

将式（4-21）代入式（4-19）得

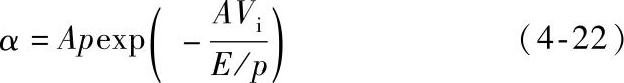
α又称为汤逊第一系数。

如果两个触头分开的距离为d，阴极表面初始电子数为n₀个，当初始电子到达距阴极表面x距离时电子数已增加到n个。这n个电子再行进dx后又产生dn个新电子，即

dn=nαdx （4-23）

将式（4-23）x从0到x，n从n₀到n积分，并考虑均匀电场中α不随x而变化，得

n=n₀exp（αx） （4-24）

因此最终到达阳极的电子个数n₁为

n₁=n₀exp（αd） （4-25）

如果把它换算成电流为

I=I₀exp（αd） （4-26）

然而如图4-7所示，如果I/I₀超过一定值后，电流I的增长就会超过由式（4-26）所给出的值。其原因是随着电离过程电流在不断增加，因此离子的数目也在不断增长，向阴极运动。当这些离子到达阴极后，它们轰击阴极使其释放出更多的电子。释放出的电子会引发二次电离过程，使得电流的增加比式（4-26）中给出的快。此外还有其它的二次电离过程会使阴极释放出更多的电子，如光电发射，它同时还增加了气体中的电离过程。

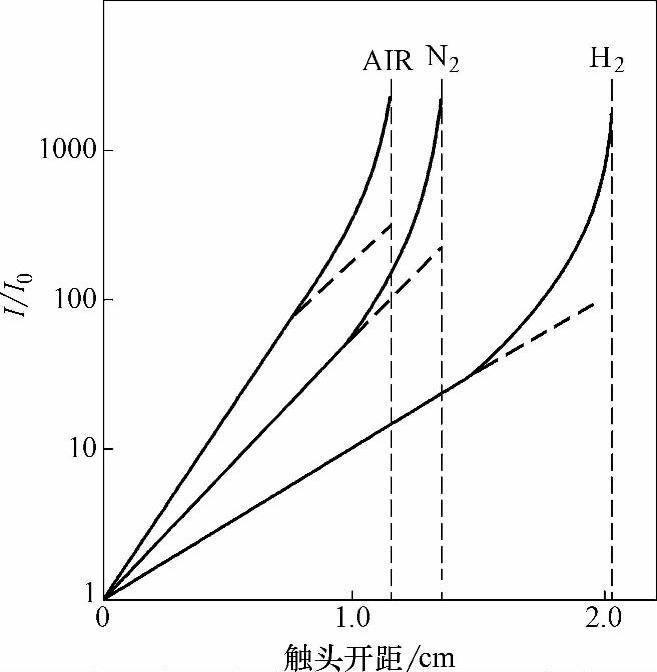
图4-7 在空气、氮气和氢气中汤逊击穿过程的log（I/I₀）与触头开距关系曲线

如果假设由于离子的轰击使阴极发射出更多的电子，让我们用一个参数γ（称作汤逊二次系数）来表示平均每个正离子轰击阴极所发射出新电子。另外，还假设每秒到达阳极的电子为n₁/m²，每秒离开阴极的初始电子为n₀/m²，在所有的效应作用下总和起来每秒由阴极发射的电子为n_c/m²，则气体中碰撞产生的正离子数应为n₁-n_c个。这样由阴极发射的总电子数为初始电子数与离子轰击阴极发射出新电子数之和

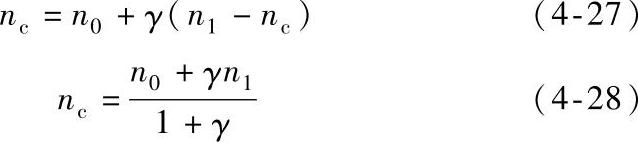
由式（4-25），到达阳极的电子个数为

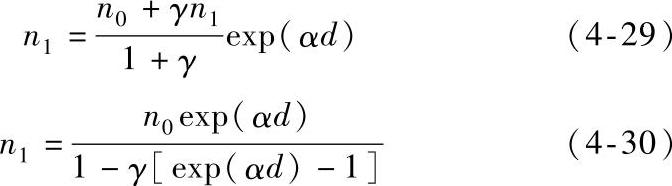
换算成电流为

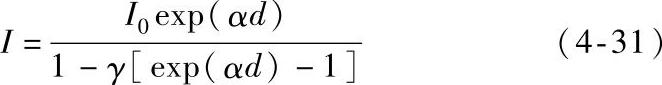
由于exp（αd）1，有

当触头间隙的电场不断增加时，电流随之增加，放电从一种非自持暗放电状态突然转变为某种自持放电状态。如果放电是基于两个汤逊系数所描述的机制引起的，则叫做汤逊击穿。其放电状态的转变以火花放电的形式表现出来，此时间隙中的电流迅速增加，同时伴随着触头间突然出现的亮光。电弧就是由这个火花放电所引起的。

由式（4-32）可知，当γexp（αd）→1时I→∞。因此均匀电场中自持放电的条件为

当距离为d的间隙击穿时

E=U_B/d （4-34）

式中 U_B——击穿电压或火花放电电压。

由式（4-22）可知

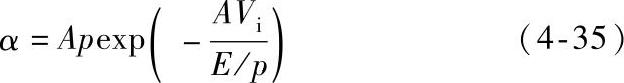
由式（4-34）、式（4-35）可得

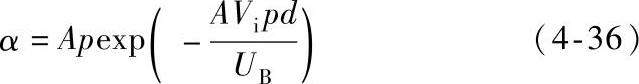
将式（4-36）代入式（4-33）中，得

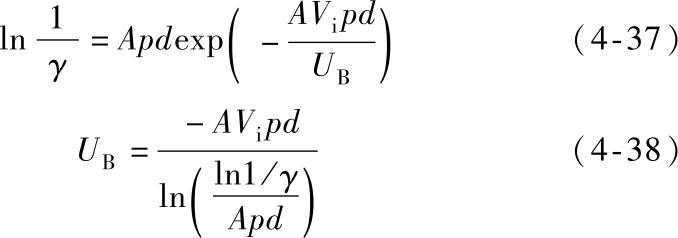
由此可知，对于给定的某种气体，其电离电位V_i为某一确定值，此时击穿电压U_B就只是气体压力与触头间隙距离乘积（pd）的函数。这种关系称为巴申定律（Paschen’s law），是巴申于1889年发现的。由式（4-5）p=nkT，又得到

U_B=f（nd） （4-39）

图4-8所示为空气的巴申曲线。在触头开距一定时，在较高的气体压力下，即曲线最低点的右侧部分，电子平均自由程很短，电子在频繁地碰撞中损失很多能量，为了达到击穿条件电场必须很强使电子在相邻的碰撞中可获得足够的能量，由于E=U_B/d，因此击穿U_B增加；在气体压力较低时，即曲线最低点的左侧部分，电子在碰撞到一个原子之前可以走了较远的距离，但同时发生碰撞的概率大大减少，要达到击穿条件必须使每次碰撞的电离概率增加，为了具有更大的电离概率，电子必须从电场中获得更多的能量，因此击穿U_B也会增加。表4-3给出了某些气体的最小击穿电压（U_B）_min和最小（pd）_min值。注意对于一个给定的U_B有两个pd值。因此对于一个给定的U_B和气体压力下有两个可能出现击穿的间隙距离。由此可以看出，为了避免发生击穿，人们的第一反应就是增加触头开距，这种方法并不一定是适用的。

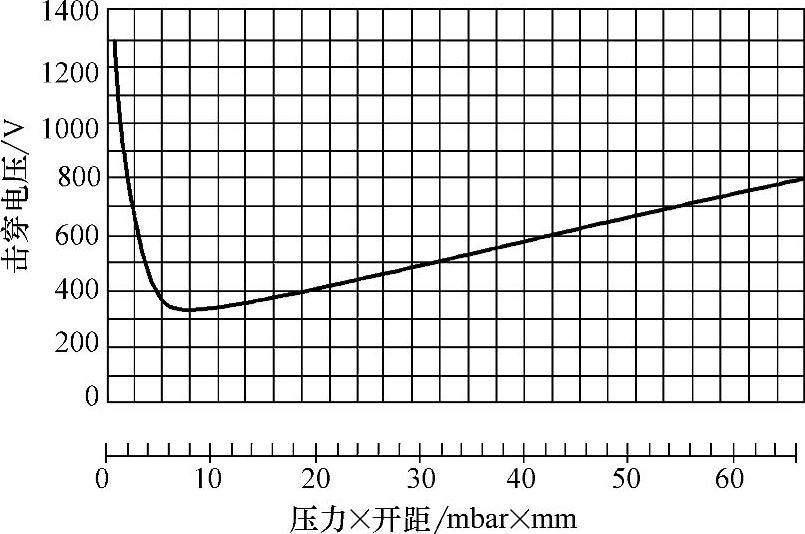
图4-8 空气的巴申曲线

注：1mbar=100Pa。

表4-3 某些气体的最低击穿电压（U_B）_min和最小（pd）_min值

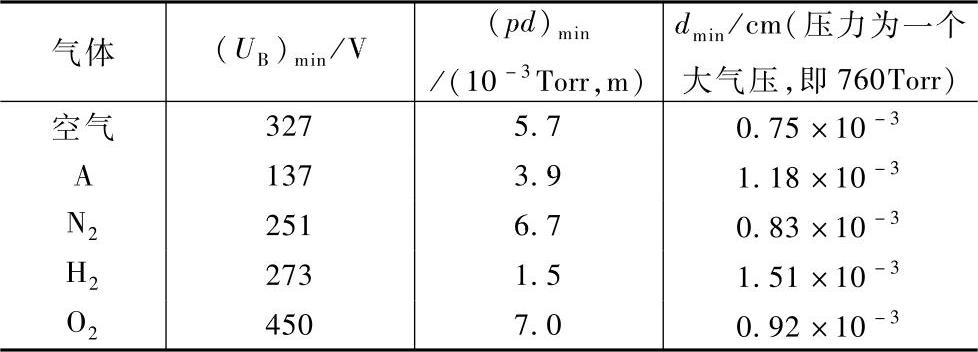
注：1Torr=133.322Pa，后同。

在电器开关领域，初始电子来自于阴极的场致发射或其它随机的物理过程。当触头间隙上施加的电压超过击穿电压U_B时，可能要等好一段时间才发生击穿，但是一旦发生击穿，其速度非常快，如图4-9所示。

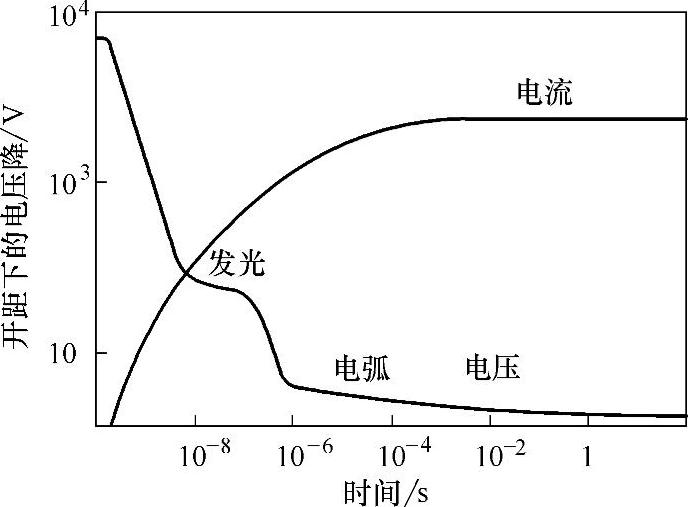
图4-9 触头间隙击穿以及电弧形成的时间