电弧开断：电流开断中的基本要素

电弧的物理基础：自从电流开始流动的那一时刻起，在注意到电流引起的热效应、机械力效应和化学效应之前，人们就知道需要有一种装置可以使得电流的流动开始或终止。

从根本上说，有两种方法可以使电流的流动终止：一种方法是使电路的电源电压为零；另一种方法是使一对触头分开，使载流导体的某一部分形成一个断开间隙。从历史发展来看，第二种方法成为电路开断的最主要方法。

根据历史记录，最早的断路器是水银（汞）开关，它将一对导体棒浸入到装满汞的槽中。后来，随着电流开断技术的发展，水银开关被刀开关所取代，刀开关至今还广泛应用在低压小功率的场合。现在，在最先进的电流开断技术中，电流开断仍然是从一对触头的分开开始的，触头间隙中形成的等离子体连接在两个电极之间。当采用某种技术使得等离子体的电导率大大降低后，其导电性能丧失，从而完成从电的良导体到电的绝缘体的转换，电路开断完成。

在开关中的等离子体称为电弧等离子体，简称“电弧”。电弧是电流开断过程中的一个基本的、不可或缺的，又极为活跃的要素。电弧电导率变化的过程是电流开断的基础。因此对电弧理论的认识和掌握有助于理解电流开断过程。

事实上，利用等离子体实现从电的良导体到电的绝缘体转换这种开关作用是效率最高、成本最低的方法。正如开关电弧研究的先驱者美国西屋电气公司的科学家Joseph Slepian博士曾说，如果大自然没有赐予人类电弧，那我们就一定要把电弧发明出来，否则人们就不得不使用其它更昂贵、更复杂的设备来开断大功率的电路。希望通过本章的介绍，读者可以建立对电弧等离子体的一些认识，为进一步了解电流开断做好准备。

中国古代认为世界由“金、木、水、火、土”五行组成。古希腊认为世界由“土、水、气、火”组成。在现代人们知道宇宙是由“固体、液体、气体和等离子体”所组成的。物质的前三种状态在宇宙中只能极偶尔地在一些像地球这样的冷行星和流星上见到。而第四种状态——等离子体态却是在宇宙中占主导位置的物质状态。例如恒星、星云、星系空间气体、太阳风和地球大气上层全都是等离子体状态。但是物质的前三种状态毕竟是我们日常生活中所熟悉的，因此它们可以作为我们了解物质状态的一些基本概念的起点。

通过加热的方式，物质四种状态之间可以产生转变，我们以水为例进行说明。在一个大气压下，温度低至摄氏零度以下，水凝结成冰，此时物质的微观基本组元——分子的热运动动能小于组元之间的相互作用势能，因而相互束缚，在空间的相对位置固定，这就是固体状态。当体系的温度升高至零度以上，冰融化成水，分子间的热运动能量已经与分子之间的相互作用势能相当。在体系的内部，分子基本上可以自由地移动，但在边界面上，由于存在附加的表面束缚能，大多数分子还不具备可以克服这种表面束缚能的动能，因而存在一个明显的表面，这就是液体状态。当体系的温度高至100℃以上，水开始汽化为蒸汽，分子间的热运动动能足以克服分子间的相互作用势垒，包括表面的束缚能，分子因此变成彼此自由的个体，它们将占据最大可能占据的空间，这就是气体状态。气体分子会与器壁发生强烈地碰撞，气体分子间也会强烈地碰撞。

气体分子或者原子是自由运动的，它们之间以及与器壁之间频繁地碰撞。这些碰撞是弹性的，能量和动量都守恒，碰撞后向各个方向上运动的概率是均等的。碰撞使得能量在分子间及原子间不停地交换，由统计力学可得到此能量的稳态分布。气体的总动能和每个原子的平均动能取决于绝对温度T。动能在每个自由度上是相等的，为kT/2，其中k为玻尔兹曼常数（1.38×10^-23J/K）。这样对一种有三个自由度的单原子气体有

式中 m——气体原子质量；

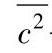——速度二次方的平均值。

这样每m³单原子气体的总动能为

式中 n——每m³的气体原子数量。

对于双原子分子如N₂，它又多了两个自由度，回旋转自由度和振动自由度，总动能是5nkT/2。由式（4-1）中可知速度二次方平均值等于3kT/m。平均速度与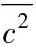的二次方根值相近，但是它们并不相同。平均速度c定义如下：

当采用平均速度c时，我们实际上假定了一些原子运动比平均速度慢，另一些则比平均速度快。考虑到碰撞过程的随机性，麦克斯韦（Maxwell）和玻尔兹曼（Boltzmann）指出，在总数为n的原子中，速度在c和c+dc之间的原子数dn由下式决定：

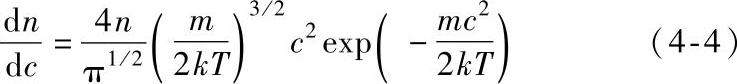
图4-1所示为麦克斯韦-玻尔兹曼分布函数。从图中可以看出一些原子运动比平均速度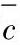快得多，另一些则比平均速度慢得多。在任何给定的时间内，有近90%的原子速度在到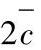之间。其中可能性最大的速度是c₀=（2kT/m）^1/2。气体的压力由下式决定：

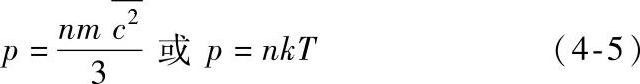(www.xing528.com)

如果气体是由分子组成的，当继续加热时，分子的平均动能就会大于分子的结合能，分子会解离成原子。当温度进一步增高，原子间的热运动动能与电离能相当的时候，原子就会被电离，即原子开始失去电子。如果失去一个电子，原来的中性原子就带有一个正电荷。失去电子的原子叫做正离子，正离子简称离子。离子和电子一起组成了物质的第四态——等离子体态。

图4-1 N₂在三种温度下的麦克斯韦-玻尔兹曼速度分布

等离子体可定义为，由大量带电粒子组成的非束缚态宏观体系。其特征是正电荷和负电荷在时间和空间上的平均密度都近似相等。电荷密度相等，即准电中性是等离子体非常重要的性质。在开关中，等离子体就是在触头间“燃烧”的电离气体，即电弧。

电弧这个术语最早是由戴维（Sir Humphrey Davy）在19世纪早期引入的。他在观察两个平行导体间的放电时，发现处于中间发热发光的部分由于对流作用向上运动，而弧根部分保持不动，从而得名电弧。等离子体这个术语最早是由朗缪尔（I.Langmuir）在19世纪末给电弧中的物质起名字时提出的。对于电弧和等离子体直到1897年汤姆逊（Thomp-son）发现了电子和1901年玻尔（Bohr）建立起原子模型后才开始得到定性的理解。1915年汤逊（Townsend）发表了一部经典著作《气体中的导电性》（Electricity in Gases），从此为等离子体领域打下了坚实的基础。

假设我们把N₂加热到20000K，先暂且不论是如何做到的，由图4-2可以看到当温度增加时氮分子会发生怎样的变化。在大约4000K时N₂分子开始解离成单个的N原子。在约5000K时N原子开始电离形成等离子体。在约20000K时几乎没有中性气体存在，全部形成了等离子体（完全电离）。当温度再升高N原子逐渐失去两个电子变成2价正离子。如果想把N原子的所有电子全部拉出则需要数百万度的高温。对于开关装置中触头之间的电弧来说，其温度大约在6000～20000K之间，主要取决于电流大小及开关的设计参数。

让我们对电弧的温度做一个如下的分析。从式（4-1）中我们知道气体的动能与它的绝对温度T有关。对于一个N离子（m=2.3×10^-26kg），当它的温度达到20000K时其速度的方均根为

这个速度看起来非常高，但是在实验室中却不难做到。拿图4-3中的玻璃真空管作个比方，将其中的气体抽出，在电极间施加电势差U，把一个氮离子放在阳极上，计算一下这个离子达到阴极时速度为4.9×10³m/s所需的U是多少。离子到达阴极时的动能等于其在阳极时的位能，因此

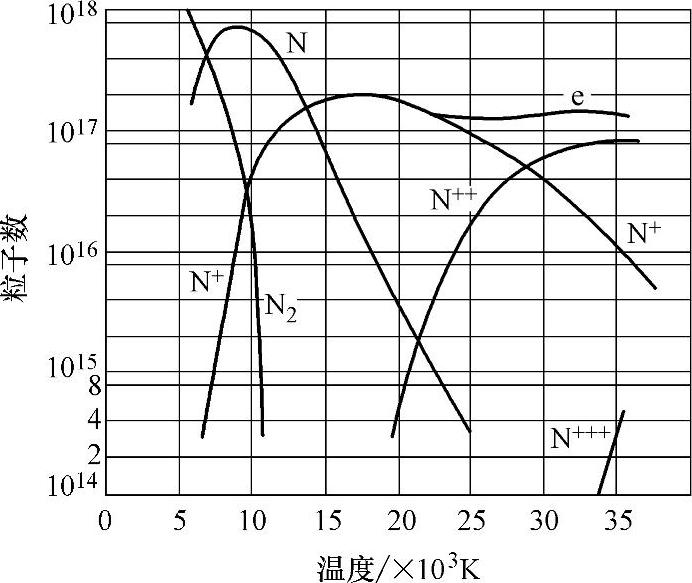
图4-2 大气压下每cm³中N粒子数与温度的关系

电子和一价正离子的电量是1.6×10^-19C。这样对氮离子有

因此得到

U=1.7V （4-8）

由此可知在电极间只要施加一个很低的电压就能把离子加速到一个很高的速度，这个速度对应的粒子温度很高。当然只有当玻璃真空管内是高真空，氮离子无法与其它气体分子相碰撞时才能得到这样的结果。一旦在玻璃管内加入一些氮气，离子与气体分子发生弹性碰撞，离子速度会快速降低到与背景气体相平衡的水平。在低压开关中的电弧多为大气压下的空气电弧。触头间的气体是如何被电离，电弧又是如何形成的呢？这个解答需要从电子与气体分子的相互作用来入手。

图4-3 在真空中加速一个N离子