样本大小的确定方法及注意事项

1.样本n的确定

为使由样本得到的产品总体质量平均值的估计值能满意地反映总体的真实情况，需从总体求取适量的抽样单位（即最小包装件）。抽样单位数（即样本）可由下式求得

n=（Aσ₀/E）²

式中 n——抽样单位数，即样本大小；

σ₀——产品总体质量的标准差估计值；

E——由样本得到的产品总体质量平均值的估计值与用相同方法对每个抽样单位

测量得到的产品总体质量平均值之间存在的最大允许误差；

A——概率系数，它表示从样本得到的产品总体质量平均值的估计值与对每个抽

样单位测量得到的产品总体质量平均值之间存在的误差超过最大允许误差

E的相应的概率。

由下式进行计算，有时使用起来更为方便：

n=（AV₀/e）²

式中 n——抽样单位数，即样本大小；

V₀——σ₀/X，产品总体质量的变差系数估计值，其中X为产品总体质量平均值；

e——E/X，用X的百分数表示的最大允许误差。

2.σ₀或V₀的求取

根据同种产品的历史数据，分别用下式计算出样本大小相等或相近的几批产品的样本标准差或变差系数：

式中 s——批的样本的标准差；(www.xing528.com)

x_i——单个测定值；

x——单个测定值的算术平均数；

n′——批的样本大小；

V′——批的变差系数。

然后，再算出它们的平均值。

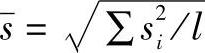或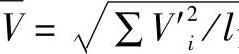分别作为σ₀或V₀的估计值，其中l为批数。

注：在求取σ₀或V₀时，一般来说，样本大小n′越大，批数l越大，则所得结果越准确，但在实际应用时，若n′越大，则批数l可小些，若n′越小，则批数l要大些。如n′大于20时，l取4～5即可；n′为10左右时，则l最好大于10。

3.最大允许误差E或e的确定

最大允许误差E或e可根据“需要”和“可能”进行规定。

所谓“需要”是指对某项质量特性的一点变化就会使产生转型，或对成型加工、制品应用，产生很大影响，则从样本得到的特性估计值的准确度就该高些，即E或e要规定得小些，反之，E或e可规定得大些。

所谓“可能”是指对样本大小，进行测试所需要花费的人力、物力是否合适而言。根据上面的公式可知，样本大小n与最大允许误差的E或e平方成反比。若不必要地把E或e规定得太小，则n将会变得过大，花费的检验费用就很大，这往往是不经济的。因此，如果对某一规定的E或e求出的n太大，则可调整E或e（将E或e增大，即降低估计值的准确度）以求出较小的n。

总之，确定最大允许误差E或e时，所考虑的问题是在所要求的估计值准确度和要得到这样准确度的估计值所花的费用大小之间取得适当的平衡。

4.概率系数A的确定

概率系数可根据对结果所要求的可信区间来定。在工业生产上一般定为1.96就够了，这时从样本得到的产品总体质量平均值的估计值与对每个抽样单位测量得到的产品总体质量平均值之间，存在的误差超过最大允许误差E或e的概率为5%。相应于其他概率的A值，可根据需要，从正态分布表得到。

5.多项质量特性产品样本n的确定

对于塑料树脂产品来说，通常有几项质量特性，则可分别算出各项质量特性所需要的n数，然后取其中最大的2个作为检验批的样本大小，也可用与产品主要用途有关的关键性质量特性中变差系数最大的一个来计算n数。