姿态控制律的设计优化

为了简化控制器的设计任务，根据奇异摄动理论［11］，并结合无人机姿态角和姿态角速度随着外界变化而变化的快慢程度，将无人机姿态控制系统分为慢、快两组动态回路，其中选取姿态角Ω＝［ϕ　θ　ψ］T为慢动态回路状态变量，选取姿态角速度ω＝［p　q　r］T为快动态回路状态变量，建立如下无人机仿真非线性方程组：

联立式（15）～式（17）及各参数表达式，可得

其中，Mc＝［lctlmctlnctl］T＝gf，δδ为滚转俯仰和偏航控制力矩，将其映射成控制舵面偏角δ＝［δa，δc，δr，δy，δz］T，δa、δc、δr、δy、δz分别为副翼、水平鸭翼、单垂尾翼、发动机侧向偏角、发动机纵向偏角，gf，δ的具体表达式为

其中，XT为发动机喷口到无人机质心之间的距离，取8.5 m；q—＝ρV2/2为动压；s、b、c－分别为机翼面积、机翼翼展和平均气动弦长；T为发动机的推力。

参照相对阶ρ的定义，联立式（1）、式（16）、式（17），很容易得出本系统慢、快动态回路的相对阶均为ρ—＝1，通过控制阶的选取，对闭环系统稳定性影响因素进行验证，取控制阶r—＝0，代入式（7）～式（11），得

因此，根据式（6）和式（14）得出考虑不确定因素，并基于NG-PC的慢动态回路控制律表达式为

式中，，Ts为慢动态回路的预测时间，取0.4 s；由ϕc、θc、ψc经过一阶惯性微分环节得到；慢动态回路的控制输出作为快动态回路的期望输入。(https://www.xing528.com)

同理，基于NGPC的快动态回路控制律表达式为

式中，，Tf为快动态回路的预测时间，取由pr、qr、rr经过一阶惯性微分环节得到。

接下来，根据式（13）首先构造如下慢动态回路SMDO模型对不确定因素Ds进行估计：

式中，ss＝［ss，1ss，2ss，3］T；vs＝CsSδs，Cs＝diag｛0.15，0.15，0.15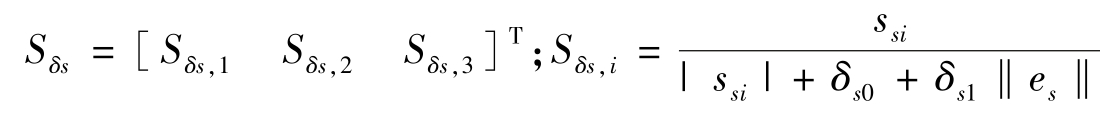｝；，i＝1，2，3；es＝Ω－Ωc；δs0、δs1均为常数，其值分别取0.005和1。

同理，设计快动态回路SMDO模型为

式中，sf＝［sf，1sf，2sf，3］T；vf＝CfSδf，Cf＝diag｛5，5，5｝；Sδf＝，i＝1，2，3；ef＝ω－ωc；δf0、δf1均为常数，其值分别取0.01和1。