滑翔段轨迹设计及控制量求解优化

在超高声速飞行器再入滑翔及末制导过程中，通常滑翔段的初始速度V0、滑翔段转末制导段的速度Vf和高度hf事先给定，设计滑翔段H-V轨迹满足函数关系式

式中，h0为滑翔段初始高度。

由式（6）可知，在V0、Vf、hf确定的前提下，滑翔段的H-V轨迹由滑翔段初始高度h0唯一确定。

对式（6）连续求导可得

在式（7）中，由于当V∈［V0，Vf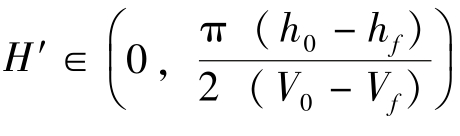］，，因此有H′≥0，且有H′（V0）＝0。

为了使初始下降段与滑翔段光滑交接，且为了设计方便，初始段与滑翔段交接点需要满足一阶导数条件［4］：

式中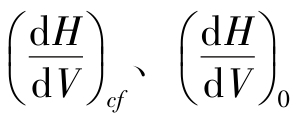，、Vcf、V0分别为初始段末端点与滑翔段初始点上高度对速度一阶导数和该点速度。

由式（7）可以得到H′（V0）＝0且与参数取值无关，因而式（6）所示的H-V轨迹能够直接满足一阶导数条件。

由于攻角方案α（V）已经确定，所以只需求解侧倾角指令σ，即可确定滑翔段轨迹。H对V求导并考虑式（1）中的第1、4式可得

式（7）与式（10）相等即，然后可确定θ（V）。同理，H对V求二阶导数并考虑式（1）、式（10），有

其中，

式（8）与式（11）相等，即，则可求得，考虑式（1）中第2式，将其代入，即可求得cosσ为

对式（14）进行反余弦求解即可得到滑翔段侧倾角指令σ［9］。

需要说明的是，如果出现的情况，则无法求解σ，即出现奇异现象，而cosσ的取值与滑翔段轨迹的设计形式有密切的关系。(www.xing528.com)

本文设计的滑翔段H-V方案只取决于初始高度h0，因此，该方法的主要思路为：通过计算，获得H-V轨迹既在再入走廊内又不会出现控制量侧倾角奇异的初始高度集合，即得到滑翔段初始高度h0的可行范围D。

假设在速度由V0减小为Vf的过程中，由h0决定的轨迹高度满足Hmin≤H≤Hmax，即得到的H-V轨迹在再入走廊内，则此h0可行，这些可行的h0组成可行域D1。假设在H0min≤h0≤H0max（H0min、H0max分别为速度为V0时再入走廊高度的最小和最大值）范围内，能够保证控制量求解不出现奇异现象的h0的可行域为D2。

再入走廊确定后，即可确定H0min和H0max，初始速度V0确定后，h0可以从最低点开始以固定步长Δh递增判断是否满足Hmin≤H≤Hmax，进而确定D1。同理，可以通过求解式（14）判断是否奇异，即此时的h0是否可行，进而确定可行域D2。最后取D1、D2交集即可最终确定h0的可行域D，此可行域可作为再入初始段轨迹设计的末端约束，为再入初始段轨迹的设计提供参考信息。若D为空集，即式（6）的H-V轨迹无法取得，原因在于再入走廊设计得不合理。例如，走廊在V＝Vmax时高度范围过高，因此无法求得不出现奇异的侧倾角指令，需要调整再入走廊，途径为调节滑翔段攻角方案，在导弹合理的滑翔攻角范围内重新选取攻角αH，设计再入走廊。

求得滑翔段初始高度h0范围后，初始下降段设计需要考虑末段高度、速度、弹道倾角约束，由于高斯伪谱法在约束处理上具有精度高、速度快的优点，且Matlab GpopsⅡ工具箱相对成熟，使用方便，因此本文初始下降段采用高斯伪谱法求解弹道。由于初始段轨迹设计不是本文的重点，因此省略具体求解过程。

综上，本文基于H-V规划的再入滑翔制导方法的具体步骤为：

步骤一：根据飞行器的总体参数确定再入滑翔段攻角方案与路径约束（热流密度、过载、动压约束、准平衡滑翔约束）。

步骤二：将过程约束进行H-V转化，确定H-V再入走廊上下界。

步骤三：给定滑翔段的初始速度V0、末端速度和高度Vf、Hf，确定如式（6）所示的再入滑翔段H-V轨迹。判断起始高度h0的可行域D1、D2，得到D进入步骤四，否则回到步骤一重新调节攻角方案。

步骤四：将D作为初始段末端高度约束，通过高斯伪谱法等方法设计初始段轨迹，确定满足初始段约束的某个h0。

步骤五：根据h0确定式（6）所对应的滑翔段H-V轨迹，并求解理想侧倾角指令，完成再入滑翔轨迹设计。

将上述步骤绘制成流程图，如图2所示。

图2　基于H-V规划再入滑翔制导方法流程图