粒子群算法优化：理论与实践

1.粒子群算法的由来及其创新思想

粒子群算法，也称粒子群优化算法（particle swarm optimization，PSO），是一种新型的仿生算法，由J.Kennedy和R.C.Eberhart，在1995年IEEE的国际神经网络学术会议上首次提出。Kennedy的思想来源于20世纪90年代建立的人工生命和演化计算理论。众所周知，单个生物如蚁、鸟、鱼、虫等并不是智能的，但这些生物的群体却表现出处理复杂问题的能力。Reynolds对鸟群觅食行为的研究发现，每只鸟仅仅追踪有限数量的邻居，但最终结果是整个鸟群好像在某个中心的控制之下飞行。这一现象说明，复杂的全局行为可以由简单规则的相互作用形成，其表现取决于群体搜索策略和群体信息之间的交换。

1987年，Reynolds提出了一种名为Boids、具有生命行为特征的人工生命系统。该人工生命系统依据三条简单的规则，模拟了自然界中鸟类等群居动物聚类飞行的行为。群体中的每个个体只需依据三条规则调整自己的行动，即可使群体表现出非常复杂的行为模式，其具体规则为如下。

（1）分离：尽力避免与邻近个体发生碰撞。

（2）结盟：尽力与邻近的个体保持相同的速率。

（3）凝聚：尽力朝与其邻近的个体的平均位置移动。

仿真实验结果表明，在这三条简单规则的指引下，Boids系统就能呈现非常逼真的群体聚集行为，鸟类成群地在空中飞行，当遇到障碍时它们会分开绕行而过，随后再重新聚集为群体。这是首次将生命科学中的概念引入计算机科学。不过，Reynolds仅仅将其作为复杂适应系统（CAS）的一个实例进行仿真研究，而未用于优化计算，故没有实用价值。

Kennedy和Eberhart改进了Boids模型。他们根据鸟群的觅食行为，来优化鸟群系统的寻优过程和寻优结果。具体而言，他们用一点来表示食物，所有的鸟根据其他鸟的觅食信息调整自己的行为方式。实验结果发现，该模型在多维空间中具有很强的寻优能力。以此为基础，作者进而采用无质量、无体积的“粒子”（particle）来表示每一个个体，并依据粒子的觅食要求，为每个粒子规定了简单的行为规则，将问题的目标函数度量成个体对环境的适应能力，将生物的优胜劣汰过程类比为可行解变换优化的迭代过程，从而形成一种以“生成+检验”为特征的人工智能算法，即粒子群算法。

从创新的角度看，粒子群算法的主要创新思想有：

（1）分布式算法。类似于Boids群的仿生运动，个体按照既定规则运动，而群体行为则是个体行为的分布式涌现。

（2）两种极值迭代。人们在决策过程中，使用了两类重要的信息，一种是自身的经验，另一种是他人的经验。在粒子群算法中，创立者则提出每个个体根据个体极值和全局极值进行迭代，从而达到整个种群不断接近最优解的目的。

（3）保持稳定性和适应性。粒子群的群体，通过各粒子自身的最佳位置信息和种群的最佳位置来对周围环境的品质因素作出响应，并采用一定方式分配这种反应，从而体现出种群的多样性；只有当粒子群中的最优粒子发生改变时，粒子行为才发生改变，因此保持了粒子群的稳定性和适应性。

（4）惯性权重的设置。早期的粒子算法是没有惯性权重的，被称为原始PSO。为了平衡算法的全局搜索能力和局部搜索能力，创立者提出惯性权重的概念，用以调节算法的继承性和发展性。惯性权重的实质是体现了算法对粒子原有速度继承的多少：在一定范围内的惯性权重越大，则粒子受原速度的影响越大，受当前环境的影响越小，表现为粒子的发散性越强，因此算法的全局搜索能力越好；反之，惯性权重越小，则粒子受原速度的影响越小，受当前环境的影响越大，表现为粒子的收敛性越强，因此算法的局部搜索能力越好。通常将包含惯性权重的粒子群优化算法称为标准粒子群优化算法。

2.标准的粒子群优化算法及其流程

Kennedy和Eberhart最初提出的粒子群优化的算法称为原始粒子群算法。他们将每个粒子视为优化问题的一个可行解，粒子的好坏由一个事先设定的适应度函数来确定。每个粒子将在可行解空间中运动，并由一个速度变量决定其方向和距离。通常粒子将追随当前的最优粒子，并经逐代搜索最后得到最优解。在每一代中，粒子将跟踪两个极值：一个是粒子本身迄今为止找到的最优解，另一个是整个群体迄今为止找到的最优解。

式（9.9.3）是原始粒子群算法的数学模型。式中的c1和c2为学习因子，也称加速常数（acceleration constant），根据经验，通常c1=c2=2。r1和r2为［0，1］范围内的均匀随机数。式（9.9.3）的上式右边由三部分组成，第一部分为“惯性”（inertia）或“动量”（momentum）部分，反映粒子的运动“习惯”（habit），代表粒子有维持自己先前速度的趋势。第二部分为“认知”（cognition）部分，反映粒子对自身历史经验的记忆（memory）或回忆（remembrance），代表粒子有向自身历史最佳位置逼近的趋势。第三部分为“社会”（social）部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体或邻域最佳位置逼近的趋势。

考虑到粒子对原有速度继承性的影响及环境对速度的影响因素，从而在粒子速度更新公式中增加了权重w，如式（9.9.4）所示：

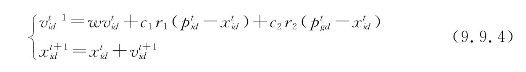
式（9.9.4）称为标准粒子群优化算法的迭代公式。(www.xing528.com)

标准粒子群优化算法的流程图如图9.9.3所示。

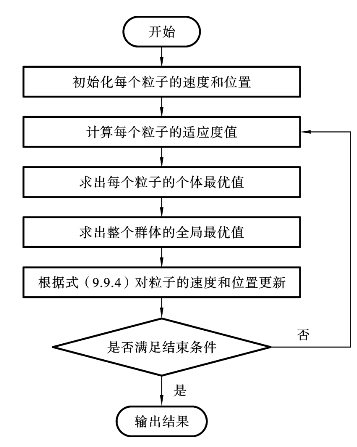
图9.9.3　粒子群优化算法流程图

限于篇幅，上述图中关于初始化的取值，适应度、个体最优值、全局最优值、惯性权值等的选取和计算方法均未介绍，有兴趣的读者请参阅参考文献。

3.粒子群优化算法的特点及其改进

粒子群优化算法本质上是一种随机的搜索算法，并能以较大概率收敛于全局最优解。实践证明，粒子群优化算法适合在动态、多目标优化环境中寻优。粒子群优化算法与传统的优化算法相比具有更快的速度和更好的全局搜索能力，其具体特点如下：

（1）粒子群优化算法是通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索算法。与各种进化算法相比，粒子群优化算法是一种更为高效的并行搜索算法。

（2）PSO与GA有很多共同之处，两种都是随机初始化种群，使用适应度函数值来评价个体的优劣程度和进行一定的随机搜索。但PSO是根据自己的速度来决定搜索，没有GA的交叉和变异。与进化算法相比，PSO保留了种群全局搜索策略，但是因其采用了速度-位移模型，操作简单，避免了复杂的遗传操作。

（3）PSO有良好的机制来有效地平衡搜索过程的多样性和方向性。

（4）在PSO中有每个粒子的最优信息（gbest）可以传递给其他粒子，这是一个单向的信息流动，因此在多数情况下，所有粒子可能更快地收敛于最优解。

（5）PSO特有的记忆使其可以动态地跟踪当前的搜索情况并调整其搜索策略。

（6）PSO在算法结束时，仍然保持个体的极值，而遗传算法在结束时只能得到最后一代个体的信息，前面迭代的信息没有保留，因此将PSO用于调度和决策问题时可以给出多种有意义的选择方案。

（7）PSO在搜索时可以同时采用连续变量和离散变量而不发生冲突，所以PSO可以很自然、很容易地处理混合整数非线性规划问题。

（8）粒子群优化算法对种群大小不是十分敏感，即当种群数目下降时，性能下降不是很大。

粒子群优化算法目前存在的问题如下：

（1）粒子群优化算法理论研究不深入，该算法收敛模型的建立和收敛性分析都很困难。

（2）粒子群优化算法在解决高维或超高维复杂问题时往往会遇到早熟收敛，容易陷入局部极值陷阱。

（3）粒子群优化算法的运行与它所采用的参数取值有较大的关系，因此算法的参数会影响算法的性能和效率。

（4）在收敛的情况下，由于所有粒子都向最优解方向飞去，粒子趋向同一化，失去了多样性，在收敛后期使收敛速度明显变慢，以致算法收敛到一定精度时无法继续优化。

（5）粒子群优化算法存在应用领域的局限。扩大应用领域、改进PSO的拓扑结构、精选PSO的参数和采用混合粒子群算法是发展PSO的重要研究方向。