使用遗传算法优化神经网络的方法

神经网络优化方法的缺点是：要求目标函数连续可微（因为要沿着能量梯度降的方向来修改权值）、训练速度较慢、全局搜索能力弱、易陷入局部极值。遗传算法正好相反，它既不要求目标函数连续，也不要求可微，甚至不要求目标函数有显函数的形式，它仅要求该问题可计算；它的搜索遍及整个解空间，因此容易得到全局最优解；遗传操作比较灵活，只要选择得当，遗传计算的收敛速度会比神经网络计算的收敛速度快。由此可见，用遗传算法来优化神经网络，可以使神经网络具有全局自学习、自组织、自适应和自进化的能力，通常这种优化有下述三种方案。

1.用遗传算法优化神经网络的连接权值

神经网络连接权值包含神经网络系统的全部知识。传统的神经网络方法都是采用某种确定的权值变化规则，通过学习、训练不断调整，最终得到一个较好的权值分布。这种方法的训练时间过长，甚至可能因陷入局部极值而得不到适当的权值分布。如用遗传算法来优化神经网络的连接权值，可望解决这个问题。该法的主要步骤如下。

（1）决定初始种群，把神经网络的节点编号，各节点之间的连接权值Wij形成一个矩阵W=（Wij）N×N，其中N是网络的节点数，Wij=0表示节点i到节点j之间没有连接。

图9.8.1是一个前向神经网络的例子，其中输入层有2个节点，隐含层有3个节点，输出层有2个节点。同一层各节点间无连接，网络无反馈，各节点自身也无反馈。各节点处有阈值θi、θj也形成一个矩阵：θ=（θi）N。对应这一网络的连接权值矩阵及阈值矩阵如下：

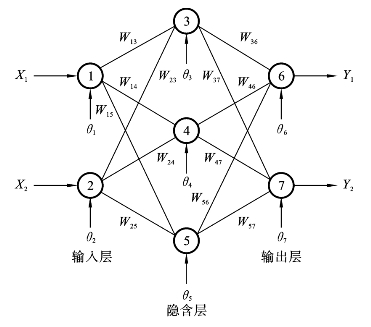
图9.8.1　前向神经网络例子

连接权值矩阵是一个下三角为零的矩阵，这是因为上述神经网络是一个无反馈的前向网络，网络中仅有12个元素，表示了全部网络的连接权值。阈值矩阵是一个7元素矩阵，通常输入层无阈值，即θ1=θ2=0。这样要决定的阈值就是5个，总计连接权值与阈值共有17个。

通常用二进制码串来表示种群中的个体（染色体）。上述12个连接权值和5个阈值组成一组数据，就代表一个个体，若干个这样的数据组便构成初始种群。下面介绍将数据组转换成二进制代码串的方法。

假设所有的权值与阈值在某范围以内，即Wij∈［（Wij）max，（Wij）min］，用l位二进制数来表示上述范围内的权值与阈值，则实际权值（或阈值）与二进制字符串表示的值之间有下列关系：

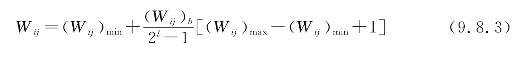
式中：Wij是实际权值；（Wij）b是由l位字符串表示的二进制整数；［（Wij）max，（Wij）min］是各连接权值的变化范围。表9.8.1给出了一个权值范围在-127～+128之间的8位二进制数编码方案。

表9.8.1　8位二进制数编码方案

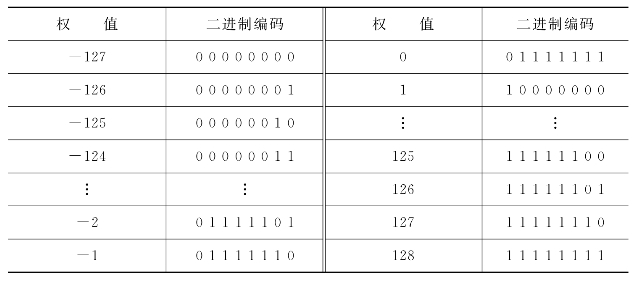
将所有的权值和阈值对应的0/1代码串联在一起，就得到一个初始种群的个体。随机地选取若干个这样的个体，便得到全体初始种群。也可以用十进制数来编码，但遗传操作要在两组实数上进行，原有的二进制代码的遗传操作算子不能直接使用，要为实数的遗传操作单独设计运算规则。

（2）计算适应度。计算适应度的方法有多种，基本上都是以神经网络的输出节点的误差e或相应的网络能量函数E为基础，下列四种方案可供选择。

式中：C为一常数；

e为误差，计算式为

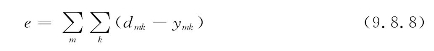
E为网络的能量函数，计算式为

(www.xing528.com)

dmk及ymk分别为第m个训练样本的第k个输出节点的期望输出与实际输出。

由式（9.8.4）～式（9.8.7）可以看出，误差越大，则适应度越小。

（3）选择（复制）操作选择若干适应度函数值最大的个体，直接复制遗传给下一代。

（4）交换及变异操作，对当前一代群体进行交换及变异操作，产生下一代群体。

（5）重复步骤（2）、（3）、（4），使初始权值及阈值分布不断修正进化，直到训练目标得到满足为止。

把遗传算法用于决定神经网络的连接权时，还可以把遗传进化法与神经网络的基于梯度下降的反向传播训练方法结合起来，形成一种神经网络的混合训练方法。这种训练方法可以取两种方法的各自特点。遗传算法有利于全局搜索，而BP算法则有利于局部搜索，所以首先用遗传算法对初始权值分布进行优化，在解空间定位出一个较好的搜索空间，然后用BP算法，在这个较小的解空间中搜索出最优解。一般而言，混合训练的效率和效果比单独用遗传算法或单独用BP算法的效率和效果要好。

2.用遗传算法优化神经网络的结构

神经网络的结构包括网络拓扑结构和传递函数两部分。网络拓扑结构即网络的层次、节点及节点间的连接方式。网络拓扑结构的优劣对网络处理问题的能力有很大的影响。一个好的结构应能圆满解决问题，同时又无冗余点和冗余连接。遗憾的是，至今对神经网络的结构设计仍无系统的方法，还停留在依靠人为经验的阶段。人们只好采用试验或探测的方法来选择较好的神经网络结构。至于传递函数，通常多采用S型函数或双曲正切函数。一般讲神经网络的结构即指其拓扑结构。

用遗传算法优选神经网络的结构的步骤如下。

（1）随机产生N个结构，对每个结构进行编码。编码的方法可以采用上述连接权矩阵的结构编码方法。若节点间无连接，则连接权值为0，若节点数和层数不同，则编码的矩阵大小不同，编码串的长度不同。每个编码串对应一个结构，这就是种群中的个体。

（2）用不同的初始权值分布对种群中的各个结构进行训练（此时采用相同的样本）。

（3）根据训练的结果或其他策略确定每个个体的适应度（例如可以用式（9.8.4）～式（9.8.7）中的某一公式来计算适应度）。

（4）选择若干适应度最大的个体，直接遗传给下一代。

（5）对当前一代群体进行交换和变异等遗传操作，以产生下一代群体。

（6）重复步骤（2）～（5）步，直到当前一代种群中的某个个体（对应着一个网络结构）能满足要求为止。

3.用遗传算法优化神经网络的学习规则

学习规则在神经网络系统中决定了系统的功能。同一个网络，学习规则不同，其效率与效果大不相同。在神经网络一章中，我们介绍过几种学习规则；对于在BP网络中应用较多的广义δ规则，我们还介绍过不同的改进算法。在这里，我们采用遗传算法来设计神经网络的学习规则，其步骤如下。

（1）选择不同的学习规则，每一个学习规则为一个个体，不同的学习规则常体现在学习参数上，所以对学习规则进行编码就是对学习参数进行编码。

（2）给定一个神经网络和一个训练集（输入、输出集），用不同的学习规则进行训练。

（3）计算每个学习规则的适应度（可以用式（9.8.4）～式（9.8.7）中的某一公式来计算适应度）。

（4）根据适应度进行选择。

（5）对每个被编码的学习规则（个体）进行遗传操作，产生下一代群体。

（6）重复步骤（2）～（5），直到达到目的为止。

目前，用遗传算法来改进神经网络学习规则的研究还不多，这是一个非常有前途的研究领域。