调度问题的遗传算法优化解法

1.调度问题的Gantt图表示

表9.7.1给出了一个4作业3设备的车间作业调度问题的例子。对不同的作业（i）预先给定了不同的技术顺序（j）、相应的各操作所用的设备（k）及操作的时间（tijk），所以三元组（i，j，k）及对应的操作时间（tijk）就代表了所给定的调度问题的前提。

表9.7.1　JSSP例子

为了表示JSSP的解，通常应用Gantt图，如图9.7.1所示。图中列出各设备上处理不同作业的技术顺序及相应的操作时间。每个三元组（i，j，k）用一个方框表示，它表示第i作业第j操作在第k设备上执行，方框的长度表示操作（i，j，k）的处理时间tijk，在图9.7.1所示的方框中，填入三元组（i，j，k）。有时为了简化，可以仅填作业i的编号。

图9.7.1　Gantt图

在Gantt图上，一种可行的调度方案应保证各方框的位置满足操作优先的顺序要求，并且同一作业的方框之间不发生重叠。JSSP的处理准则是寻找出总的处理时间最短的Gantt图。

2.简单GA求解举例

考虑一个6×6（用6台设备处理6件作业）问题，作业i的第j操作在设备k上执行的时间为tijk，作业的技术顺序和操作时间如表9.7.2所示，作业的约束条件是一般JSSP的约束条件，即每台设备不能同时处理两项以上的作业，每项作业不能同时在两台设备上处理。各作业的操作之间有优先次序的要求。

表9.7.2　一个6×6的JSSP例子

1）GA的编码方法

用GA求解JSSP，首先要给出初始的染色体种群，为此先要确定染色体的编码方法。编码可以用十进制数码也可以用二进制数码。二进制数码比较简单，但染色体的长度较长，求解以后还要把用二进制数码表示的基因型转换成用十进制数码表示的表现型。不过通常使用较多的还是二进制码。

我们知道，JSSP的解表示成Gantt图形式，它是一种以设备为基础的作业次序时间安排。在本题中每一台设备上要安排6个作业，各个作业有不同的操作时间。所求调度解，应在满足约束条件的前提下使完成全部作业的总时间最少。

我们采用二进制数码来表示种群。为了反映作业操作的优先顺序，采用一种JSSP的“位表示法”，如图9.7.2所示。

图9.7.2　一种JSSP的有限序列位表示法（注：“＜”表示优先于）(www.xing528.com)

图中“作业1＜作业2”表示作业1优先于作业2，该行后面的位序按作业1使用的设备顺序排列。例如作业1的设备顺序按题所定为设备3→设备1→设备2→…。按照这一顺序，比较作业1的各操作是否优先于作业2：若是优先，则用代码1表示；若是相反，则用0表示；若无优先级要求，则用*表示。这样，6台设备就产生了一个6位的位序列。其他作业的位序列图也可类似地产生。

图中有代码1和0的地方，是问题给定的优先级约束条件，而符号*则表示无相应的优先级要求。如果没有任何优先级要求则全部代码都是*。不过规定了技术顺序，常相应地给定了某些优先级要求，例如作业1的第1操作是在设备3上执行的，而作业2的第2操作也是在设备3上执行的，所以设备3对作业1和作业2的优先关系而言，最好是作业1优先于作业2，也就是要用代码1表示。当然，由于某种原因，也可以要求给定相反的优先关系。这样，在编排Gantt图时，为了满足这样的要求就会占用较多的总作业时间。

图9.7.2所示的一个矩阵代码就代表了种群中的一个染色体（二维代码），此时图中*符号，全部用1或0代表。若干个如图9.7.2所示的矩阵就构成了初始染色体种群。

2）从基因型到表现型的转换

有了染色体种群以后，便要对其进行适应度计算，以便优选下代品种，并进行遗传操作（复制、交换、变异）。所有这些计算的前提是要确定染色体从基因型到表现型的转换。具体的遗传操作可以参见前述方法，此处不再赘述，以下仅介绍从基因型到表现型的转换。

在本例中，基因型就是图9.7.2所示的“位表示法”矩阵，而表现型则是与其相对应的Gantt图。为了进行这一转换，先要把“位表示法”矩阵转化成如图9.7.3所示的基于设备的作业顺序矩阵。例如，图中第一行表示在设备1上进行作业的顺序是：

图9.7.3　基于设备的作业顺序矩阵

作这样转换的好处是明显的。因为图9.7.2的“位表示法”中有15个6位序列，其总长度是90，这种基于位序列表示的候选解的数目是290≈1027，而基于图9.7.3所示的作业顺序矩阵表示的候选解的数目是（6！）6≈1017，这个数目比1027小了许多。

那么如何完成这一转换呢？下面给出一个简便的方法假定表9.7.3给出了一个优化解的基因型，其中每一行均按相应作业号的技术顺序排列，各基因位用二进制代码表示，代码1表示有相应的作业优先顺序，代码0表示相反的优先关系。先把图9.7.2改变成表9.7.3，该表是以设备为基础的各作业优先级的代码表示图。图中把设备号顺次列出（不以作业的技术顺序列出），并将各作业的相互优先关系全部列出。显然在每个作业栏中每一纵列中代码1的个数，就表示了在该设备上作业的顺序。例如，对设备1而言，在第1纵列中，作业1的代码1为5个，作业4的代码1为4个，作业3的为3个，作业6的为2个，作业2的为1个，作业5的为0个，所以基于设备1的作业优先顺序为1→4→3→6→2→5。同理，基于设备2的作业优先顺序为2→4→6→1→5→3……最后便得到完整的基于设备的作业顺序矩阵图，如图9.7.3所示。

表9.7.3　基于设备的作业顺序基因

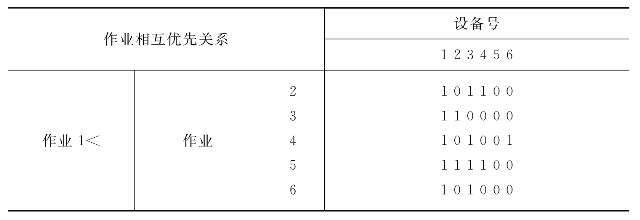
续表

有了图9.7.3所示的基于设备的作业顺序矩阵，就可以根据问题给定的各作业在各设备上被处理的时间tijk来排出Gantt图，但要保证各方框相对同一作业号i不重叠，同时使总的作业时间最短。这一转换是一个比较困难的数学问题。从图9.7.3可知，如果不考虑上述约束条件，则候选解的数目是（6！）6≈1017，这是一个巨大的数目，考虑了约束条件后，虽然这个数目会减少很多，但仍然是较大的数目，在其中又要求出使总的作业时间最短的解，可见这本身就是一个难度较大的优化问题。许多研究者对此进行了研究，提出了一些研究方法，例如文献介绍的全局调和（GH）算法。限于篇幅，此处仅列出研究的结果，而略去方法的介绍。根据图9.7.3及约束条件（各方框相对同一作业号不重叠）文献给出的本例题的优化解如图9.7.4所示。

图9.7.4　最优调度（总作业时间最少）