文献[48]对一个n个城市的TSP问题做了实验验证,所采用的遗传算法框图如图9.6.1所示。

图9.6.1 求解TSP问题的遗传算法框图
该例采用n城市的遍历顺序编码法,适应度函数取总长度T的倒数(无惩罚函数)。选择机制是保留M个较优个体,在每一代运算中,个体被选中的概率与其在群体中的相对适应度成正比。交换操作采用修改的OX法。此法的重点举例如下。
(1)在串中随机选择交配区域,如两父串及交配区选定为
A=12|3456|789
B=98|7654|321
(2)将B的交配区域加到A的前面(或后面),A的交配区域加到B的前面(或后面)得到
A'=7654|123456789
B'=3456|987654321
(3)在A'中从交配区域后依次删除与交配区相同的城市码,得到最终的两个子串为

在本实验中,变异操作的概率很小,一旦发生,则用随机方法产生交换次数K,对所需变异操作的串进行K次对换(对换的两个码位也是随机产生)。
引入逆转操作,对于给定的串,随机给定两个逆转点,在两逆转点之间进行逆转,若逆转后适应度提高,则执行逆转。如此反复,直至不存在这样的逆转操作为止。这一操作,可以改良它的局部极点。(https://www.xing528.com)
实验在386微机上进行,群体规模定为100,交换概率为0.95,变异概率为0.003,初始群体由随机法产生。实验结果表明:
(1)当n≤15时,本算法可以100%搜索到穷举法求得的最优解;
(2)当15<n≤30时,本算法能收敛到“最好解”(难以确认其最优性);多次实验误差结果为0;与模拟退火法相比,时间约为模拟退火法的1/6;
(3)对n=50,n=60,n=80及n=100,…的测试结果表明,遗传算法在求解质量上略优于模拟退火法(SA),优化效率则大大高于模拟退火法,如表9.6.1所示。
表9.6.1 SA法和GA法求解TSP问题的实验结果
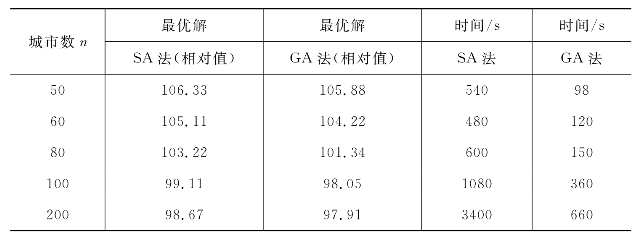
表中所列TSP路径长度为相对长度,其值计算公式为

式中:T d为实际路径长度;X为包含TSP所有城市的最小正方形的边长;n为TSP问题的城市数目。图9.6.2为城市规模n=100的TSP问题的初始群体的路径,图9.6.3为经遗传算法优化后得到的最佳路径。

图9.6.2 100城市TSP问题的初始路径(G=0代)

图9.6.3 100城市TSP问题经遗传算法优化后得到的最佳路径(G=200代)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




