广义背包问题及解决方法

1.0/1背包问题

设有尺寸为S1，S2，…，Sn的n个物体及容量为C的背包，此处S1，S2，…，Sn和C都是正整数。要求找出n个物体的一个子集，使其尽可能多地填满容量为C的背包。

上述背包问题（knapsack problem）的数学形式如下：

式中：Xi表示物体i是否在所选的子集中，若是，则Xi=1，否则Xi=0。

2.广义背包问题(www.xing528.com)

已知两个向量：S=（S 1，S2，…，Sn），P=（P1，P2，…，Pn）及常量C。设X为一整数集合：X=｛1，2，3，…，n｝，T为X的子集。广义背包问题就是找出满足约束条件，而使目标函数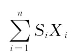最大的子集T，即求Si和Pi的下标子集。其数学形式如下：

广义背包问题可以有不同的应用场合。例如可应用在经济活动中求最大收益的资源有效分配。此时，S的元素是n项经营活动各自所需的资源消耗，C是所能提供的资源总量，P的元素是人们从每项经营活动中得到的利润或收益，则背包问题就是在资源有限的条件下，追求总的最大收益的资源有效分配。

显然，在广义背包问题中，若P=S，则广义背包问题便简化为0/1背包问题。

背包问题在计算理论中属于NP-完全问题，其计算复杂度为O（2n）；若允许物件可以部分地装入背包，即允许Xi可取0.00到1.00闭区间上的实数，则背包问题就简化为极简单的P类问题，此时计算复杂度为O（n）。