使用赌轮方法选择个体的优缺点

遗传算法中的遗传操作是实现优胜劣汰进化的一个关键过程，通过遗传操作，问题逐代优化，最后逼近最优解。

遗传操作包括三个基本的遗传算子（genetic operator）：①选择（selection）；②交换（crossover）；③变异（mutation）。本节讨论选择，以后再逐节讨论其他两个算子。

选择操作又称复制或再生（reproduction），其目的是把优化的个体直接遗传到下一代或通过配对交换产生新的个体再遗传到下一代。选择操作是以个体适应度的计算为基础的，目前常用的方法有以下几种。

1）适应度比例法（fitness proportional model）

这种方法是目前最常用的方法，也称赌轮或蒙特卡罗（Monte Carlo）法。该方法的基本原则是：个体被选择的概率和其适应度成正比。

设群体大小为n，个体的适应度为fi，则i被选择的概率为

当各个个体的被选择概率计算出来以后，在决定哪些个体被选出时，可以用赌轮方法（见图9.3.5）。即把各个个体按概率p i在转轮上划分成扇形区域，使转轮随机转动，转轮停止时，指针所指的扇区，就表示其相应的个体被选中。转轮要转动n次，个体i指定几次，就意味着被选中几次。若转动n次，一次也没有被指到，就意味着该个体应被淘汰。图9.3.5表示了一个有14个个体的赌轮选择方法，该赌轮转动14次，各扇形被指针指到的次数，就是对应的个体被选中的次数。

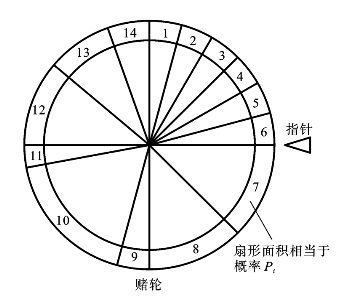
图9.3.5　使用赌轮方法决定被选择的个体

为了避免早熟收敛和随机漫游现象，常对原适应度作定标处理，然后根据定标的适应度计算被选择的概率pi和使用赌轮方法。

2）最佳个体保存法（elitist model）

将群体中适应度最高的个体不进行配对交换，而直接复制到下一代中，此种操作又称拷贝（copy）。

采用这种选择方法的优点是，进化过程中某一代的最优解可不被交换和变异操作所破坏。但也使获得局部最优解的可能性增加。也就是说，该方法牺牲了全局搜索能力，而加快了搜索速度。此法比较适合于单峰性质的搜索问题求解，对于多峰搜索问题要与其他选择方法结合使用。

3）期望值方法（expected value model）

采用赌轮方法时，可能会产生随机误差，也就是说，适应度高的个体也可能被淘汰，适应度低的个体也可能被选中。这种误差在群体数较大时更易发生，因为每个个体被选中的概率pi都较小。为了克服这种误差，可采用期望值方法。期望值方法的基本思想已在9.2节的实例中表述过了，此处再系统地加以总结。

（1）先计算适应度的期望值

(www.xing528.com)

（2）再计算群体中每个个体在下一代生存的期望数

（3）按四舍五入的原则将圆整为整数Ri，Ri即个体i被选中的个数（复制的个数）。若Ri=0（即R＜0.5），则个体i被淘汰。

Dejong曾对以上三法的遗传算法性能进行过对比，实验表明，采用期望值法的遗传算法，其离线性能与在线性能均高于采用另外两种方法的遗传算法性能。

4）排序选择法（rank-based model）

这种方法的思想是按适应度的大小顺序排序，然后按序号选择个体及确定个体数目。事先设计好序号选择表，例如对一个n=10的搜索问题，可以设计一张按序选择表如表9.3.2所示。由表可知，选择概率和适应度无直接关系，而仅与序号有关。

表9.3.2　按序选择表

这种方法的不足之处在于要事先确定选择概率和序号的关系（设计按序选择表）。此外，它和适应度比例法一样都是一种基于概率的选择，所以仍有统计误差。

5）联赛选择法（tournament selection model）

此法的操作思想是，从群体中按一定数目（称为联赛规模）随机选择个体，把其中适应度最高的个体保存到下一代。这一过程反复执行，直到保存到下一代的个体数达到预先设定的数目为止。显然，联赛规模不可过大，否则适应度较高的个体保存过多，容易达到局部解。一般联赛规模取2。

6）排挤法（crowding model）

这种方法是一种确定下一代群体的补充方法。通常群体规模n是一定的，但也可以不是常数。在各代中，群体的个数可多可少，就像自然界中一样。但在自然界中，当同一种群大量繁殖时，为争夺有限的生存资源，该种群中的个体之间的竞争压力必然加剧，因此个体的寿命和出生率也因此降低。排挤法即基于这一思想，在同一种群中，排挤掉相似的旧父代个体。从而提高群体的多样性。具体操作过程如下：

（1）确定排挤参数（CF，crowding factor）；

（2）从群体中随机挑选CF个个体组成个体集（新的个体不包括在内）；

（3）从个体集中淘汰掉一个个体，该个体与新个体的海明距离最短。

以上操作中的新个体是由其他方法决定的。这种方法决定的下一代群体的规模可能有增有减，其最大的优点是能保证群体的多样性。

以上介绍的是目前常用的几种选择方法。每种方法对遗传算法性能的影响各不相同。在具体使用时，应根据实际情况采用较合适的方法，或者把它们结合起来使用。