编码在优化控制及多维问题中的应用

1.编码与映射

实际问题用遗传算法求解时，首先要把实际问题的有关参数，转换成遗传算法空间的代码串（染色体），这一转换操作称为编码（coding），也可以称为表示（representation）。当用GA方法求得最优解时，还要把这个用代码串表示的最优解再转换成实际问题的相应参数，这一逆转换操作称为译码（decoding）。

从数学角度看，编码是由问题空间向GA空间的映射，而译码则是由GA空间向问题空间的映射。在图9.3.1中，问题空间中的参数（个体，又称表现型）为A、B，通过虚线映射为GA空间的A＇、B＇（个体，又称基因型）。在GA空间中，个体A＇与B＇可以产生交换、变异，生成新的个体C，再通过虚线箭头表示的逆映射，在问题空间中生成解个体C，这个过程就是译码。

图9.3.1　编码与映射

2.编码规范与编码原理

编码与译码既然是映射与逆映射，为了能求得最优解，显然编码与译码应符合以下规范：

（1）完备性（completeness）　问题空间中的所有点（候选解），都能作为GA空间中的点（染色体）；

（2）健全性（soundness）　GA空间中的染色体能对应所有问题空间中的候选解；

（3）非冗余性（nonredundancy）　染色体和候选解一一对应。

以上规范，只涉及解的存在与否，不涉及GA算法的效率，因此缺乏指导性。为此，De Jong又提出如下两条编码原理：

（4）有意义积木块编码规则所定的编码应当易于生成与所求问题相关的短距、低阶、高适应度的模式（称为积木块）；

（5）最小字符集编码规则所定的编码应采用最小字符集以使问题得到最简单的表示和最自然的处理。

规则（4）是使GA能更有效地产生最优解。但理论上现在还没有可以基于具体问题找到相对应的较好的积木块的编码结构。

规则（5）提供了一种更为实用的编码原则。采用二值编码符合规则（5）的设计思想。

染色体中每个基因位的状态代表了一个最基本的信息单元。例如在一个二值编码系统中，每个基因可以有3个状态：｛0，1，*｝（*表示或0或1），而在十进制编码系统中，每个基因位可以有11个状态：｛0，1，2，…，8，9，*｝。任何一个参数可以用不同的编码系统来编码，表达该参数的总的信息单元数，应为

式中：N是总的信息单元数；l是位数（长度）；s是每位的状态数。

可以证明，表示同一参数时，总的信息单元数最少的“进制”基数为e≈2.718，也就是说“二进制”或“三进制”是较好的。考虑到在二进制编码中，每个基因位可以有3个状态｛0，1，*｝，所以采用二进制编码可以得到最小字符集的编码。

3.编码技术

1）一维染色体编码

所谓一维染色体编码是指问题空间的参数转换到GA空间时，其相应的染色体是由许多位基因一维排列构成的。这里，每个基因位可以用不同的基数或符号表示，如

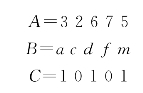
式中：大写英文字母A、B、C表示染色体，它由一系列字符串表示，这些字符串中的每一位称为基因位，可以由十进制数、小写英文字母或二进制数表示。

应用最多的是二进制数表示的二值字符串。在一般情况下，其一维染色体写成如下的字符串

式中A表示用二值字符串表示的一维染色体（个体）；a1，a2，…，a5表示基因，它可以取值1或0。在一般情况下，基因取值与其位置（基因座）有关，即不同位置取不同值就是不同的字符串。如果基因值与基因座的位置无关（在自然界，生物染色体是如此的），这种编码就是重置编码。

2）多参数映射编码

当优化的系统参数为多个时，就要应用多参数编码。例如在如图9.3.2所示的倒立摆系统中，其优化控制参数有3个。

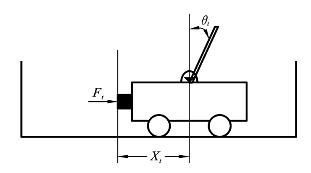
图9.3.2　倒立摆(www.xing528.com)

Xt：小车的速度。

θt：摆倾斜角度。

：摆的角速度。

对此类问题编码时，应将每一个参数都进行二值编码，得到一个子串，然后再把这些子串连接起来，形成一个完整的染色体。

在形成子串时，参数U的范围［Umin，Umax］应该正好落在子串的最大值与0之间。以子串长度l=4为例，便有下列映射关系：

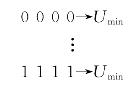
所以任何参数U，对应的二值编码的数值u为

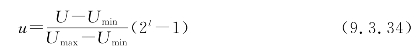
编码精度∏的计算式为

以图9.3.2所示倒立摆为例，若各子串长度l均为4，三个参数对应的二值编码为：，则完整的染色体为12位二进制码串，其中包括3个子串，分别对应于Xt、θt、˙θt，即

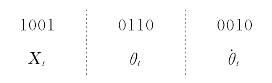
一般而言，在多参数编码中，各子串的长度可以不同，各子串对应的参数范围也可以不同。

3）变长度编码

在自然界里，生物在进化过程中，染色体的长度不是固定不变的。根据这一思想，在遗传算法中引入了变长度编码。变长度编码常常是由于相配的两个父代个体在不同的交换点处切断与拼接而造成的。例如在图9.3.3所示的例子中，两个亲代个体的长度均为9，但由于交换点在不同的基因座处，经过切断和拼接后形成的子代染色体长度分别为6和12。

图9.3.3　切断与拼接后形成不同长度的子代

4）二维编码

当求解的问题是二维或多维时，若采用一维编码就很不方便，尤其是交换操作很不直观。在这种场合，宜采用二维或多维编码。

例如一维图像可以看作是像素在一维空间的排列，每个基因对应一个像素，这样就得到一个二维的基因座的排列（矩阵），如图9.3.4所示。

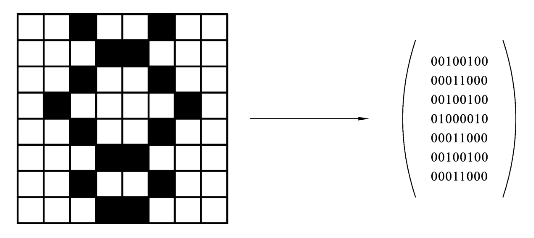
图9.3.4　二维图形与其对应的二位编码

在自然界中，单倍体（haploid）是最简单的染色体结构，多出现在不太复杂的低级生物体中。而在高级生物体中，则多含有较复杂的二倍体（diploid）或多倍体（polyploid）的染色体结构。例如，其下所示为二倍体结构染色体：

AbCDe

aBcde

每个字母代表一个基因位，大写字母表示显性基因，小写字母表示隐性基因。所谓显性与隐性，在生物学上是指在染色体的表现型中，基因的性质是否能表现。例如上述二倍体的表现型为

ABCDe

我们可以看到，显性基因总是被表现，而隐性基因只有当两个同型染色体中的等位基因皆为隐性基因时才能被表现。

生物体为什么采用这种冗余的信息编码结构及显性算子的屏蔽保护技术，至今仍是遗传学遗留的问题。有一种遗传学的解释是：二倍体这种结构及显性规则，保护了被记忆的曾经有用的基因免受有害选择所破坏。自然界的生态环境常发生或大或小、或好或坏、或快或慢的变化，有生命力的生物应能迅速适应环境的变化，二倍体结构能提供冗余的记忆能力，而显性基因则能唤醒对旧知识的记忆，验证一下旧知识的效果，因而能表现更强的自适应环境的能力。

编码方法对遗传算法有很大的影响，要结合具体问题来考虑。在大多数情况下，一般多用二进制编码，对多参数问题，常用不同长度子串连接的多参数编码法，在二维问题中，多采用二维编码（平面编码）。

除了以上介绍的编码方法外，还有树结构编码、非二值编码、带有修饰基因的二倍体编码法等，此处不再一一介绍了。