模糊Hopfield网络的优化研究

模糊数学与系统的问题，常可用神经网络的方法来求解。本节介绍模糊Hopfield网络，用模糊等价关系来求解模糊聚类问题。

模糊Hopfield网络，从结构方面看，基本上就是离散型Hopfield网络。两者的区别在于：

（1）模糊Hopfield网络是具有自反馈的全互连网络，而离散型Hopfield网络则可以是无自反馈的非全互连网络。

（2）模糊Hopfield网络中各神经元之间的连接权重Wij用模糊相似关系（rij）n×n来表示，而离散型Hopfield网络的连接权重Wij则由样本的学习决定。

（3）模糊Hopfield网络中能量函数的定义与离散型Hopfield网络不同，前者由模糊相似关系决定，后者则由连接权重Wij决定。

（4）模糊Hopfield网络神经元的“净输入”运算采用模糊并（∪）运算，而离散型Hopfield网络神经元的“净输入”运算则采用求和累加（Σ）运算。

图8.6.5表示了模糊Hopfield网络，它是一个连接权重为（rij）n×n的全互连自反馈网络。该网络可以用如下的五元组表示其特征：

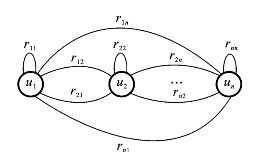
图8.6.5　模糊Hopfield网络

式中：FHN表示模糊Hopfield网络；U表示神经元集合，U=｛ui；R表示神经元互连权重，它由模糊相似关系矩阵组成：R=（rij）n×n∈［0，1］n×n；Λ表示神经元阈值向量Λ=（λ1，λ2，…，λn）T∈｛0，1｝n×1。Y表示神经元输出向量，Y=（y1，y2，…，yn）T∈｛0，1｝n×1。即模糊Hopfield网络的神经元的输出是二值（0或1）输出，用Y（t）表示t时刻模糊Hopfield网络神经元的状态（0表示抑制状态，1表示激活状态），O表示模糊神经网络的复合运算模式，通常多采用“最大-最小模型”（见式（8.6.3））或“最大乘积模型”（见式（8.6.4））。用向量形式可以写成

模糊Hopfield网络的神经元模型如图8.6.6所示。图中yj（j=1，2，…，n）表示第j个神经元u j的输出；λj（j=1，2，…，n）表示第j个神经元的阈值；∪表示并运算（最大-最小模型或最大乘积模型）；f表示截集运算。

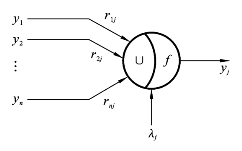
图8.6.6　模糊Hopfield网络的神经元模型

模糊Hopfield网络的工作很简单，首先按给定的几个模式计算其相似矩阵：R=（rij）n×n。按R给定网络的初始权重，再给定阈值Λ=（λ1，λ2，…，λn）T（一般是相同的值）和初始状态yi（0）（i=1，2，…，n），然后网络便可自动迭代，达到稳定状态时，各神经元的稳态二值输出即等价关系的聚类结果。

现在要证明模糊Hopfield网络最多经过n次迭代就能由初始状态收敛至稳定状态。

对于n阶模糊Hopfield神经网络〈U，R，Λ，Y，O〉，其能量函数可以仿照离散型Hopfield神经网络来定义，用向量形式可以写成

若有

即

则称网络达到稳定状态。

我们先证明任一神经元ui的输出yi（t）一旦取1值后，在下一时刻（t+1）及以后的各个时刻均不会改变，也就是说下述定理成立。

定理8.6.1　设有n阶模糊Hopfield神经网络〈U，R，Λ，Y，O〉，待分类的模糊集合X=｛xi|1≤i≤n｝，R为X×X上具有自反性的模糊关系，则对于任一时刻t，

成立。

证明　由R的自反性可知，∀i∈｛1，2，…，n｝，

对于任一时刻t，若yi（t-1）=1，则

即　

故　(www.xing528.com)

若　

则　

定理8.6.2　设有n阶模糊Hopfield网络〈U，R，Λ，Y，O〉，模式集合X=｛xi|1≤i≤n｝，R为X×X上具有自反性的模糊关系，则

（1）模糊Hopfield网络是稳定的；

（2）当且仅当能量函数E收敛至某一能量值时，模糊Hopfield网络达到稳定状态；

（3）模糊Hopfield网络最多经历n个时刻，必由初始状态收敛至稳定状态。

证明　采用式（8.6.9）形式的能量函数，若能证明在迭代过程中，其网络的能量是不断增加的，但又有界，则网络的能量函数必须收敛于某一能量值。

又

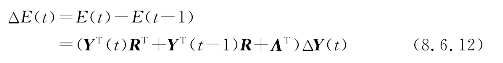
故由定理8.6.1知

即能量函数E将收敛至某一能量值。由λi＞0（λi∈Λ），故由式（8.6.12）知，当且仅当ΔY（t）=0时E收敛。故

（1）若∀i∈｛1，2，…，n｝，ΔYi（t）=0，则网络达稳定状态。

（2）若∃i∈｛1，2，…，n｝，ΔYi（t）≠0，这种情况只有在ΔY i（t-1）=0时才有可能，而当ΔY i（t）=1时，由定理8.6.1知

于是网络也达到稳定。以上情况，最多经历n个时刻，所以对整个网络而言，最多经过n个时刻后，由于ΔYi（t+1）=0，所以网络处于稳定。

例8.6.1　设有论域X=｛x1，x2，x3，x4，x5｝及X×X上的模糊相似关系：

构造模糊Hopfield网络〈U，R，Λ，Y，O〉。

（1）令模糊Hopfield网络的各神经元连接权重等于R，λ=0.5，模糊Hopfield网络神经元的初始状态为e1=（1，0，0，0，0），e2=（0，1，0，0，0），则模糊Hopfield网络聚类结果如表8.6.1所示。

表8.6.1　λ=0.5时的聚类结果

由表8.6.1可知，模式集合X中的元素被分成两类：｛x1，x3，x4，x5｝，｛x2｝。

（2）令λ=0.6，模糊Hopfield网络聚类结果如表8.6.2所示。

表8.6.2　λ=0.6时的聚类结果

由表8.6.2可知，当λ=0.6时，模式集合X中的元素被分为三类：｛x1，x3｝，｛x2｝，｛x4，x5｝。

（3）令λ=0.7，模糊Hopfield网络聚类结果如表8.6.3所示。

表8.6.3　λ=0.7时的聚类结果

由表8.6.3可知，当λ=0.7时，模式集合X中的元素被分为四类：｛x1，x3｝，｛x2｝，｛x4｝，｛x5｝。