最基本的模糊神经元与普通神经元有相似的地方,也有相区别的地方。从结构与功能看,两者都是多输入单输出的单元;在单元内部对输入信息进行非线性(包括线性)处理;单元与单元之间有相互作用(激活或抑制),用连接权重来表示,如图8.6.1所示。
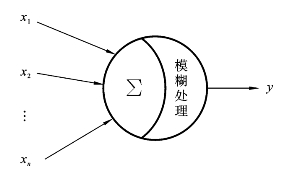
图8.6.1 模糊神经元的基本模型
模糊神经元与普通神经元的基本区别在于前者输入、输出均是模糊信息,单元内部的加权和信息处理都带有模糊性质,处理的数学方法也是模糊数学的基本方法。根据输入、输出信息的不同及处理的模糊方法的不同,模糊神经元又分为以下几种类型。
1)广义合成运算模型
这种模型的特点是模糊处理运算采用广义模糊合成运算,如图8.6.2所示。当输入是向量![]() 时,处理单元相当于一个模糊关系
时,处理单元相当于一个模糊关系![]() (rij)n×l,输出量是向量
(rij)n×l,输出量是向量![]() 。
。
这类神经元的输出![]() 可以由模糊复合运算决定。
可以由模糊复合运算决定。

图8.6.2 第一类模糊神经元模型
![]()
或者写成向量形式

常用的是“最大-最小模型”,即
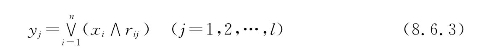
或者用“最大乘积模型”,即
 (https://www.xing528.com)
(https://www.xing528.com)
有时也用“加权平均模型”,即

2)模糊隶属度模型
这种模型的特点是输入信息的加权操作,就是求得其相应的隶属度,如图8.6.3所示。
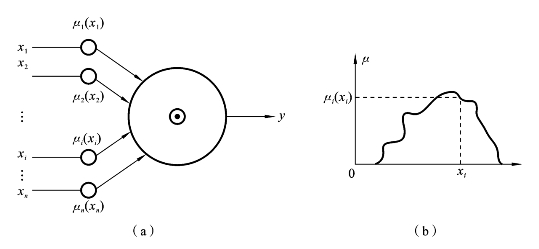
图8.6.3 输入信息的隶属度与相应的第二类模糊神经元模型
设xi是神经元的第i个输入信息,μi(·)是第i个权的相应隶属度函数,y是神经元的输出,![]() 表示模糊算子,则其输出y的数学表达式为
表示模糊算子,则其输出y的数学表达式为
![]()
3)全模糊量模型
这种模型的特点是输入为模糊集,加权是对整个隶属函数进行操作,单元内的运算也是模糊运算,如图8.6.4所示。
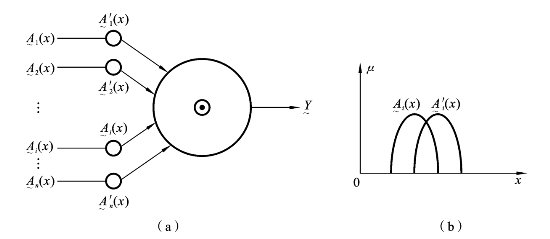
图8.6.4 隶属度函数整体加权与第三类全模糊量神经元模型
设输入信息是模糊集,其隶属函数是Ai(x)(i=1,2,…,n),加权处理针对地是整个隶属函数,处理后的隶属函数是A'i(x)(i=1,2,…,n),![]() 表示模糊算子,则输出亦为模糊集
表示模糊算子,则输出亦为模糊集
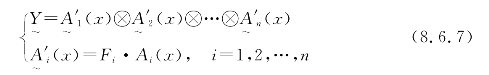
式中:Y是神经元输出模糊集;![]() 分别是加权前和加权后的第i个输入模糊集隶属函数;Fi是对第i个模糊集输入的加权操作。
分别是加权前和加权后的第i个输入模糊集隶属函数;Fi是对第i个模糊集输入的加权操作。
以上三种类型的模糊神经元,仅从功能和结构上进行分类。在实际应用中,由于一个模糊集要用隶属函数来表示,即要用许多数来表示,而每一个数(隶属度)又都要参与运算,所以还要把上述功能性的神经元再分解成若干基本运算的神经元。每一个基本运算的神经元,仅计算模糊集隶属函数运算中的一个点,若干个这样的神经元才组成一个功能神经元。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




