优化多层前馈随机网络的标题

1985年，Hinton等人借助统计物理学的概念和方法，提出一种多层、有教师学习的前馈网络，称为多层前馈随机网络，也称Boltzmann机网（BM网）。

此网络的工作原理与前述多层前馈网络相同，即先输入网络的一个样本，激活给定的输入层单元及输出层单元，然后修改连接权重。不同处在于：在多层前馈网络中，是根据误差来调节权重的，而在BM网中，则是按温度T不断减小，总能量趋向最小时的状态概率分布来调节权重的。后者由于是按随机状态来调节的，因此可以避免局部最小，达到能量函数的全局最小。

设三层BM网模型如图8.5.2所示。各处理单元间为确定连接（也有的Boltzmann机各神经元之间为随机连接），输入单元为ai，隐含层单元为bj，输出单元为ct，（其中i=1，2，…，n；j=1，2，…，p；t=1，2，…，q）。输入层至隐含层单元的连接权重为Wij，隐含层单元至输出层单元的连接权重为Wjt，输入学习样本是X=（x1，…，xi，…，xn），Y=（y1，…，yt，…，yq），分别激活相应的输入单元ai及输出单元ct。

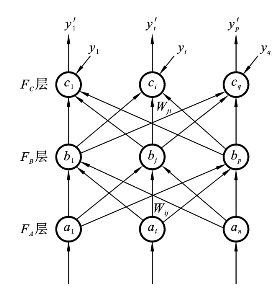
图8.5.2　三层BM网模型

BM网的学习算法如下：

1.第一阶段

由样本确定输入、输出层单元的正确状态。

1）初始化

随机确定FA与FB层间的连接权重Wij及FB层与FC层之间的连接权重Wjt，取值范围［+1，-1］。

2）起始时刻t=1

①输入样本X=（x1，…，xi，…，xn），Y=（y1，…，yt，…，yq），分别激活相应的ai，ct。

②随机选择FB层处理单元的状态b j=｛0，1｝（即单元j的输出）。

③计算全局能量及能量变化：全局能量为（略去偏流与阈值）

在隐含层中，使任一单元bj状态变化，此时所引起的全局能量变化为

④计算由ΔEj引出的Boltzmann概率分布为

式中：T（t）是随时间变化的正值温度系数。

如果ΔEj＞0，pj＜r（r是某个选定的概率），说明改变了的bj状态出现的概率很小，bj状态不应改变，所以将bj的状态还原到原来的状态（步骤②）。

⑤选择FB层中一个新的处理单元b，重复步骤②～④，直到全部隐含层单元状态确定为止。(www.xing528.com)

⑥增加t到t+1。计算新的温度值为

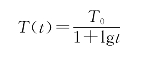
式中：T0为起始温度。

⑦重复步骤②～⑥，直到对所有FB层单元均有ΔEj=0，此时网络可实现全局能量最小。

此时FB层所有单元的输出值b j（j=1，…，p）构成一个矢量Dk（脚标k表示第k次迭代），k=1，2，…，M（共有M次迭代）。在bj的状态下，FC层各单元被钳制到一个正确的给定状态。

3）计算对称概率Pij和rjt

根据Dk，计算FA层第i单元与FB层第j单元的对称概率pij表示为

式中：Φ定义为

同理，计算FC层第t个单元与FB层第j个处理单元的对称概率rjt可表示为

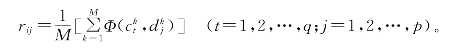
2.第二阶段

仅钳制输入层单元为样本给定状态，输出层单元自由。

①重复第一阶段各步骤，使网络再次达到温度最低的平衡状态。

②按第一阶段的公式分别算出各层的对称概率p＇ij、r＇jt。

③调整连接权重。利用下述公式计算连接权重的调整值

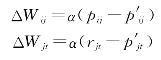
式中：α为学习速率，取正的常数值。

④重复第一、第二阶段各步骤，直到ΔWij、ΔWjt→0时为止。

BM网学习算法比较复杂，计算过程较长，网络要通过多次迭代才能收敛，总的收敛时间很长，但这种算法能够保证网络的能量函数达到全局最小值。