最优线路规划：旅行商问题解决方案

旅行商问题（简称TSP）是一个典型的组合优化问题。该问题是：设有N个城市，要求推销员从某一城市开始，非重复地访问其余所有城市后回到原来出发的城市，问如何优化旅行路线，使其总旅行路程最短。

对于N个城市，不重复地旅行通过所有城市再回到出发地的不同路径可以有（N-1）！/2，在计算每条路径的长度时，需要进行N次相加的加运算，所以解决TSP的总计算量为N！/2，即随城市数N成阶乘关系增长。如果使用运算速度为1亿次/秒的计算机求解，在N=10时，约需1.8×10-2 s，但当N=25时，则需要花费25亿年之久！显然，使用穷举算法来解决较大规模的TSP是不现实的。

现在用Hopfield网络求解。首先采用一个N阶矩阵来表示旅行路径及各城市在旅行中的次序。用矩阵中的行表示城市，用矩阵的列表示旅行路径中的次序。矩阵元素“1”表示访问，“0”表示“不访问”。显然，若矩阵各行各列都仅含一个“1”元素，其余均为“0”元素，则该矩阵描述一条有效访问路径。这种矩阵称为换位矩阵（permutation matrix）。以A、B、C、D、E城市TSP为例，两城市间的距离用dAB、dAC、dBC……表示。图8.3.3（a）表示了一条访问路径：C→A→E→B→D→C，相应的换位矩阵如图8.3.3（b）所示。其路径长度为

图8.3.3　五城市访问路径的换位矩阵表示

这样N个城市N个访问次序就排列成N2个矩阵元素（N行N列），每个矩阵元素相当于一个神经元，各神经元状态取值0或1，于是就用神经元阵列代替了换位矩阵。要求神经元阵列在稳定状态时，每一行的神经单元仅有一个处于“1”状态，其余单元为“0”状态，每一列也只有一个单元为“1”状态，其余为“0”状态。在阵列全部单元中，“1”状态单元的总数为N，这表示每个城市仅访问一次。一个阵列状态图就表示了一条访问路线。这样就为使用神经网络求解TSP作好了准备。

用Hopfield网络来求解TSP时，关键是如何构造能量函数，然后由能量函数再来决定输入的初始权重。当初始权重调整好以后，用偏流si来给定网络初始状态，然后网络便自动向最小能量状态变动，当稳定后，所得到的网络状态就是问题的解。

1.构造能量函数

构造能量函数E，应使其极小值对应于TSP的解。为此，根据TSP的特点，能量函数必须满足如下的要求：

（1）对换位矩阵元素给出一定的约束，在组成能量项时，保证满足这些约束时，能量项为最小值，这时的换位矩阵状态便描述了一条有效访问路径。

（2）能将路程较短的有效访问路径作为TSP的解。

考虑到第一个要求时，可选择TSP的能量函数为

式中：A、B、C均为正值常数。容易看出上式右边第一项是诸行中任意两个不同列的元素乘积之和，由于各元素仅取值0或1，因此只有当换位矩阵中每行中“1”的元素个数不多于一个时，此项才等于零。同样只有当每一列中“1”的元素个数不多于一个时，上式右边第二项才等于零。当路径中访问的城市数（等于矩阵中“1”的元素的总数）恰为N时，上式第三项为零。因此，能量函数E1=0时，将保证矩阵描述一条有效访问路径。

对于第二个要求，需要考虑路径长度信息。从单元（x，i）计算起，计算x城市与y城市的路径时，只有两种可能：一种是（y，i-1）→（x，i），还有一种是（x，i）→（y，i+1）。考虑到这两种情况，可以选择下列能量函数：

式中：D为常数。式（8.3.19）正好表示了访问路径的路程总长度。

将式（8.3.18）与式（8.3.19）合并，构成总的能量函数为(www.xing528.com)

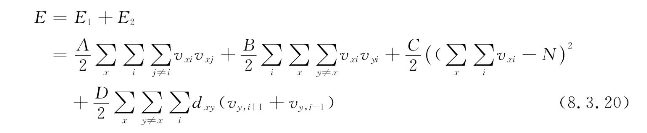
如果系统A，B，C，D取足够大（当访问10个城市时，选用A=B=D=500，C=200），那么所有与低能量E相应的换位矩阵（或神经元阵列）都将描述一条有效的访问路径。最低能量值意味着相应路径长度最短，表示TSP的最优解。

2.组成神经网络

用Hopfield网络来求解TSP。令TSP的能量函数表示式（8.3.20）与连续型Hopfield网络的能量函数表示式（8.3.11）相等，通过比较，可以确定网络神经元连接权重Wij和外部输入的偏置电流si。采用双下标方式表示，其连接权重为

式中：

外部偏置

易知，式（8.3.21）等号右边前面三项体现了TSP解有效性方面的约束，最后一项则体现了“路径长度尽可能短”的要求。

将式（8.3.21）、式（8.3.22）用于式（8.3.7），便得出Hopfield网络求解TSP的动力学方程

式（8.3.25）表示了神经元的非线性特性，其中u0是调节非线性函数的陡度的常数。

对于10个城市A，B，…，I，J的TSP，选用A=B=D=500，C=200，u0=0.02。网络的初始状态是按式（8.3.21）给出权重，再确定从某一城市开始，用式（8.3.23）给出初始输入（即偏流sxi=CN，其余均为0），经过电路的时间常数以后，网络便达到稳定状态。整个收敛过程如图8.3.4所示，图中方块大小与神经元输出成比例。网络收敛后，神经元输出产生一个稳定的换位矩阵（见图8.3.4（d））。由图可知，图示的TSP的优化解为路径：D→H→I→F→G→E→A→J→C→B。

3.神经网络模拟的结果

图8.3.4　TSP神经网络收敛过程

Hopfield曾用900个神经元组成的网络求解30个城市的TSP，路径总数达N=1030，整个网络仅用数秒钟就得到了稳定状态，根据网络动力学方程（8.3.24）及方程（8.3.25），也可以在计算机上模拟神经网络求解TSP。文献［39］给出了应用Hopfield网络在计算机上模拟的程序，有兴趣的读者可以参考此文献。