离散型Hopfield网络简介

这种网络是一种离散的时间动力系统，如图8.3.1所示。

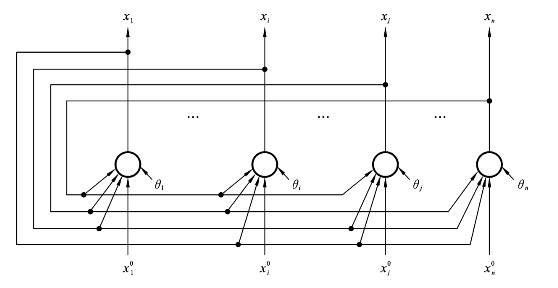
图8.3.1　离散型Hopfield网络

由图可知，网络中每个神经元的输出，都通过连接权重与其余各神经元的输入端连接。输入模式为，其中每个分量均取+1或-1（或1、0两状态）；输出模式（即各神经元的状态）为X=（x1，…，xi，…，xj，…xn）（也取二值）；神经元的个数与输入、输出模式向量的维数相同。样本模式记忆在神经元之间的连接权重上。若有M类模式，并设是第S类样本。为了存储M个类样本，要求存储网络的稳定状态集为｛XS｝，S=1，2，…，M。神经元i和神经元j之间的权重Wij按式（8.3.1）预先设置：

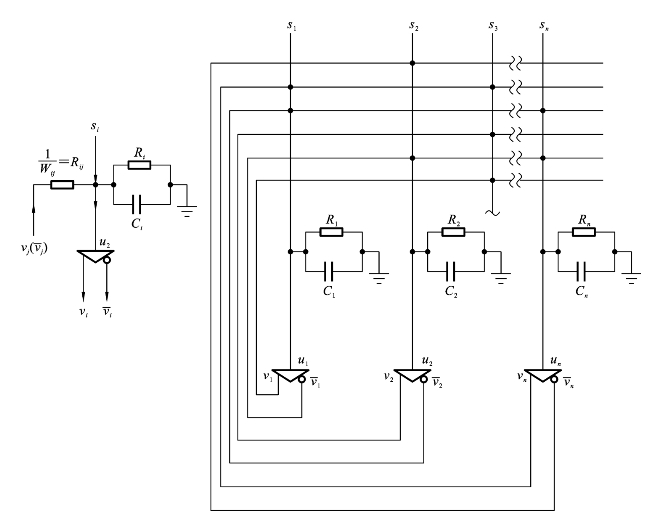
图8.3.2　Hopfield-Tank连续神经网络模型

在连续时间模型中，神经元由电阻、电容和运算放大器组成。各元件的作用以及连接权重的模拟作用如下：

（1）电阻Ri和电容Ci并联，模拟生物神经元输出的时间常数，构成神经元的动态特性。

（2）神经元i和神经元j之间的连接权重Wij，可以看成神经元的输出到神经元的输入之间的互电导，即，它模拟神经元之间的突触特性。

（3）运算放大器具有正、反向输出，用来模拟生物神经元的非线性特性。放大器的“+”输出端和“-”输出端分别模拟生物神经元的兴奋和抑制特性。Wij＞0（对应于兴奋性突触）时，神经元i的输入和神经元j的“+”输出端相接；Wij＜0（对应于抑制性突触）时，神经元i的输入和神经元j的“-”输出端相接。每个神经元的输出（“+”或“-”）通过连接权重与其余神经元的输入连接。(www.xing528.com)

（4）外加偏置电流si，用来建立一般的兴奋电平。

在网络工作前，与离散型的Hopfield网络类似，先要按M个样本的输出状态来给定网络的连接权重。设样本共有M个样本，则神经元i和神经元j之间的权重为

当输入一个待识别模式时（通过偏置电流si给定），网络能从记忆的权重中寻找与输入模式最接近的训练模式，这种“寻找”，就是网络随时间演化不断改变运算放大器的输出状态，最终使网络达到稳定的状态。此时的输出就是与输入的待识别样本最匹配的训练样本。

而且当时，有

这就是说，随着时间的增加，网络总是朝着能量函数减小的方向运动，网络最终会达到稳定的平衡点，也就是E的一个极小值点。

对于理想的运算放大器，网络的能量函数可以简化为

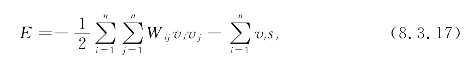
Hopfield神经网络模型的局限性主要有两个方面。其一，网络能够记忆和正确回顾的样本数不能太多，否则网络可能收敛于一个不同于所有记忆样本的伪模式。Hopfield已经证明，记忆不同模式的样本数小于网络神经元数（或模式向量的维数）的0.15时，收敛于伪样本的情况才不会发生。其二，如果记忆中的某一样本的某些分量与别的记忆样本的对应分量相同时，这个记忆样本可能是一个不稳定的平衡点。