改进的BP算法优化探析

以BP算法为基础，约从2010年开始，许多改进算法被提出，列举其中一些重要的算法进行介绍。

1.调节学习速率的快速BP算法（MEBP算法）

在BP算法中，学习速率α、β是不变的，这是造成BP学习算法收敛很慢的一个重要原因。如果网络中各个参数的调节有各自的学习速率，而且这些学习速率在网络学习过程中可以根据误差曲面上不同区域的曲率变化来自适应调节最优学习速率，那么整个网络的学习收敛便会大大加速。在误差曲面的某一区域，若对某一参数而言，误差曲面有较小的曲率，则在这一参数连续几步的调节中，误差函数对这一参数的偏导数一般具有相同符号；若误差曲面相对这一参数有较大的曲率，则在这一参数连续几步的调节中，误差函数对这一参数的偏导数一般具有不同符号。因此，根据误差函数对网络参数的偏导数符号在这些参数连续几步的调节中是否改变，来决定相应参数的学习速率是否增减。

具体算法如下。

（1）作用函数采用双曲正切函数形式，有

则其导数通过计算可得

（2）调整误差δt、δj分别变为

为了书写方便，以下均以隐含层的参数来写，例如对调整误差，均统一写成

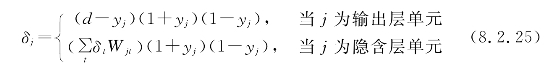
（3）反向调整各层的权重和阈值。在一次学习中，反向调整时按下列公式修正权重：

式中：η1、η2、η3分别为权重、阈值、增益的学习速率（学习步长），只要将η3取为0，Cj初值取作1，则增益就不起作用。

（5）采取改变学习步长的策略。在学习过程中，若本次误差大于上次误差，则这次迭代无效，恢复迭代前的学习速率，减小步长增加的幅度重新迭代；反之则本次迭代有效，增大学习速率。

仿真结果表明，与BP算法相比，在选用相同的学习训练步数的条件下，MBP算法的精度远远高于BP算法的精度（至少高出三个数量级）。若对于相同精度要求，则MBP算法可以在很少的步数内达到精度要求，即收敛速度大大加快。

3.隐含层单元自构形学习算法

在前向网络中，输入层单元数与输出层单元数是由问题本身决定的。但如何确定隐含层单元数就比较困难。隐含层单元数少了，学习可能不收敛，隐含层单元数多了，可能单元冗余，收敛速度减慢。最好的办法是网络在学习过程中，自组织和自学习自己的结构。(www.xing528.com)

这种学习过程分为预估和自构形两个阶段。在预估阶段，根据问题的大小及复杂程度，先设定一个隐含层单元数较多的前向网络结构。在自构形阶段，网络根据学习情况合并无用的冗余单元，删除不起作用的单元，最后得到一个合适的自适应网络。

图8.2.6　隐含层单元i与j的合并

式中：Wbt是阈值θt对应的权重。

从而得合并算法：

（2）删减规则。若Si＜C2，则单元i可删除。

由式（8.2.38）可知，当Si≈0时，可令，则输出层单元t的净输入为

式中：Wbt是阈值θt对应的权重。

所以删减算法为

实际上，删掉的单元i的权重合并到输出层单元t的阈值θt中了，如图8.2.7所示。

图8.2.7　隐单元的删除

当不考虑不同故障单元有不同影响时，上式中的αf=1，这时就出现了模型1的情况。

在设计容错神经网络时，由于冗余是容错的基础，所以在这种网络中，隐含层中的单元数要比不容错的网络为多，一般容错神经网络的隐含层单元数是不容错网络隐含层单元数的1～2倍。