神经网络学习规则详解

学习和记忆是人类智能器官的最主要功能，模拟人脑神经系统的学习功能是人工神经网络的核心任务。

由人工神经元相连接的神经网络系统的全部“知识”，主要体现为网络中全部神经元之间的连接权重。通过一定的规则，根据神经元的输入状态（或活性度）、当时的连接权及有无教师示教的信息来调整连接权重，这就是人工神经网络的学习过程。这里所依据的规则，就称为学习规则。可以说有怎样的学习规则就有怎样的人工神经网络。常用的学习规则扼要说明如下。

1.联想式学习——Hebb规则

心理学家Hebb在1949年提出突触联系的神经群体理论。他指出，突触前、后两个同时兴奋（即活性度高，或称处于激发状态）的神经元之间的连接强度（权重）将增强。虽然他本人没有给出数学表达式，但后来许多研究者用不同的数学公式来表达这一基本思想。Hebb提出的这一原则被称为Hebb规则。

图8.1.5表示了两个相连的神经元之间的信号联系。从神经元ui到神经元uj之间的连接权重为Wij；uj与ui被“激活”的程度aj（t）、ai（t）称为活性度；uj与ui的输出分别为yj与yi；教师的示教信号为tj（t）。

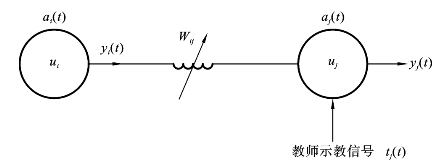
图8.1.5　Hebb规则

输出yi、yj与活性度ai（t）、aj（t）有关，满足如下关系：

其中：fi、fj是传递函数（作用函数）。

对于神经元uj而言，其输入（即ui的输出）yi（t）可以理解为学习的内容，连接权重Wij可以理解为学习的基础，tj（t）是教师的指导内容，uj的活性度aj（t）可以理解为学习的“积极性”。易知，学习的方式和结果与上述四个要素有关。在人工神经网络中，每一次学习意味着一次权重Wij的调整，因此权重变化ΔWij可以用下列函数式表示：

采用不同的函数G和H，就有不同的学习规则。例如，当上述神经元uj上无教师示教信号时，H函数仅与yi成正比，则式（8.1.4）改成简单的形式

式中：η是学习速率常数（η＞0）。

式（8.1.5）表明，对一个神经元uj而言，若该元有较大的活性度或较大的输入（即yi（t））时，它们之间的连接权重会变大。

2.误差传播式学习——Delta学习法则

此时，式（8.1.4）中的函数G采用下列形式：

(www.xing528.com)

其中：η1为正数，把差值（tj（t）-aj（t））称为δ。

函数H仍与神经元ui的输出yi（t）成正比：

其中：η2为正数。

根据Hebb规则可得

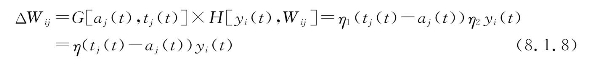
在式（8.1.8）中，如将教师示教信号tj（t）作为期望输出dj，而把aj（t）理解为实际输出yi，则该式变为

式中：δ=dj-yj为期望输出与实际输出的差值。称式（8.1.9）为δ规则，又称误差修正规则。根据这个规则可以设计一个算法，即通过反复迭代运算，直至求出最佳的Wij值，使δ达到最小。这个规则就是BP（反向传播）网络的算法基础。

从上述简化过程可知，在选用简化的G函数时，我们实际上令yj=aj（t），也就是用了线性可分函数。故式（8.1.9）不适用于采用式（8.1.3）的非线性传递函数的情况，此时就需采用广义的δ规则（1986年，Rumelhart和Hinton等人总结），这将在BP网络节中详细介绍。

3.概率式学习

网络包括输入、输出和隐含层，但隐含层间有互连。这种网络基于统计力学、分子热力学和概率论中关于系统稳态的能量标准进行学习，称为概率式学习。典型的代表是Boltzmann机学习规则。这种网络的学习过程是根据神经元i和j在不同状态时实现连接的概率来调整其间的权重：

式中：分别是神经元i和j在输入、输出固定状态及系统为自由状态时实现连接的概率。调整的原则是：当时，增加权重；否则减小权重。

4.竞争式学习

这种学习是无教师示教学习。网络分成不同的层，网络中的神经元之间分成兴奋性连接和抑制性连接。在不同的连接机制中引入竞争。竞争的实质是看哪个神经元受到的刺激最大，由此来调整权重：

式中：Cik为外部刺激k系列中第i项刺激成分；nk是刺激k系列输入单元的总数。

在竞争中，与输入单元间连接权重变化最大的为优胜者，优胜者的连接权重按式（8.1.11）改变，而失败的单元其ΔWij为零。