1.判断与推理
人们的思维就是利用概念来进行判断和推理。判断是概念与概念的关联,而推理则是判断与判断的联合。如果概念是模糊的,则判断和推理就是模糊的。
若用符号及其运算来表示思维的过程,就称为思维的形式化。我们的目的,就是要寻求符合思维实际情况的思维形式化的规律与方法。
1)判断句
判断句的句型是“x是A”,其中A是表示概念的一个词或词组,也就是在论域X上的一个集合,x表示论域X中的任何一个特定对象,称为语言变量。如果A的外延是清晰的,则A所对应的集合是普通集合,若A的外延是模糊的,则A对应的集合是模糊集合。将判断句“x是A”简记作(A)。当A为普通集合时,称(A)是普通判断句;当A是模糊集合时,称(A)是模糊判断句。
在二值逻辑中,如果x∈A,则称(A)的判断为真,A就是(A)的真值域;如果x![]() A,称(A)为假。如图7.8.5所示,图中阴影部分表示(A)为真,是判断(A)的真值域。显然有
A,称(A)为假。如图7.8.5所示,图中阴影部分表示(A)为真,是判断(A)的真值域。显然有
![]()

图7.8.5 判断(A)的真值域
在模糊逻辑中,“x是A”的判断没有绝对的真假,将x对的隶属度定义为(A)判断句的真值。
![]()
例如“x是菱形”“x是人”是普通判断句;而“x是晴天”“x很暖和”就是模糊判断句。
2)推理句
“若x是A,则x是B”型的判断句,称为推理句,简记为“(A)→(B)”。若A、B为普通集合,则称此推理句为普通推理句,若A、B为模糊集合,则称此推理句为模糊推理句。
例如,“若x是菱形,则x是平行四边形”是普通推理句,因为“菱形”“平行四边形”这些集合是普通集合;而“若x是晴天,则x很暖和”就是模糊推理句,因为“晴天”“暖和”这些集合是模糊集合。
3)推理句的形式化
用符号及运算来表示推理句的过程,称为推理句的形式化。当然这种形式化必须符合推理的真实含义。
在普通集合范围内来考虑“x是A,则x是B”这一推理句,我们可用前述定义的符号来代表有关的判断句,即“x是A”用(A),“x是B”用(B),“x是A,则x是B”用(A)→(B)来表示。对论域中的所有x进行上述推理句考察时,可以分成四种情况:
(1)(A)是真同时(B)也是真,当然(A)→(B)为真。
(2)(A)是真但(B)是假,显然(A)→(B)不成立,即为假。由于(A)为假时(即x不在A中),推理句中没有限制“x是B”或“x不是B”,也就是说(B)为真或为假都可以,即此时(A)→(B)都能成立(为真)。
(3)(A)为假,(B)为真时,(A)→(B)为真。
(4)(A)为假,(B)为假时,(A)→(B)为真。
举一例来说明上述推理,更易理解,例如有下列推理句:
“如果今天下雨,我就在家中。”
显然有:①“如果今天下雨,我就在家”这是真的;②“如果今天下雨,我不在家”是假的;③“如果今天不下雨,我也在家”,这也是可以的(真的);④“如果今天不下雨,我不在家”,这也是可以的(真的)。这是因为③、④两种情况,推理句没有限制,即如果不下雨,我可以在家也可以不在家。
根据上述分析,我们可以作出如表7.8.5所示的真值表。
表7.8.5 蕴涵式(A)→(B)的真值表

根据此真值表,我们可以得出如下推理的形式化模型:
![]()
或将式(7.8.5)简写成
![]()
这就是二值逻辑中归约律的情况。
若令A→B=C,则普通推理句“(A)→(B)”等价于一个判断句“x是c”,即
![]()
![]() 的真值域如图7.8.6所示。为了便于推广到模糊推理的情况,常把式(7.8.6)写成相应真值的等式:
的真值域如图7.8.6所示。为了便于推广到模糊推理的情况,常把式(7.8.6)写成相应真值的等式:
![]()
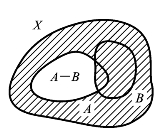
图7.8.6 ![]() (https://www.xing528.com)
(https://www.xing528.com)
若推理句是一个恒真的判断句,则称它是一个定理,显然有
![]()
所谓演绎推理的三段论法可以表示为
![]()
而用集合描述有
![]()
图7.8.7为三段论集合描述的示意图。

图7.8.7 三段论集合
若(A)→(B)是定理,(B)→(C)是定理,则(A)→(C)是定理,这一规则,称为复合原则。用集合表示的复合原则为
![]()
2.模糊蕴涵关系(模糊推理句)
当A、B是模糊集合时,上述推理句就称为模糊推理句。模糊推理句的真值可以根据普通推理句的真值公式来定义。
![]()
“若x是晴天,则x很暖和”的模糊推理句的隶属函数曲线如图7.8.8所示,其中![]() 表示“晴天”的隶属函数,
表示“晴天”的隶属函数,![]() 表示“暖和”的隶属函数,则
表示“暖和”的隶属函数,则![]() 由图中上半部V形实线所描述,它给出了“若晴则暖”为真的程度的定量表示。
由图中上半部V形实线所描述,它给出了“若晴则暖”为真的程度的定量表示。

图7.8.8 ![]()



在上述各式中,R是A→B蕴涵关系。通常使用最多的是1)和2)两种合成运算方法,原因是这两种方法的计算比较简单。
模糊推理过程,可以看成是一个模糊变换器的工作过程。当输入一个模糊子集A',经过模糊变换器R=A→B时,输出为A'◦(A→B),如图7.8.9所示。

图7.8.9 模糊变换器
例7.8.4 若A→B采用积运算式(7.8.15),合成运算“◦”采用最大-最小合成法,式(7.8.23)给定小前提,分别是A'=非常
 ,求广义正向式模糊推理及广义反向式模糊推理的结论。
,求广义正向式模糊推理及广义反向式模糊推理的结论。


当然,此例也可以用不同的蕴涵关系式和不同的合成运算方法来求解。计算后可以发现,有的结论符合实际思维逻辑,有的则不符合。可见,关于模糊推理的理论问题的研究,现在还不成熟。
4.复合模糊条件语句的模糊推理
在模糊推理中,大前提可能不是单一的模糊条件语句,可能是若干条件语句,中间再用一些连接词,如“否则”(else),“与”(and)等连接起来。这类问题的模糊推理称为复合模糊条件语句的模糊推理,分以下几种情况来讨论。



求结论时,蕴涵运算“→”及合成运算“◦”的意义同前。
4)复杂的连接词
大前提中的语句代表着模糊关系,有时实际情况很复杂,可能在多重语句中,还同时使用了连接词“and”“else”“or”和“also”。此时,求解问题的关键是正确地决定大前提的总的模糊蕴涵关系R总。
(1)例如,若大前提的语句为“若x是A则y是B则z是C else z是D”,则R为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




