模糊逻辑的二值与模糊命题

1.命题与逻辑符号

定义7.8.1　一个有意义的陈述句称为命题。如：

（1）该书是用中文写的。

（2）4加2等于6。

（3）他很年轻。

（4）今天气温较高。

定义7.8.2　若陈述句的意义明确，可以分辨真假，这种命题就称为二值命题（简称命题）。

如上述（1）、（2）句。若陈述句的意义是模糊概念，不能用简单的真假分辨，则这种命题就称为模糊命题，如上述（3）、（4）句。

定义7.8.3　对于二值命题，可以用一些连接词如“或”“与”“非”“如果……，那么……”（“若……，则……”）等连接起来。

（1）“或”（or）：用符号“∨”表示，与集合中的并“∪”相对应，又称“析取”，即两个命题至少有一个成立。

（2）“与”（and）：用符号“∧”表示，与集合中的交“∩”相对应，又称“合取”，即两个命题必须同时成立。

（3）“非”（not）：在原命题上加“-”横线，或在命题前加符号，也称否定，它与集合中的补集相对应。

设有如下两个命题。

P：他爱好英语。

Q：他爱好日语。则有P∨Q：表示他爱好英语或爱好日语。

P∧Q：表示他爱好英语和日语。

或P：表示他不爱好英语。

（4）“如果……，那么……”（if…than…）：用符号“→”（或“⇒”）表示，是推断的意思，又称蕴涵，与集合中的包含于“⊂”相对应。例如，如果△ABC是等边三角形（S），那△ABC是等腰三角形（T），用符号写就是：S→T或S⇒T。

（5）“当且仅当”：用符号“↔”（或“⇔”）表示，它表示两个命题等价。

定义7.8.4　一个命题的真与假，叫做它的真值，真常用“1”表示，假常用“0表示。两个命题构成一个复合命题时，它的真值表如表7.8.1所示。

表7.8.1　复合命题的真值表

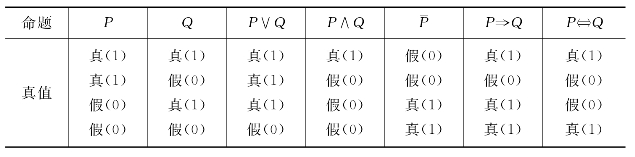
2.模糊命题的真值

模糊命题的取值不是单纯的真和假，但是它反映了真或假的程度。依照模糊集合中隶属函数的形式，模糊命题的真值推广到［0，1］区间上取连续值。

表7.8.2　复合模糊逻辑命题的真值表

由表可知，二值命题的复合运算是模糊命题的复合运算的特例。

模糊命题的“→”（或“⇒”）运算，就是模糊推理，将在以后讨论。

3.格、布尔代数与De-Morgan代数

定义7.8.7（格的定义）　一个集合L，若在其中定义了“∨”与“∧”两种运算，且具有下述性质。

（1）幂等律：若∀α∈L，则有α∨α=α，α∧α=α。

（2）交换律：若∀α，β∈L，则有α∨β=β∨α，α∧β=β∧α。

（3）结合律：若∀α，β，γ∈L，则有

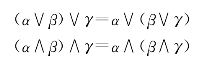
（4）吸收律：若∀α，β∈L，并有

则称L是一个格，并记为L=（L，∧，∨）。（

5）分配律：

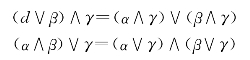
若格L还满足分配律，则称（L，∧，∨）是一个分配格。

定义7.8.8（布尔代数的定义）　除上述性质（1）～（5）外还有

（6）两极律：在L中存在两个元素，记为0和1，如果∀α∈L，则有

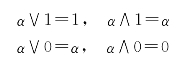
0和1分别称为最小元和最大元。

在L中进一步规定一种一元运算“C”（称为补运算），且满足(www.xing528.com)

（7）复原律：若∀α∈L，则有（αC）C=α。

（8）互补律：α∨αC=1，α∧αC=0。则称（L，∨，∧，C）是一个布尔代数。

例如，（｛0，1｝，∨，∧，C）是一个布尔代数，其中运算：α∨β=max（α，β），α∧β=min（α，β），αC=1-α。

定义7.8.9（De-Morgan代数的定义）　除上述性质（1）～（7）外，还满足De-Morgan律

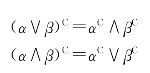
的代数系统称为De-Morgan代数。

De-Morgan代数与布尔代数的显著区别在于前者不满足互补律，即在De-Morgan代数中，一般有

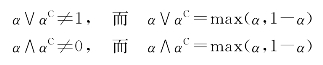
正因为这一点，它才成为研究模逻辑运算的有力工具。

例如，（［0，1］，∨，∧，C）是一个De-Morgan代数，而不是一个布尔代数，因为互补律不成立。若取0.8∈［0，1］，则有

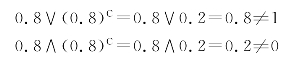
（9）归约律：由二值逻辑的真值表可以证明：“→”及“↔”两种逻辑运算是非独立的，即存在下述等式

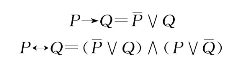
所以在二值逻辑中，独立的逻辑连接词只有三个：“∨”“∧”“—”。

4.模糊逻辑函数

定义7.8.10　若一个逻辑命题的取值是可以变化的，则称这样的逻辑命题为逻辑变量x。

二值逻辑变量的取值是｛0，1｝，而模糊逻辑变量的取值为［0，1］。

定义7.8.11　由逻辑变量x及逻辑运算∨、∧、-和括号所形成的函数F称为逻辑函数（又称逻辑公式）。若变量x的取值及逻辑运算是二值的，则称F是二值逻辑函数（逻辑公式）；若变量x的取值及逻辑运算是模糊的，则称F是模糊逻辑函数（逻辑公式）。

表7.8.3　

6.模糊逻辑函数的范式

定义7.8.12（析取范式）　若xij是逻辑变量，则下列逻辑函数称为析取范式（逻辑并标准形）：

定义7.8.13（合取范式）　若xij是逻辑变量，则下列逻辑函数称为合取范式（逻辑交标准形）：

式中：∑表示连加，即…∨…∨…∨…；表示连乘，即…∧…∧…∧…。所以析取标准型为“积之和”型，而合取标准型为“和之积”型。

一般地，对于一个给定的模糊逻辑函数式，总可以通过等价变换使其成为析取范式或合取范式，或是析取范式和合取范式的组合。

为了把模糊逻辑函数式化成标准型，我们要利用以下两个定理（因证明要占很大篇幅，故略去证明）。

定理7.8.1　公式F在模糊逻辑中为真，当且仅当该公式在二值逻辑中为真（定义：当模糊逻辑公式F的取值大于等于时，称F为真）。

定理7.8.2　公式F在模糊逻辑中可化成标准型，当且仅当F在二值逻辑中可化成标准型。

以下举例说明模糊逻辑函数化成标准型的方法。

例7.8.1　设x、y、z均为模糊逻辑变量，它们分别为某些命题的真值，试求模糊逻辑函数

的析取范式和合取范式。

先求析取范式。为此先确定逻辑变量x、y、z分别为0和1时的模糊逻辑函数值（相当于二值逻辑的情况），结果如表7.8.4所示。

表7.8.4　二值逻辑真值表

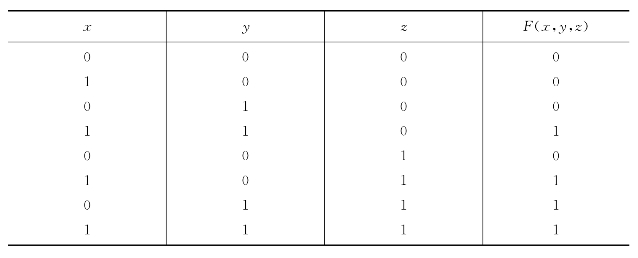
用逻辑函数F（x，y，z）=1时所对应取1的逻辑变量求交作为析取范式的一项，例如表中第四行，F（x，y，z）等于1，对应x=1，y=1，故x∧y即析取范式的一项。最后对析取范式的每一项求并，再根据吸收律化简，即可求得析取范式为

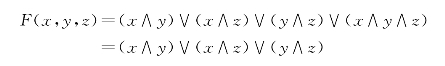
求合取范式的步骤与上式类同，只不过按F（x，y，z）=0时取值为0的逻辑变量求并作为合取范式的一项，然后对各项求交后再化简，所得的合取范式为

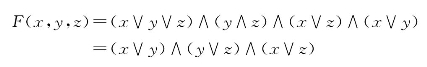
由以上求得的析取范式与合取范式不难看出，对于同一模糊逻辑函数，两种范式之间是对偶的。

如果逻辑函数式中的逻辑变量有的形式，则通过真值表示范式时，选取每一子项应遍历所有变量。例如求析取范式时，根据F（x，y，z）=1的那一行，应取1的变量和取0的变量的补。表7.8.4中第四行，当F（x，y，z）=1时，x=1，y=1，z=0，故应选x∧y∧为析取范式的一项。当然，在例7.8.1中选取每一子项时，也可遍历所有变量，化简后其结果是相同的。

关于化简模糊逻辑函数的问题（极小化问题），限于篇幅在此不进一步讨论了。