多层次模糊综合评判技术优化

当评判问题中考虑的因素很多时，一方面是较难决定权重系数，另一方面，由于要满足“归一化”（即）的要求，使每一因素分得的权重系数值很小，不易分出主要因素。加上在合成运算中，取大（∨）、取小（∧）这两个运算往往会丢失许多有价值的信息，导致最后评判的结果分辨率很差，甚至得不到评判结果。

为此，在因素众多时，常采用分层法来解决上述问题。分层法的要点就是将因素按某些属性分成几类。例如，在高等学校之间评比，可以就校风校貌、教学、科研等几个方面进行考虑，在它们之间确定权重分配，于是可以进行综合评判。而这里的每一方面的单因素评价，又是低一层次的多因素综合的结果。如“教学”的好坏是“师资，教学设施，学生能力”等因素的综合。同样，低一层次的单因素评价（如师资的优劣），也可以是更低一层次的多因素的综合。由此，我们设计出多因素模糊综合评判模型。

多层次模糊综合评判的步骤如下：

（1）将因素集X=｛x1，x2，…，xn｝按某些属性分成s个子集

满足条件：

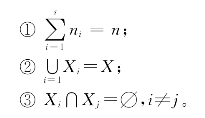
（2）对每一子因素Xi，分别作出综合决策，设Y=｛y1，y2，…，ym｝为评价集，Xi中的各因素的权重分配为(www.xing528.com)

图7.7.3　二级评判模型

若一级因素集Xi（i=1，2，…，s）仍含有较多的因素，还可将Xi再分小，于是有三级模型、四级模型，等等。

例7.7.4　评价一批产品质量，因素集有九项指标，X=｛x1，x2，…，x9｝。评价分为四等：y1=一等品，y2=二等品，y3=次品，y4=废品，于是Y=｛y1，y2，y3，y4｝。评判小组由专家、检验人员、用户组成，他们分别从不同的着眼点进行评价，分别得出单因素评判矩阵