解析不完全评判问题

在综合评判中，有4个基本要素：（

1）因素集X=｛x1，x2，…，xn｝；

（2）评价集Y=｛y1，y2，…，ym｝；

（3）单因素评判矩阵=（rij）n×m；

（4）各因素的权重分配

由于实际问题的复杂性，有时评价因素很难搞清楚，此时就缺少一个基本要素——因素集。这类评判问题，称为不完全评判问题。对于这类问题，首先要构造一个因素集，使得不完全评判问题“完全化”。

实践表明，对于那些可观察，可划分、可比较的因素，可以用下列方法将因素集X和权重分配同时构造出来。

第一步，构造因素集X。

（1）将X等分为m1份，按某种原则α，取出其中一份，记为x1，它与总体X的比为k1；

（2）将X等分为m2份（m2＜m1），按既定原则α，取出其中一份，记为x2，它与X的比为k2；

⋮

（n-1）将X等分为m n-1份（mn-1＜mn-2），按原则α，取出其中一份，记为xn-1，它与X的比为kn-1；

（n）取xn=X，显然它与X的比为k n=1。

于是得到因素集X=｛x1，x2，…，xn｝。

第二步，构造权重分配。

令

则=（a1，a2，…，an）便是诸因素的权重分配。

易知，此时构造的因素集是某种类别因素，例如第1类，第2类，……很难说出这个因素是什么，因此权重系数也仅说明某类的权重是多少，当然最后一类的权重就较大。但在作单因素评价矩阵时，相应的就应按每类作出评价，而后加以综合。

例7.7.3　对中成药糖衣片的“花片”严重程度作评判。(www.xing528.com)

中成药糖衣不均匀的药片俗称“花片”，严重者是不允许出厂的。花片的程度通常分为四等：

这样，就有决策集Y=｛y1，y2，y3，y4｝。

然而，影响花片的原因很复杂，故因素集是未知的，因而这是一个不完全的评判问题。

假定生产了一批糖衣药片，随机抽取100片，对其中每一片都做下列的分划（是面积的划分，而非实体割开），如图7.7.2所示。在分划后的子体中，选取原则α定为选择花色程度严重者。

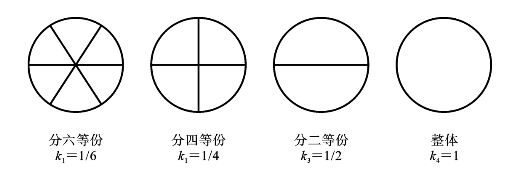
图7.7.2　剖分图

先对1/6子体x1作单因素决策。在100片药片中，若有10片定为极花，15片定为较花，20片定为轻花，55片定为不花，则得出关于x1的单因素评判向量

（0.1，0.15，0.2，0.55）

类似地，对1/4子体x2、1/2子体x3、整体x4如此处理，也得出相应的单因素评判向量

（0，0.1，0.3，0.6）

（0，0，0.2，0.8）

（0，0，0.15，0.85）

由此构造出单因素评判矩阵：

另外，由式（7.7.6）计算出权重分配为

由此立刻算出，综合评判向量

因此这批药片定为不花，可以出厂。