经典关系只能说明元素之间关系的有无。现实世界的关系不是简单的有无,而是有不同程度的相关性质。例如家庭成员之间相貌相似的关系,就不是简单的相似或不相似,而是有不同的相似程度。反映这种性质的关系就是模糊关系。
定义7.6.7 设X、Y为两个论域,在X×Y上的任何一个模糊集![]() ∈F(X×Y)都称为X与Y之间的模糊关系,即
∈F(X×Y)都称为X与Y之间的模糊关系,即
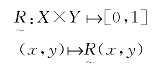
其中![]() 称为x与y关于
称为x与y关于![]() 的关系强度。当X=Y时,称
的关系强度。当X=Y时,称![]() 为X上的模糊关系。
为X上的模糊关系。
例7.6.5 医学上常用
体重(kg)=身高(cm)-100
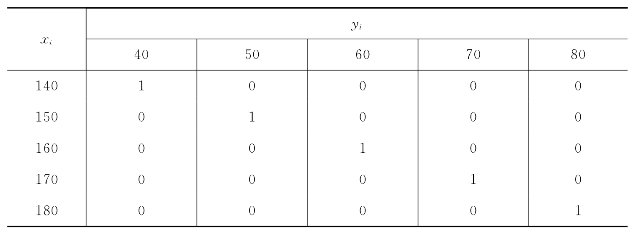
描述标准体重,这实际上给出了身高(论域X)与体重(论域Y)的普通关系。若X={140,150,160,170,180},Y={40,50,60,70,80},则普通关系由表7.6.2给出。它的关系矩阵是个布尔矩阵

表7.6.2 体重与身高的普通关系R(xi,yj)
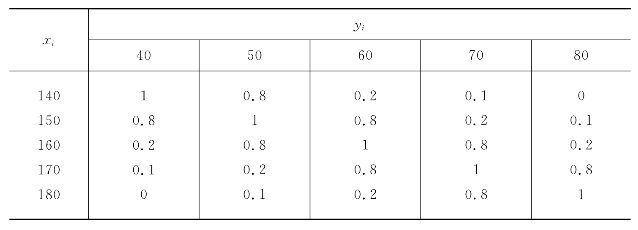
人有胖瘦不同,所以大部分人并非严格的标准情况,而是与标准情况有不同的接近程度,显然这更能完整、全面地描述身高与体重的关系,如表7.6.3所示。
表7.6.3 体重与身高的模糊关系
当![]() ;
;
当![]() ,这说明身高170 cm与体重60 kg的人与标准情况接近的程度为0.8,或其关系强度为0.8;身高180 cm与体重50 kg的人与标准情况接近的程度为0.1,或其关系强度为0.1。
,这说明身高170 cm与体重60 kg的人与标准情况接近的程度为0.8,或其关系强度为0.8;身高180 cm与体重50 kg的人与标准情况接近的程度为0.1,或其关系强度为0.1。
这个模糊关系的矩阵形式如下:

一般地,对于有限论域![]() 之间的模糊关系
之间的模糊关系![]() 可用n行m列(简称n×m阶)的模糊矩阵来表示:
可用n行m列(简称n×m阶)的模糊矩阵来表示:
![]()
其中![]() 。
。
例7.6.6 设有一组学生X={甲、乙、丙},他们可以选学Y={英、法、德、日}中的任意几门外语,他们的结业成绩见表7.6.4。(https://www.xing528.com)
表7.6.4 外语成绩表

若把他们的分数除以100,则得X与Y之间的一个模糊关系![]() ,见表7.6.5。
,见表7.6.5。
表7.6.5 模糊关系表
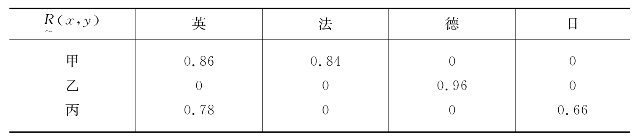
它的矩阵形式为

有限论域上的模糊关系除了可以用矩阵表示外,还可以用模糊关系图来表示,如图7.6.4所示。
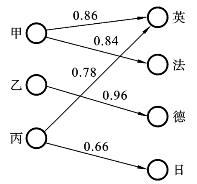
图7.6.4 模糊关系图
由于模糊关系是一种特殊的模糊集,即X×Y上的模糊集,故其运算与模糊集的运算完全一致,即包含关系,恒等关系,并、交、补的运算都有相同的定义;模糊关系的运算符合幂等、交换、结合、吸收、分配、两极、复原、对偶等规律,但不符合排中律![]() 的λ截集
的λ截集![]() 是X与Y之间的普通关系,前述的截集的性质也完全适用于截关系。
是X与Y之间的普通关系,前述的截集的性质也完全适用于截关系。
记

它们分别称为零矩阵、单位矩阵和全矩阵。
![]() 的截关系Rλ称为λ截矩阵,记为
的截关系Rλ称为λ截矩阵,记为

其中



免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




