经典映射关系及其表达方式

“关系”是一个普通使用的，很重要的概念。例如父子关系、兄弟关系、朋友关系、大小关系、从属关系、买卖关系、供求关系、合作关系等，它表示了事物之间的某种联系。在数学上，关系有严格的定义。

定义7.6.1　设X、Y为两个非空集合。X×Y为X与Y的笛氏积，即X×Y=｛（x，y）|x∈X，y∈Y｝。若有R⊂X×Y（即），则称R为X到Y的二元关系，简称关系。对于任何一个（x，y）∈X×Y，若（x，y）∈R，则称x与y具有关系R，记作xRy；若（x，y）∉R，则称x与y不具有关系R，记作xRy。

若X=Y，R是从X到Y的关系，则可称R是X上的关系。

例7.6.1　设X、Y是实数集，R是X上的“大于”关系，即

则R是坐标平面上直线y=x（不含直线上的点）那部分平面的点集（见图7.6.1）。

图7.6.1　关系是映射

若X与Y之间有一规则R，使得∀x∈X，按规则R唯一地与y∈Y，则R决定了X到Y的映射

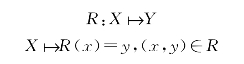
由此可见，映射中的规则R，就是关系R。

从X到Y的关系R是论域X×Y的经典子集。所以经典集的并、交、补运算及其性质，以及经典集的特征函数表示法，对R当然适用。

例7.6.2　设有四个学生甲、乙、丙、丁，用优、良、差来衡量他们的学习成绩。若作出两个集合

再作其直积（笛氏积）

如果已知甲的成绩是优，乙和丙的成绩是良，丁的成绩是差，则

就是X与Y之间的一个关系，即R⊂X×Y，它表示了甲、乙、丙、丁四个学生与其成绩的对应关系，所以这个关系也是一个映射，如图7.6.2所示。

图7.6.2　关系也是映射

关系也可以用表格表示（见表7.6.1）。

表7.6.1　学习成绩关系表

表中“1”表示（x，y）∈R，“0”表示（x，y）∉R。如（甲，优）∈R，则在相应的位置上写上“1”；（甲，优）∉R，则在相应的位置上写上“0”。表7.6.1形式上可以简洁地用矩阵形式写出：

称为关系矩阵。它的一般形式为

经典关系可用特征函数来表示。

定义7.6.2　若，则其特征函数表示如下：

当，则二元关系R的特征函数组成一个布尔矩阵（矩阵中的元素或者为0，或者为1），如式（7.6.1）所示。但其中的元素rij选取如下：

(www.xing528.com)

定义7.6.3　设R是X到Y的关系，令

则R-1是Y到X的关系，称R-1为R的逆关系。

定义7.6.4　设R是Y到X的关系，Q是Y到Z的关系，令

则R◦Q是X到Z的关系，称为R到Q的合成（或复合）关系（参见图7.6.3）。

图7.6.3　合成关系R◦Q

若用特征函数来表示合成运算，则有

使

因而有

例7.6.3　图7.6.3所示之例，用特征矩阵写出有

从图7.6.3可以直接看出

由式（7.6.4）可以计算出R◦Q（x，z）。这里和普通矩阵的运算类似，只要用“∧”代替“×”，用“∨”代替“+”即可。易知，计算结果与直接观察的结果是相同的。

定义7.6.5　设R是X上的经典关系，则有如下定义：

称R是自反的⇔∀x∈X，（x，x）∈R；

称R是对称的⇔若（x，y）∈R，则（y，x）∈R；

称R是传递的⇔若（x，y）∈R，（y，z）∈R，则（x，z）∈R；

称R是X上的等价关系⇔R是X上的一个自反、对称和传递的关系。

若R是X上的等价关系，∀x∈X，称

为以x为代表的模R的等价类；称

为以X的模R的商集，X/R是集合的集合。

例7.6.4　设X为整数集，令