经典集合论的基本概念解析

1.集合运算

由于经典集合论是经典数学的基础，同时了解模糊集合论又必须与经典集合论相对照，为了能循序渐进地学习模糊集合论，有必要先将经典集合论中的一些与模糊集合论有关的基本概念先给予介绍。

定义7.1.1　论域是所论数学对象的全体。它可以是无穷集，例如自然数的全体。但它不能是“不以自己为元素的集合”的全体，即不能是“非本身分子集”的集合。这样就避免了Russell悖论的情况。事实上，我们研究某问题时，并不关心那些与所论问题无关的对象。

定义7.1.2　设X是论域，A是X的子集，即A的所有元素均是X的元素，或者说A是X中某些元素组成的集。

x是A的元素（或x属于A），记为x∈A，x不是A的元素（或x不属于A），记为x∉A。在经典集合论范围内，对任一元素x而言，或者x∈A，或者x∉A，二者必居其一。

以上并、交、补、差集的定义及对偶律可以用图7.1.1来形象地表示。

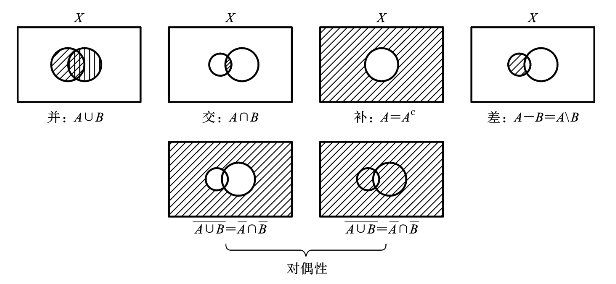
图7.1.1　并、交、补、差集的定义及对偶律

分配律与对偶律有以下更一般的形式：设T为某指标集，有

（4＇）分配律：

（9＇）对偶率：

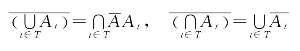
以上各命题的证明是显然的，故从略。

2.映射

定义7.1.9　设A、B是两个集合，若有一规则f，使每一个x∈A唯一确定一个y∈B与之对应，则称f是从A到B的一个映射，记为

f∶A→B

A称为映射f的定义域，B称为f的值域；y称为在x作用下的象，记作y=f（x），并用符号

表示，x称为y的一个原象。

由此可见，一个映射必须联系两个集合（可以是同一论域上的集合，也可以不是同一论域上的集合）和一个对应规则。(www.xing528.com)

例7.1.1　取A=［0，2π］，B=［-1，1］，从A到B的映射：

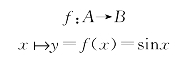
是我们熟知的正弦函数。

通常我们了解的函数都是映射，因此函数是映射的特殊形式。在现代数学中，映射与函数是同义词。

定义7.1.10　设A=B，映射

图7.1.2　集合的映射与逆映射

这是A的一个子集，叫做在f作用下T的完全原象。f-1（T）又称为f的逆映射。显然，一个映射若可逆，则其逆映射是唯一的。

定义7.1.12　设A、B、C是三个集合，已知两个映射为f∶A→B，g∶B→C，则可以确定一个A到C的映射

称为映射f与g的合成映射（或复合映射），记为h=g◦f。

例7.1.3　设，已知映射f和g分别为

则它们的合成映射h=g◦f为

因为f不是单射，g也不是单射，所以f和g都不可逆，合成映射h当然也不可逆。

3.特征函数

定义7.1.13　称下述映射

中的函数μA（x）为X上集合A的特征函数，其值为