解密中国邮递员的路线问题

中国邮递员问题是由我国学者管梅谷于1962年首先提出的。邮递员负责某一片区邮件的投递与收取工作，每天他从邮局出发，沿街道去收集和投递邮件，然后回到邮局。他期望把所有的街道只走一遍回到邮局，但有时必须重复走一些街道才能实现。问题是重复走哪些街道才是最省的？用图的语言描述就是：在一个连通图中，每条边上赋予一个非负的权w（eij），要求一个圈（未必是简单图），使得过每条边至少一次，并使圈的总权最小。

可以发现，中国邮递员问题本质上是一笔画问题。一笔画问题与本章开始所讲的“哥尼斯堡的七座桥”问题有类似之处。给定一个连通多重图G，若存在一条链，过每条边一次而且仅一次，则称这条链为欧拉链。若存在一个简单圈，则称这个圈为欧拉圈。一个图若有欧拉圈，则称之为欧拉图。显然一个图，若能一笔画成，则这个图必是欧拉圈或含有欧拉链。

关于一笔画问题，有如下的性质：

定理6.6.1　连通多重图G是欧拉图，当且仅当G中无奇点。

定理6.6.2　连通多重图G有欧拉链，当且仅当G中恰有两个奇点。

上述定理提供了判断一个图是否能够一笔画成的依据，同时也为求解中国邮递员问题提供了思路。根据上述性质，如果邮递员所负责的区域图中没有奇点，他就可以从邮局出发，经过每一条街道仅一次回到邮局，这样所走的路程也是最短的。对于有奇点的图，就必须重复走一些街道才能回到出发点。所以，中国邮递员问题可以描述为：在一个包含奇点的连通图中，增加一些重复边使得该图中不再包含奇点，同时要求增加的重复边的总权最小。

求解中国邮递员问题的方法称为奇偶点图上作业法，其基本步骤如下。

（1）初始可行方案的确定：配对图中所有奇点（因为图中的奇点总是偶数个），确定每对奇点之间的一条链（连通图任意两点之间至少有一条链），然后在这条链上所有的边都加重复边。这样可以使得图不再包含奇点。

（2）可行方案的调整：最优方案应满足如下条件。

①在最优方案中，图的每一条边上最多有一条重复边。如果某条边存在着多条重复边，应去掉偶数条边，使得该边最多有一条重复边。

②在最优方案中，图中每个圈上的重复边的总权不应大于该圈总权的一半。如果存在重复边的总权大于该圈总权的一半，则应将现有的重复边去掉，而在没有重复边上加重复边。

当上述两个条件都得到满足时，就得到了中国邮递员问题的最优解了。

例6.6.1（中国邮递员问题）　求解如图6.6.1所示的中国邮递员问题，边旁的数字为两点间的距离。(www.xing528.com)

图6.6.1

解　（1）确定图中的奇点，包括v2，v4，v5，v6，v7，v8，v9，v11共8个。配对这些奇点，如（v2，v11），（v4，v7），（v5，v8），（v6，v9）组成4对。

（2）在每对奇点间确定一条链，并对该链中的边都加上一条重复边。假设4对奇点之间的链分别为（v2，v11）：v2→v1→v4→v7→v10→v11；（v4，v7）：v4→v7；（v5，v8）：v5→v6→v9→v8；（v6，v9）：v6→v9。每条链上加重复边后得到图6.6.2。

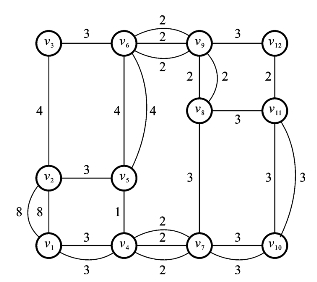
图6.6.2

（3）删除边（v4，v7）和（v6，v9）上多余的重复边，得到图6.6.3，此时重复边的总权为23。

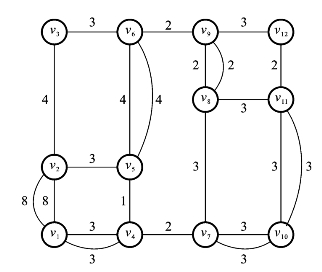
图6.6.3

（4）在圈v1→v2→v5→v4→v1中，重复边的总权为8+3=11，大于该圈总权的一半7.5，所以将（v1，v2）和（v1，v4）的重复边去掉，在（v2，v5）和（v4，v5）上加上重复边得到图6.6.4所示的结果。此时重复边的总权为16，减少了7。

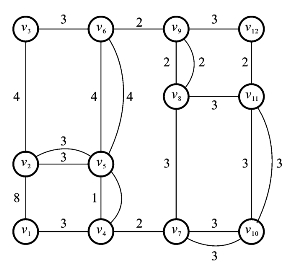
图6.6.4

（5）在所有的圈中都不存在重复边的总权大于该圈总权一半的情况，所以图6.6.4为该问题的最优解。