最小费用最大流问题的优化求解

前述网络最大流问题中，只考虑每条弧上的容量限制。在实际问题中，除了容量限制外，还要考虑每条弧上单位流量的费用。给定网络D=（V，A，C），对于每条弧（vi，vj）∈A上除了已给容量c ij外，还要给定一个单位流量的费用b（vi，vj）≥0（简记为bij），所谓最小费用最大流问题就是要求一个最大流f，使得流的总费用达到最小值。

从前面的网络最大流的求法中可以发现，当网络达到最大流时，流量在弧集合上的分布可能不同，这样使得同样的最大流量可能得到的流量费用也就不同，最小费用最大流就是要求当网络流量达到最大时费用最小的流量分布。所以最小费用最大流问题可以分解为两个步骤：首先确定网络的最大流量，然后调整弧集合流量的分布，以使得网络的费用最小。但在实际求解时，通常将上述两个过程整合到一起来进行。我们知道，确定网络的最小费用可以使用前面的最短路的求法，而最大流求法是在增广链上增加流量。只要保证根据费用确定网络中从vs到vt的最短路是增广链，这样在最短路增加流量所带来的费用增加是最少的（因为流量与费用都是非负的）。但是，如何保证从vs到vt的最短路总是增广链呢？增广链的要求是前向弧流量小于容量，后向弧的流量非负，所以当前向弧的流量等于容量或后向弧的流量为零时都不应该出现在最短路中。

为了实现上述要求，首先设网络的初始流量为零。然后将网络中的弧都转化为双向的弧，其费用权按如下方式确定：

按此方式可以构造一个关于网络费用的赋权有向图w（f），其前向弧的流量均小于容量，后向弧的流量均不为0，在该图中寻找从vs到vt的最短路，如果存在，则它必为一条增广链。然后在该增广链上按标号法调整网络流量，具体调整方法为

其中，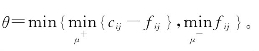

按此方法即可增加网络流量，且增加的费用最少。若不存在从vs到vt的最短路，则表明网络已经达到最大流量，当前流量即最小费用最大流。

例6.5.1（最小费用最大流）　求图6.5.1所示网络的最小费用最大流，弧旁数字为（bij，cij）。

图6.5.1

解　（1）取f0=0，为初始可行流。

（2）构造赋权有向图w（f（0）），并求得从vs到vt的最短路vs→v2→vt，如图6.5.2所示。

(www.xing528.com)

图6.5.2　w（f（0））

（3）在原网络中确定该增广链的流量为1，得到f（1），如图6.5.3所示。

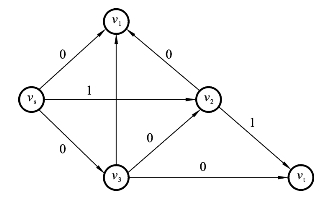
图6.5.3　f（1），v（f（1））=1

（4）根据f（1）作赋权有向图w（f（1）），并求得从vs到vt的最短路vs→v3→vt，如图6.5.4所示。

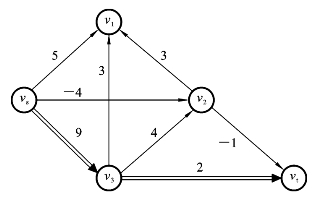
图6.5.4　w（f（1））

（5）在原网络中确定该增广链的流量调整量为2，得到f（2），如图6.5.5所示。

图6.5.5　f（2），v（f（2））=3

（6）根据f（2）作赋权有向图w（f（2）），如图6.5.6所示，该网络不存在从vs到vt的最短路，所以得到网络的最小费用最大流为f（2），总费用为27。

图6.5.6　w（f（2））