Dijkstra标号法优化路径搜索

1.基本方法

最短路问题是网络分析与优化中的一个基本问题，它不仅可以直接应用于解决生产实际的许多问题，如管道铺设、线路安排、厂区布局等，而且经常被作为一个基本工具，用于解决其他的优化问题。

定义6.3.1　给定一个赋权有向图D=（V，A），记D中每一条弧aij=（vi，vj）上的权w（aij）=wij，又给定D中的一个起点vs和终点vt，设P是D中从vs到vt的一条路，则定义路P的权是D中所有弧的权之和，记为W（P），即

又若P*是图D中从vs到vt的一条路，且满足

式中，对D的所有从vs到vt的路P取最小，则称P*为从vs到vt的最短路，W（P*）为从vs到vt的最短距离。

在一个图D=（V，A）中，求从vs到vt的最短路和最短距离的问题就称为最短路问题。

定理6.3.1　设P是D中从vs到vj的最短路，vi是P中的一点，则从vs沿P到vi的路也是从vs到vi的最短路。

证明　可用反证法证明。设此结论不成立，设Q是从vs到vi的最短路，令P＇是从vs沿Q到达vi，再从vi沿P到达vj的路，则P＇的权就比P的权小，这与P是从vs到vj的最短路矛盾。

求解最短路问题，目前公认最好的方法是由Dijkstra于1959年提出的标号法，它适用于所有的wij≥0的情形。该方法的主要特点是以起始点vs为中心向外层层扩展，直到扩展到终点vt为止。每次扩展，都向外探寻最短路，执行过程中，给每一个顶点vj标号为

（λj，lj）

其中，λj是正整数，它表示获得此标号的前一点的下标；lj或表示从起点vs到该点vj的最短路的权（称为固定标号，记为P标号），或表示从起点vs到该点vj的最短路的权的上界（称为临时标号，记为T标号）。事实上，网络中的点被划分为P和T两个集合。方法的每一步都去修改T标号，并且把某一个具有T标号的点改变为具有P标号的点，从而使D中具有P标号的顶点数多一个，这样至多经过n-1步就可以求出vs到各点的最短路。

以下举例说明如何根据定理6.3.1应用Dijkstra标号法求解最短路问题，然后再归纳出Dijkstra标号法的计算步骤。

例6.3.1　图6.3.1所示为某地区的交通运输示意图，试问：从v1出发，经哪条路线到达v8才能使总行程最短？用Dijkstra标号法求解。

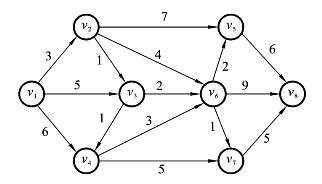
图6.3.1

解　开始时，令i=0，s=1，S0=｛v1｝，λl=0，P（v1）=0，T（vj）=+∞，λj=1（j=2，3，…，8），k=1，即给起点v1标（0，0），给其余的点标（1，+∞），这时v1为获得P标号的点，其余为T标号的点。

考察与v1相邻的点v2，v3，v4（见图6.3.2）。

图6.3.2

因（v1，v2）∈A，v2∉S0，故把v2的临时标号修改为

T（v2）=min｛T（v2），P（v1）+w12｝=min（+∞，0+3）=3

这时λ2=1，同理可得

T（v3）=min｛+∞，0+5｝=5，　λ3=1

T（v4）=min｛+∞，0+6｝=6，　λ4=1

其余点的T标号不变。

在所有的T标号中，最小的T（v2）=3，于是令P（v2）=3，S1=S0｛v2｝=｛v1，v2｝，k=2。

i=1：

这时v2为刚获得P标号的点，考察与v2相邻的点v5，v6，v3（见图6.3.3）。

图6.3.3

因（v2，v5）∈A，v5∉S1，故把v5的临时标号修改为

T（v5）=min｛T（v5），P（v2）+w25｝=min｛+∞，3+7｝=10

这时λ5=2，同理可得

在所有的T标号中，最小的T（v3）=4，于是令P（v3）=4，S2=S1∪｛v3｝=｛v1，v2，v3｝，k=3。

i=2：

这时v3为刚获得P标号的点，考察与v3相邻的点v4，v6（见图6.3.4）。

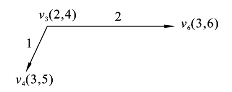
图6.3.4

因（v3，v4）∈A，v4∉S2，故把v4的临时标修改为

T（v4）=min｛T（v4），P（v3）+w34｝=min｛6，4+1｝=5，　λ4=3

同理可得

T（v6）=min｛7，4+2｝=6，　λ6=3

在所有的T标号中，最小的T（v4）=5，于是令P（v4）=5，S3=S2∪｛v4｝=｛v1，v2，v3，v4｝，k=4。

i=3：

这时v4为刚获得P标号的点，考察与v4相邻的点v6，v7（见图6.3.5）。

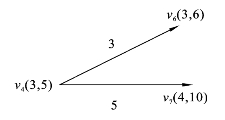
图6.3.5

因为（v4，v6）∈A，v6∉S3，故把v6的临时标号修改为

T（v6）=min｛T（v6），P（v4）+w46｝=min｛6，5+5｝=6

这时v6的临时标号不修改，故λ6=3，同理可得

T（v7）=min｛+∞，5+5｝=10，　λ7=4

在所有的临时标号中，最小的为T（v6）=6，于是P（v6）=6，S4=S3∪｛v6｝=｛v1，v2，v3，v4，v6｝，k=6。

i=4：

这时v6为刚获得P标号的点，考察与v6相邻的点v5、v7、v8（见图6.3.6）。

图6.3.6

因为（v6，v5）∈A，v5∉S4，故把v5的临时标号修改为

T（v5）=min｛T（v5），P（v6）+w65｝=min｛10，6+2｝=8

这时，λ5=6，同理可得

T（v7）=min｛10，6+1｝=7，　λ7=6

T（v8）=min｛+∞，6+9｝=15，　λ8=6

在所有的临时标号中，最小的为T（v7）=7，于是令P（v7）=7，S5=S4∪｛v7｝=｛v1，v2，v3，v4，v6，v7｝，k=7。

i=5：

这时v7为刚获得P标号的点，考察与v7相邻的点v8（见图6.3.7）。

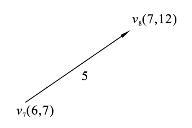
图6.3.7

因为（v7，v8）∈A，v8∉S5，故把v8的临时标号修改为

T（v8）=min｛T（v8），P（v7）+w78｝=min｛15，7+5｝=12

这时λ8=7。

在所有的临时标号中，最小的为T（v5）=8，于是令P｛v5｝=8，S6=S5∪｛v5｝=｛v1，v2，v3，v4，v5，v6，v7｝，k=5。

i=6：

这时v5为刚获得P标号的点，考察与v5相邻的点v8（见6.3.8）。

图6.3.8

因为（v5，v8）∈A，v8∉S6，故把v8的临时标号修改为

这时v8的临时标号不修改，故λ8=7。(www.xing528.com)

最后只剩下v8一个临时标号点，故令

P（v8）=T（v8）=12，　λ8=7

至此，找到从起点v1到终点v8的最短距离为12，再根据第一个标号λj，反向追踪求出最短路径为

v1→v2→v3→v6→v7→v8

事实上，按照这个算法，也找出了从起点v1到各中间点的最短路径和最短距离，例如

v1→v2→v3→v6→v5

就是从v1到v5的最短路径，距离为8。

以下再回过头将Dijkstra标号法的具体步骤汇总如下：

开始时，令算法段i=0，s=1，第一标号集S0=｛v1｝，λ1=0，标号P（v1）=0，对于每一个vj≠vs，令T（vj）=+∞，λj=s，k=s。

（1）如果Si=V，算法终止，这时，对于每个vj∈Si，L j=P（vj）；否则，转下一步。

（2）设vk是刚获得P标号的点，考察每个使（vk，vj）∈A，且vj∉Si的点vj，将T（vj）修改为

如果T（vj）＞P（vk）+wkj，则将T（vj）修改为P（vk）+wkj，将λj修改成k；否则不修改。

（3）令

如果T（vj）＜+∞，则将vj的下标变为P标号，即令P（vj）=T（vj），令Si+1=Si｛vj｝，k=j。

把i换成i+1，返回（1）；否则终止。这时对于每一个vj∈Si，有l（vj）=P（vj）；而对于每一个vj∉Si，有l（vj）=T（vj）。

为了简化计算，还可以采用每次只记录从起点v1到各点的最短距离或上界的方法，为此我们引入记号

表示在第i次标号中各点的距离或上界。例如在例6.3.1.1中，我们也可以按如下方式进行：

L0=（0，∞，∞，…，∞）

于是

有“·”号的点表示P标号点。

最后按后面的轨迹记录反向追踪可求得从起点到终点v8的最短路径，且最后一轮标号L7中所表示的就是从起点v1到各点的最短距离。

2.改进的标号法

另外，本算法在给某个点标号时，也可以通过找该点的各个来源点的方法来实现，具体做法如下：

开始时，给起点vs标（0，0），即λ1=0，l（vs）=0。

一般地，在给点vj标号时，要找出所有与vj有弧相连且箭头指向vj的各点（称为vj的来源点），不妨设vi1，vi2，…，vim是vj的来源点，其标号为l（vi1），l（vi2），…，l（vim）。w（i1，j），w（i2，j），…，w（im，j）为弧（vi1，vj），（vi2，vj），…，（vim，vj）的权重，则给定点vj标以（vk，l（vj）），其中

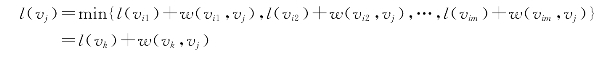
根据定理6.3.1可知，由始点vs到vj的最短路径必是由vs到某个vk的最短路径再加上弧（vs，vj）的权重，vk是v1到vj最短路径上的点，且是vj的来源点，显然，l（vj）是v1到vj最短路径的长度。所以给每个顶点以标号（vk，l（vj）），j=1，2，…，n，即可获得最短路径线路和长度的信息。

下面，以图6.3.1为例，说明改进的标号法的具体过程。

首先给始点v1标号，第一个标号表示的是来源点，第二个标号表示l（v1），由于v1是始点，故令始点的第一个标号为0，令l（v1）=0，于是得到始点v1的标号（0，0）。

v2的来源点是v1，且l（v2）可以由下式计算，即

l（v2）=min｛l（v1）+w（v1，v2）｝=min｛0+3｝=3

于是得到v2的标号（v1，3）。

v3点的来源点v1、v2，计算

于是得到v3的标号（v2，4）。

v4的来源点有v1、v3，计算

于是得到v4的标号（v3，5）。

v5的来源点有v2、v6，计算

于是得到v5的标号（v6，8）。

v6的来源点有v2、v3、v4，但v6还未标号，而v6的来源点都已获得标号，故可计算

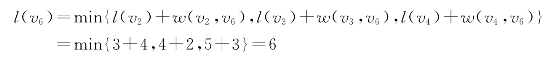
于是得到v6的标号（v3，6）。

v7的来源点是v4、v6，计算

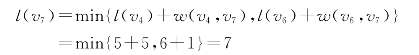
于是得到v7的标号（v6，7）。

最后终点v8的来源点是v5、v6、v7，计算

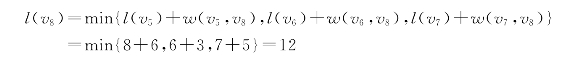
所以在终点v8处标上（v7，12），标号过程结束，如图6.3.9所示。

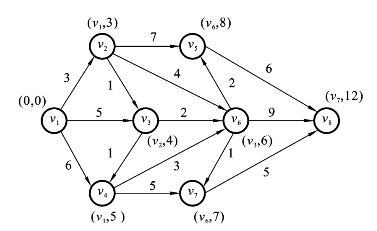
图6.3.9

我们沿第一个标号，由终点反向跟踪，很容易求得该网络的最短路径v1→v2→v3→v6→v7→v8，而终点v8的第二个标号就是此最短路长度。

上述标号过程中，不仅可以求得v1到v8的最短路，而且从v1到vj（j=2，3，4，5，6，7）的最短路也可求得。例如，从v1到v5的最短路径是v1→v2→v3→v6→v5，最短路长度为8。

归纳上述例子，可以总结改进标号法的一般步骤如下：

（1）始点vs标以（0，0）。

（2）考虑需要标号的顶点vj，设vj的来源点vi1，vi2，…，vim均已获得标号，则vj处应标以（vk，l（vj）），其中l（vj）按式（6.3.4）确定。

（3）重复第（2）步，直至终点vj也获得标号为止，l（vj）就是最短路径的长度。

（4）确定最短路径，从网络终点的第一个标号反向跟踪，即得到网络的最短路径。

综上所述，例6.3.1是非负权（即w（vi，vj）≥0）网络最短路径的求解，对于含有负权（即w（vi，vj）＜0）网络的情形，改进的标号法也是适用的。

例6.3.2　求图6.3.10所示从始点v1到各点的最短路径。

图6.3.10

解　采用改进的标号法求解。

首先在始点v1标以（0，0），然后在v3处标以（v1，-2），由于

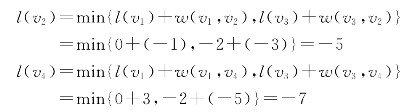
所以在v2和v4处依次标以（v3，-5）和（v3，-7），然后在v6处标以（v3，-1）。

由于

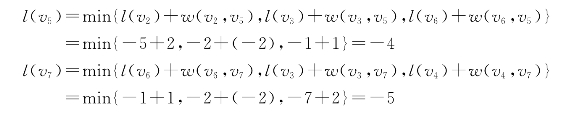
所以在v5和v7处分别标以（v3，-4）和（v4，-5）。

最后由于

所以在终点v8处应标以（v7，3）。

所有点都获得标号，标号结果如图6.3.11所示。反追踪得到v1至v8的最短路径为v1→v3→v4→v7→v8，长度为3。

图6.3.11