支撑树与最小树：全面解析

定义6.2.2　设图G1=（V，E1）是图G=｛V，E｝的支撑子图，如果G1是一棵树，记T=（V，E1），则称T是G的一棵支撑树。

定理6.2.1　图G有支撑树的充分必要条件是图G的连通。

证明　必要性是显然的。

充分性的证明如下：

设G是连通图。

（1）如果不含圈，由定义6.2.1可知，G本身就是一棵树，从而G是它自身的支撑树。

（2）如果G含圈，任取一圈，从圈中任意去掉一条边，得到G的一个支撑子图G1。如果G1不含圈，那么G1是G的一棵支撑树（因为易见G1是连通的）；如果G1仍含圈，那么从G1中任取一个圈，从圈中再任意去掉一条边，得到G的一个支撑子图G2。如此重复，最终可以得到G的一个支撑子图Gk，它不含圈，则Gk是G的一棵支撑树。

由以上充分性的证明中，提供了一个寻求连通图的支撑树的方法，这种方法称为“破圈法”。

例6.2.2　在图6.1.7（a）中，用破圈法求出图的一棵支撑树。

如图6.2.2所示，此图是图6.1.7（a）的一个支撑子图，且为一棵树（无圈），所以我们找到一棵支撑树，其中，E1=。

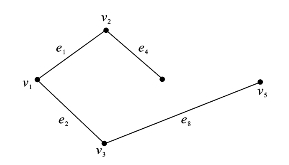
图6.2.2

不难发现，图的支撑树不是唯一的，对于上例若这样做：

如图6.2.3所示，得到图6.1.7（a）的另一棵支撑树，其中E2。

图6.2.3

求图G的支撑树还有另外一种方法“避圈法”，主要步骤是在图中任取一条边e1，找出一条不与e1构成圈的边e2，再找出不与构成圈的边e3……一般地，设e有，找出一条不与构成圈的边ek+1，重复这个过程，直到不能进行下去为止，这时，由所有取出的边所构成的图是图G的一棵支撑树。(www.xing528.com)

定义6.2.3　设是赋权图G=（V，E）的一棵支撑树，称E＇中全部边上的权数之和为支撑树T的权，记为W（T），记

如果支撑树T*的权W（T*）是G的所有支撑数的权中最小者，则称T*是G的最小支撑树，简称为最小树，即

式中对G的所有支撑树T取最小。

求最小树通常用以下两种方法。

（1）破圈法：在给定连通图G中，任取一圈，去掉一条最大权边（如果有两条或两条以上的边都是权最大的边，则任意去掉其中一条），在余图中（是图G的支撑子图）任取一圈，去掉一条最大权边，重复下去，直到余图中无圈为止，即可得到图G的最小树。

例6.2.3　用破圈法求图6.1.7（a）（即图6.1.8）的最小树。

解　取一圈去掉e8。

如图6.2.4所示，得到一棵支撑树，即为所求的最小树T*，W（T*）=1+2+1+2=6。

图6.2.4

（2）避圈法（Kruskal算法）：在连通图G中，任取权值最小的一条边（若有两条或两条以上权相同且最小，则任取一条），在未选边中选一条权值最小的边，要求所选边与已选边不构成圈，重复下去，直到不存在与已选边不构成圈的边为止，那么已选边与顶点构成的图T就是所求最小树。

算法的具体步骤如下：

第1步：令i=1（空集）。

第2步：选一条边中不含圈的所有边e（e∈E\Ei））中权最小的边，如果这样的边不存在，则T=（V，E i-1）是最小树。

第3步：把i换成i+1，返回第2步。

例6.2.4　用避圈法求图6.1.7（a）（即图6.1.8）的最小树。