基本定义和定理大汇总

图论中的图由点和边组成，点和边取决于实际问题的需要。例如，在“哥尼斯堡的七座桥”问题中，点表示陆地和岛屿，边表示桥。而在“绕行世界”问题中，点则表示城市，边则表示城市之间的通路。又如，若干球队比赛，可以用点表示球队，点间的连线表示哪两个球队比赛，如图6.1.5（a）所示，这个图称为无向图。若要表示胜负结果，则可以用箭头表示：箭头指向的一方为负方，如图6.1.5（b）所示，这种图称为有向图。

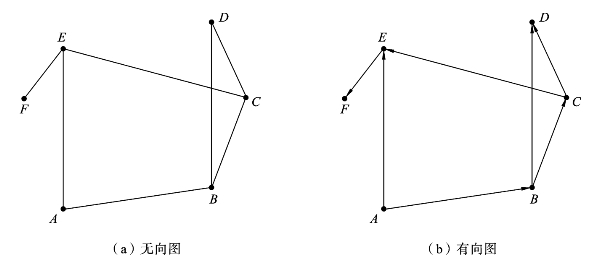
图6.1.5

例如，在图6.1.6中，有8条边，6个顶点，即

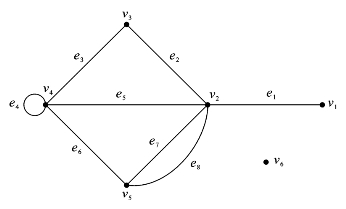
图6.1.6

其中：

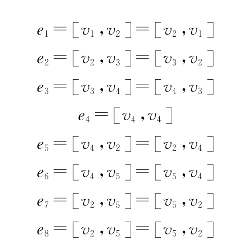
定义6.1.2

（1）顶点数和边数：图中，V中元素的个数称为图G的顶点数，记作或简记为p；E中元素的个数称作图G的边数，记为，或简记为q。

（2）端点和关联边：若，则称点vi，vj是边ei的端点，边ei是点vi和vj的关联边。

（3）相邻点和相邻边：同一条边的两个端点称为相邻点，简称邻点；有公共端点的两条边称为相邻边，简称邻边。

（4）多重边与环：具有相同端点的边称为多重边或平行边；两个端点落在一个顶点的边称为环。

（5）多重图和简单图：含有多重边的图称为多重图；无环也无多重边的图称为简单图。

（6）次：以vi为端点的边的条数称为点vi的次，记作。

（7）悬挂点和悬挂边：次为1的点称为悬挂点；与悬挂点相连的边称为悬挂边。

（8）孤立点：次为零的点称为孤立点。

（9）奇点与偶点：次为奇数的点称为奇点；次为偶数的点称为偶点。

例如，在图6.1.6中，，v4与v3是e3的端点，e3是v4和v3的关联边；v2与v5是邻点，e3与e2是邻边；e7与e8是多重边，e4是一个环；图6.1.6是一个多重图；v1是悬挂点，e1是悬挂边；v6是孤立点；v2是奇点，v3是偶点。

定理6.1.1　图中，所有点的次之和是边数的两倍，即

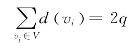
定理6.1.1是显然的，因为在计算各点的次时，每条边都计算了两次，于是图G中全部顶点的次之和就是边数的两倍。

定理6.1.2　任一图中，奇点的个数为偶数。

证明　设V1，V2分别是G中奇点和偶点的集合，由定理6.1.1可知

定义6.1.4

（1）回路：一条闭的链称为回路。

（2）通路：一条开的初等链称为通路。(www.xing528.com)

（3）简单的回路和初等回路：若回路中的边都互不相同，则称为简单回路；若回路中的边和顶点都互不相同，则称为初等回路或圈。

定义6.1.5　一个图G的任意两个顶点之间，如果至少有一条通路将它们连接起来，则这个图G就称为连通图，否则称为不连通图。

例如，图6.1.6中，v1与v6没有一条通路把它们连接起来，故此图是不连通图。本章以后讨论的图，除特别声明外，均指连通图。

定义6.1.6

（4）支撑子图：若G1是G2的部分图，且G1是连通图，则称G1是G2的支撑子图。

（5）生成子图：若G1是G2的真子图，且G1是不连通图，则称G1是G2的生成子图。

例如，图6.1.7中，图（b）是图（a）的真子图，图（c）是图（a）的部分图，图（d）是图（a）的支撑子图，图（e）是图（a）的生成子图。

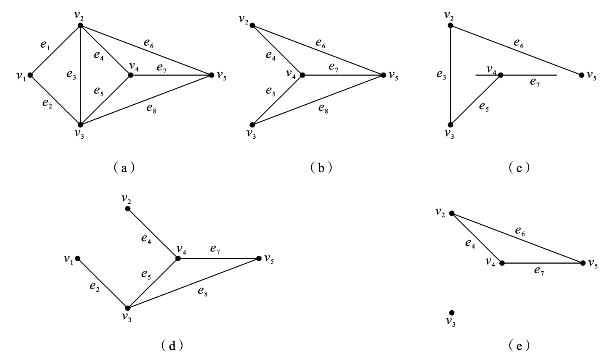
图6.1.7

定义6.1.7　设中，对于任意一条边，如果相应都有一个权值W（e），则称G为赋权图，W（e）称为边e的权。

图6.1.8是一个赋权图。

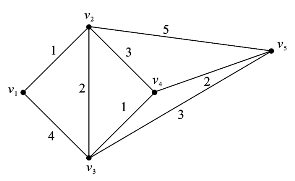
图6.1.8

可见，赋权图不仅指出各点之间的邻接关系，而且也表示各点之间连接的数量关系，所以赋权图在图的理论及应用方面有着重要的地位。

在很多实际问题中，事物之间的联系是带有方向性的。如图6.1.5（b）所示，箭头的方向指向负方的球队。又如图6.1.9所示，v1表示某一水系的发源地，v6表示这个水系的入海口，图中的箭头则表示各支流的水流方向，图6.1.9是水系流向图。图6.1.5（b）和图6.1.9称为有向图。下面给出有向图和赋权有向图的正规定义。

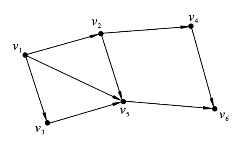
图6.1.9

定义6.1.8　设是由n个顶点组成的非空集合，A=是由m条边组成的集合，且有A中元素ai是V中的一个有序元素对（vi，vj），则称V和A构成了一个有向图，记作G=（V，A），ai=（vi，vj）表明vi和vj分别为边ai的起点和终点，称有方向的边ai为弧（在图中用带有箭头的线表示）。

例如，图6.1.9中，（v1，v2），（v1，v3），（v2，v5）都是A中的元素，A是弧的集合。

与无向图类似，在有向图中也可以定义多重边、环、简单图、链等概念。只是在无向图中，链与路、闭链与回路概念是一致的，而在有向图中，这两个概念却不能混为一谈。概括地说，一条路必定是一条链。然而在有向图中，一条链未必是一条路，只有在相邻的两弧的公共结点是其中一条弧的终点，同时又是另一条弧的始点时，这条链才能叫做一条路。

例如，图6.1.9中是一条链，也是一条路，而是一条链但不是一条路。

图6.1.10是表示某地区交通运输公路分布、走向及相应费用的有向图。箭头表示走向，箭头旁边的数字表示费用。这类图称为赋权有向图。

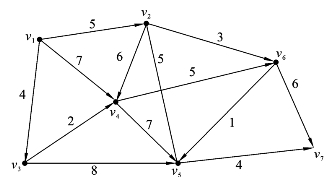
图6.1.10

定义6.1.9　设在有向图G=（V，A）中，对于任意一条弧，如果相应都有一个权值W（aij），则称G为赋权有向图，W（aij）称为弧aij的权，简记为Wij（权可以表示距离、费用和时间等）。

在实际工作中，有很多问题的可行解方案都可以通过一个赋权有向图来表示，例如，物流渠道的设计、物资运输路线的安排、装卸设备的更新、排水管道的铺设等。所以，赋权图被广泛应用于解决工程技术及科学管理等领域的最优化问题。

通常，我们称赋权图为网络，称赋权有向图为有向网络，称赋权无向图为无向网络。我们讨论的目标是要解决这些网络的计划与优化问题，其数学方法是：最小支撑树、最短路、网络最大流、最小费用等问题的求解方法。下面逐节加以介绍。