古典问题探讨：图6.1.1的困扰

1.“哥尼斯堡的七座桥”问题

图论的研究已有200多年的历史，早期图论与“数学游戏”有着密切关系，“哥尼斯堡的七座桥”问题便是其中之一。

200多年前的东普鲁士有一座哥尼斯堡城（现属俄罗斯加里宁格勒），城中有一条河叫普雷格尔河，河中有两个岛屿共建七座桥，如图6.1.1所示。平时城中居民大都喜欢来这里散步，有人提出这样一个问题：一个散步者能否经过每座桥恰好一次最后回到原出发点。

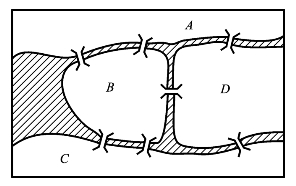
图6.1.1

当时有许多人都探讨了这个问题，但不得其解。著名数学家欧拉（Euler）于1736年发表了图论方面的第一篇论文，将此难题化成了一个数学问题：用点表示两岸或小岛，用点之间的连线表示陆地之间的桥，这样就得到了图6.1.2所示的一个图。从而，问题变为：在这个图中，是否可能从某一点出发只经过各条边一次且仅仅一次而又回到出发点？即一笔画问题。

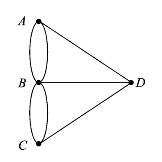
图6.1.2(www.xing528.com)

欧拉否定了这种可能性，原因是图中与每一个点相关联的线都是奇数条（要回到出发点，每一点相连的边，必须是偶数条）。

2.哈密尔顿图

1859年，哈密尔顿提出了一种游戏：在一个实心的12面体（见图6.1.3）的20个顶点上标以世界上著名的城市名称，要求游戏者从某一城市出发，遍历各城市恰恰一次而返回原地，这就是“绕行世界问题”。我们可以按此问题作出如图6.1.4所示的图形，该问题变为：从某一点出发寻找一条路径，过所有20个点仅一次，再回到出发点。解决这个问题可以按图中的序号1→2→3→4→…→20→1所形成的一个闭合路径来完成。此路径称为哈密尔顿图。虽然这个“绕行世界问题”解决了，但是由此引出的“对于给定的连通图（见定义6.1.5），让它成为哈密尔顿图的充要条件是什么？”至今尚无定论，这是图论中一个著名的尚未解决的问题。

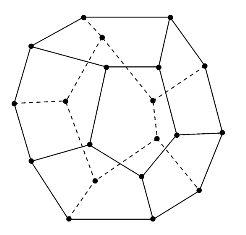
图6.1.3

图6.1.4

由此可见，图论中所研究的图是由实际问题抽象出来的逻辑关系图，这种图与几何中的图形和函数论中所研究的图形是不同的。逻辑关系图的画法具有一定的随意性，在保持相对位置和相互相连关系不变的前提下，点的位置不一定按实际情形来画，线的长度也不一定表示实际的长度，而且画成直线或曲线都可以。通俗地说，这种图是一种关系示意图。