大量实验结果表明,lgε~lgt近似成直线关系,如图7-16所示,并可用下式来描述:
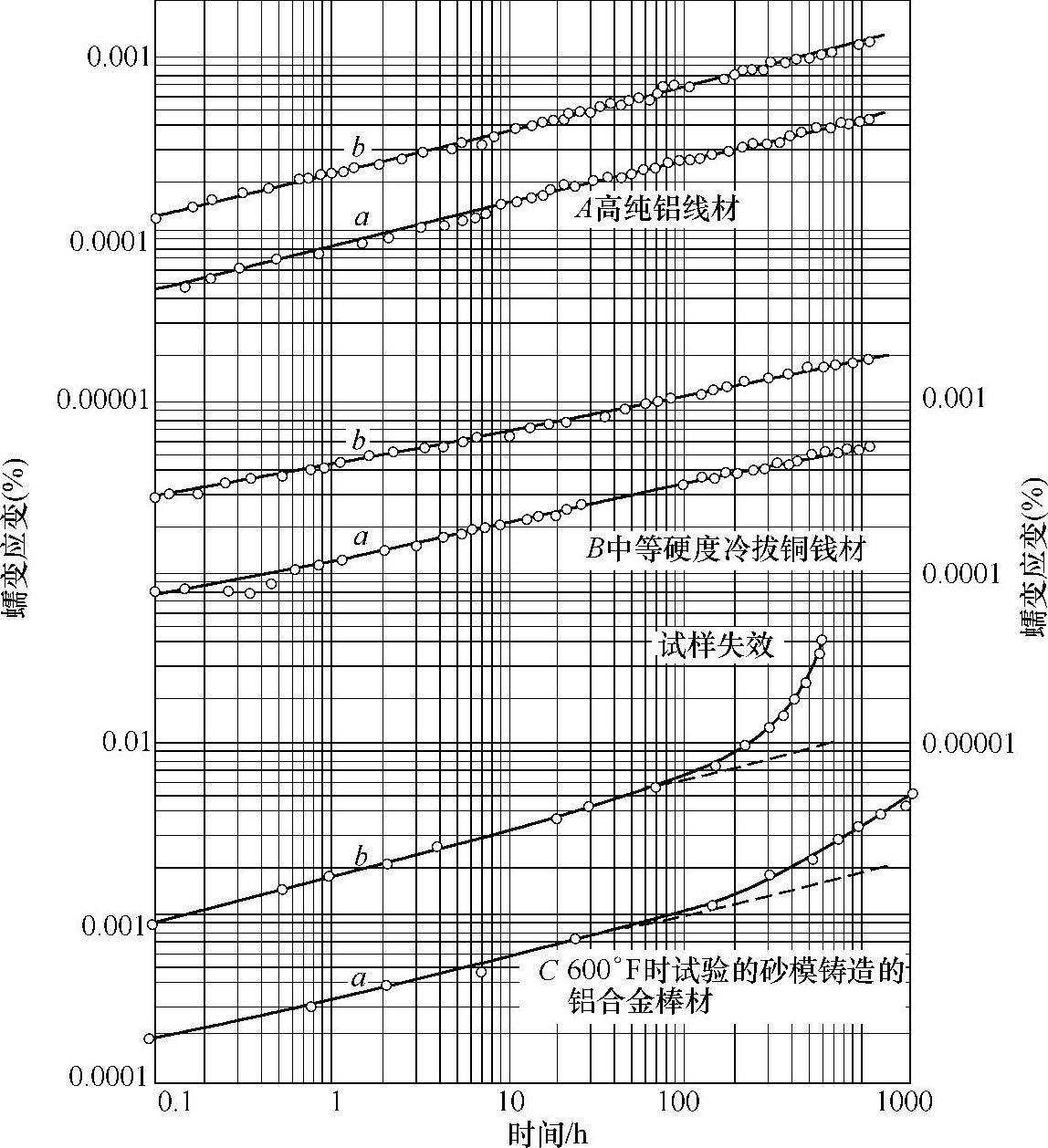
图7-16 lgε-lgt蠕变曲线
lgε=A+αlgt或ε=Atα (7-6)
式中 ε——蠕变真应变;
A、α——与材料、温度有关的常数;
t——时间。
式(7-6)对时间微分,得
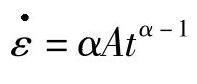
令αA=b,1-α=n,则
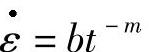
即
由式(7-4)和式(7-7):(https://www.xing528.com)
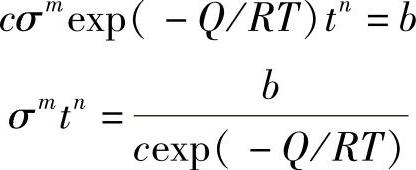
当材料、温度一定时,有
t=Bσ-N (7-8)
式中 B、N——与材料、温度有关的常数。
对数坐标中,t与σ为直线关系,因此当有零件材料在某使用温度(T)下较短时间(一般试验时间为1%~10%所期望的使用寿命)的蠕变性能实验数据时就可图解出B、N值。可利用式(7-8)来预测该材料制成的零件在该温度下各种载荷时的安全寿命。当无足够的实验数据时,只要知道该材料的持久极限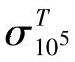 和
和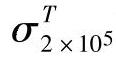 或
或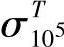 和
和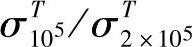 ,可由式(7-8)得
,可由式(7-8)得

同样利用式(7-9)和式(7-10),亦可预测出该材料制成的零件在该温度下不同受力时的寿命。
式(7-10)中考虑到有时要求使用寿命超过105 h及N值在长寿命时可能发生变化的情况。因为使用过程中,由于组织构成的变化,N值的变化是完全可能的(见图7-17),处理实际问题应加以注意。
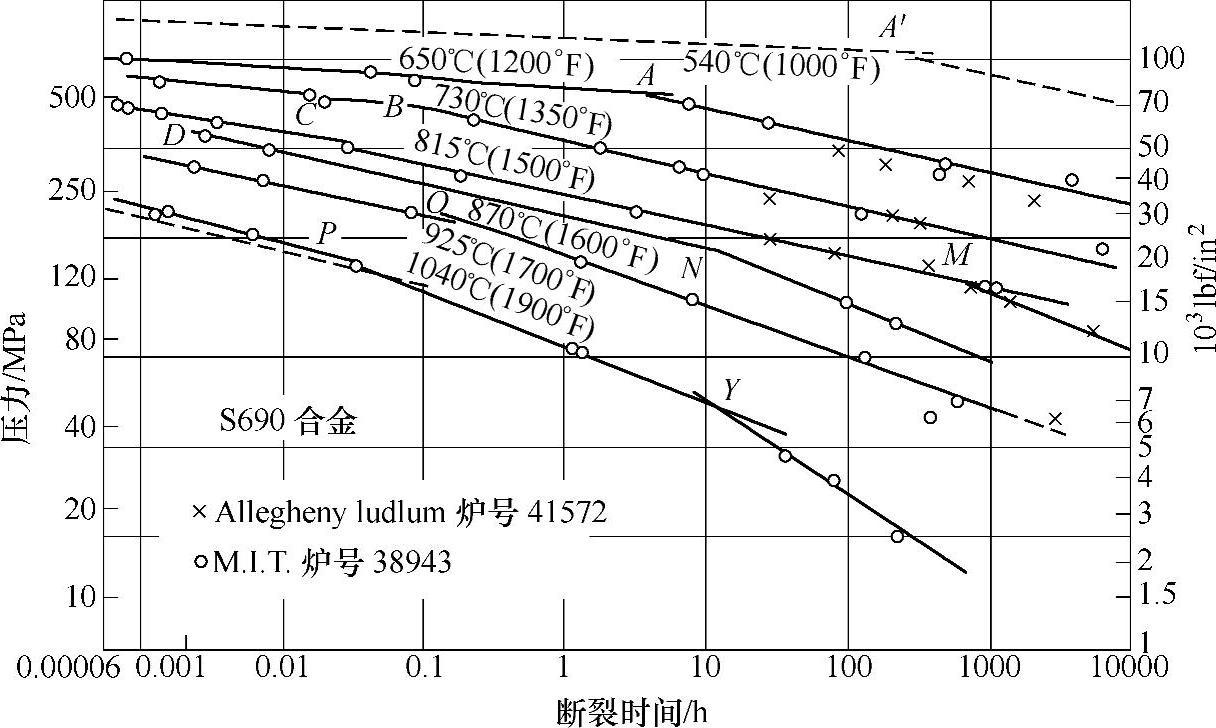
图7-17 铁基合金lgσ-lgt蠕变曲线
进行寿命预测还有许多方法,如正常应力短时实验法(Abrige Method of Creep Testing)、高应力加速试验法(Mechanical Acceleration Method of Creep Testing)和高温加速试验法(Thermal Acceleration Method of Creep Testing)等实验图解法以及Larson-Miller参数法和Manson-Haferd参数法等分析法,可参见J.A.Collins的《Failure of Materials in Mechanical Design》(Analysis Prediction Prevention)(1981)。实际工作中可根据具体情况进行选用。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




