圆柱齿轮接触强度赫兹公式及推导

（1）最大接触应力的计算公式 1881年赫兹（Hertz）应用牛顿势函数，推导出了两弹性圆柱体接触区表面最大接触应力的计算公式。推导中的前提和假设条件是：两圆柱体为无限长的、均质的、各向同性的弹性体；其变形后的接触面与圆柱表面相比是极其微小的；作用力为静载荷、与接触面垂直，且沿圆柱体的长度方向均匀分布（这样就可以简化作平面的应力、应变分析）。

如图4-20所示，长度为L，半径为ρ₁、ρ₂的两平行圆柱体在加载前为线接触，当加上法向力F之后，接触处变形成一个宽度为2s的矩形面积。我们取其某一截面进行应力分析，则作用于该截面上的法向力即为F/L。在截面上的应力呈椭圆分布：

即

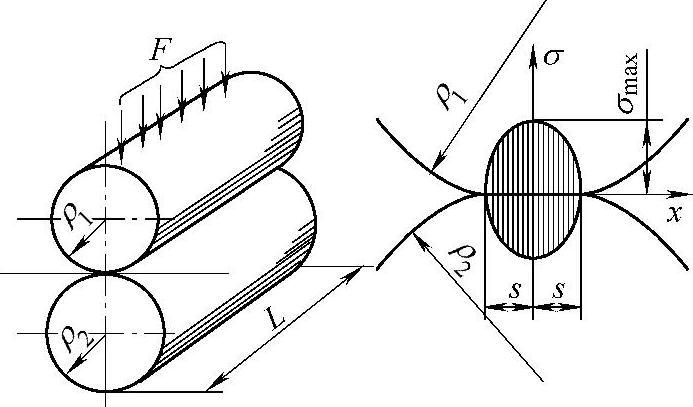
图4-20 两圆柱体的接触应力

则在该截面内，作用在2s宽度上的应力之和，就是这半个椭圆的面积

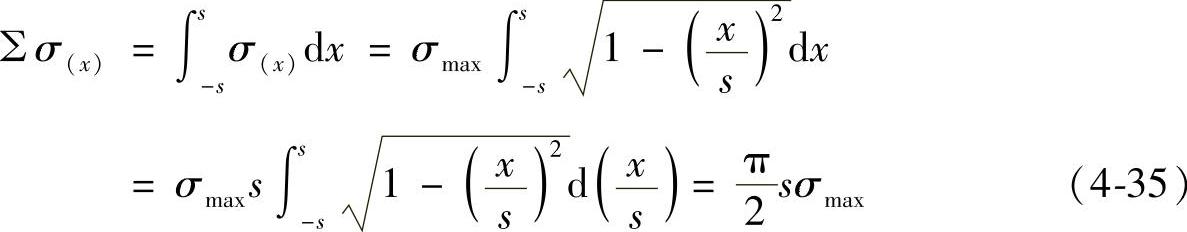
我们已知，此时作用在该截面内的法向力F/L应与∑σ_（x）相等，即

则最大压应力为

又根据弹性力学可知，接触变形宽度的一半为

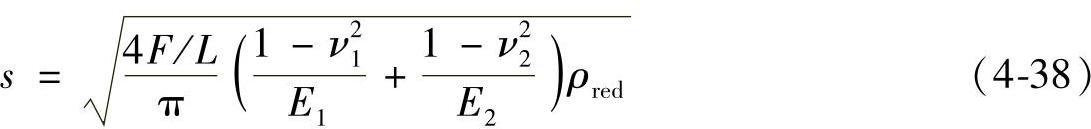
将式（4-36）代入式（4-35），可得出

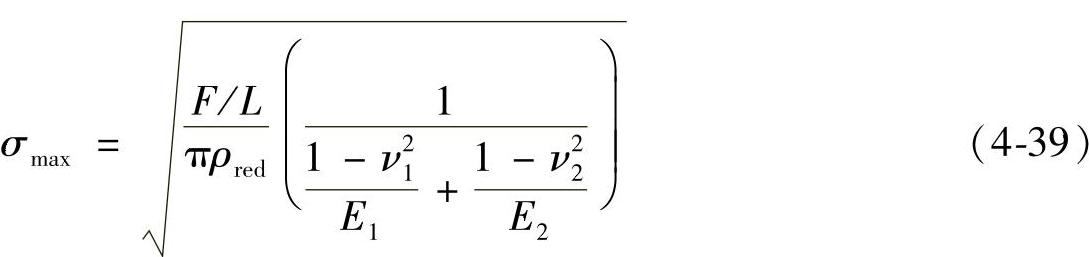
式中ν₁、ν₂——圆柱体1与圆柱体2材料的泊松比；

E₁、E₂——圆柱体1与圆柱体2材料的弹性模量；

ρ_red——当量曲率半径，;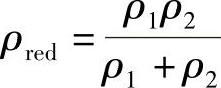

ρ₁、ρ₂——分别为两圆柱体的曲率半径；

F/L——作用在圆柱体单位长度上的法向力。

式（4-40），即为赫兹公式的一般表达形式，其计算值σ_max称为赫兹应力。

（2）齿面接触应力基本值σ_HO计算公式的建立 齿面的啮合过程，就对像两个曲率半径在随时变化着的圆柱体的接触过程，因此，可以赫兹公式为基础建立σ_HO的计算公式。这里可以说为基础，是因为实际齿轮传动中齿面接触状况、工作条件等情况，与赫兹公式推导时的前提和假设是不同的，要复杂得多。

在以赫兹公式为基础建立接触应力基本值σ_HO的计算公式之前，必须首先明确下面四个问题。

1）在不同的啮合位置，齿面接触点处的曲率半径是各不相同的，我们由式（4-40）可以看出，曲率半径的不同，或者当量曲率半径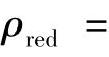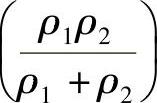的不同，影响着赫兹应力的大小。

由图4-21可知，在有效啮合线长AE范围内，考虑到当量曲率的变化和载荷分配的综合影响，小齿轮的单对齿啮合区下界点B处的赫兹应力为最大，节点C处次之；但对于小齿轮齿数Z₁大于20的一般情况来说，C点的赫兹应力与B点的赫兹应力相比相差甚微。

此时还必须考虑到齿面间的相对滚动、滑动及由此造成的润滑状况对齿面承载能力的影响。

图4-21 外啮合传动的啮合状态

并且，从计算上来说，节点处的当量曲率半径不随重合度而变化，因此按节点C处计算赫兹应力比较方便。

综合考虑以上原因，目前大多数学派都选择节点作为危险点进行接触强度计算。

在小齿轮齿数Z₁<20、当量曲率的影响较为显著时，若需精确计算接触强度时，可以按小轮的单对齿啮合区下界点B作为危险点进行计算。

节点C处的曲率半径，由图4-21可知：

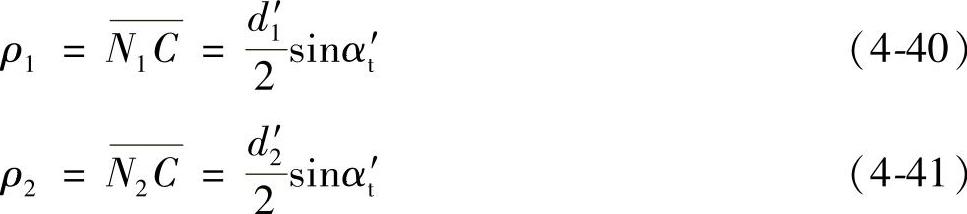
式中 d₁′、d₂′——小轮、大轮的节圆直径；

α_t′——端面内节圆处压力角。

当量曲率为

我们注意到，式（4-42）仅是对外啮合齿轮的情况，为把内啮合齿轮的情况也包括起来，我们把式（4-42）改写成下面一种统一的形式：

式中的“+”号用于外啮合传动，“-”号用于内啮合传动。

我们还应当注意到，式（4-43）是在直齿轮的情况下分析和推导出来的。对于斜齿轮来说，在C点两接触齿面的实际曲率半径，应是其法截面内的数值。图4-22所示情况是一个平行于齿轮轴心线的水平视图，如果由上向下俯视，则啮合线N₁N₂就是一个啮合平面，如图4-22所示。

该啮合平面上的斜粗实线，即是轮齿的接触线。此时的直线N₁N₂即是端截面与啮合平面的交线；直线N₁′N₂′即是斜齿轮的法向截面（垂直于接触线）与啮合平面的交线；C点为节点。

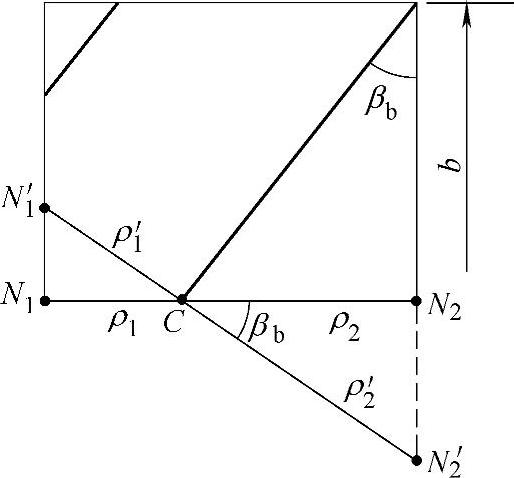
图4-22 斜齿轮的啮合平面

我们知道N₁C是端面内小齿轮在节点C处的曲率半径ρ₁，N₂C是端面内大齿轮在节点C处的曲率半径ρ₂（图4-21亦可看出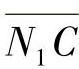），是法面内小齿轮在节点C处的实际曲率半径ρ₁′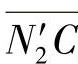，是法面内大齿轮在节点C处的实际曲率半径ρ₂′。

我们还知道，接触线与宽度方向（即齿轮圆柱体的母线方向）的夹角为基圆螺旋角β_b，同时由于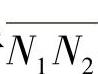垂直于齿宽方向，N₁′N₂′垂直于轮齿接触线，因此，N₁N₂与N₁′N₂′的夹角也等于β_b。

式（4-44）、式（4-45）说明，斜齿轮C点处的实际曲率半径，可以由端面内C点处的曲率半径来表示。

则斜齿轮在C点实际当量曲率为(www.xing528.com)

将式（4-46）代入式（4-43）可得出

可以看出，式（4-47）是适用内、外啮合的直齿、斜齿轮的统一形式。

我们还可以看出，式（4-47）中的节圆直径d₁′、d₂′是一个需要计算的量，为了利用原始的几何参数，方便运算使用，我们可做如下代换：

且

d₂=d₁u （4-51）

则有

将式（4-48）、式（4-52）代入式（4-47）并整理，即可得出我们所需要的当量曲率的通用表达形式

式中d₁——小齿轮直径（mm）；

u=z₂/z₁——齿数比；式中“+”号用于外啮合传动，“-”号用于内啮合传动；

β_b——基圆螺旋角；

α_t——端面齿形角；

α_t′——端面啮合角。

2）接触线长度L的确定。众所周知，在端面重合度ε_α和纵向重合度ε_β的影响下，由于同时有几对齿参与啮合，所以导致总的承载齿宽B（各对轮齿上承载齿宽的总和）大于齿轮的齿宽b。两者之间在量值上关系可用一个函数式来表示：

式中 z_ε——我们称为重合度系数，表示在端面重合度ε_α和纵向重合度ε_β的作用下，实际的总承载齿宽B和齿轮齿宽b的比值（在式（4-54）中写成z²_ε，是为了公式表达的方便，将来可移至根号外）；

B——同时啮合的各对轮齿上承载齿宽的总和，当然，这里是一个概率的平均值（实际上，在不同的啮合位置上，B是不断变化的）。

又由图4-22可知，轮齿的接触方向与齿宽方向的夹角为基圆螺旋角β_b。所以，总的接触线长度L就可表示为

当然，这里的L也同B一样，是个概率的平均值。

3）法向力的确定。在节点C处的受力状况，如图4-23所示。

图中，F′_t为端面内节圆周上的切向力，F′_bt为端面内基圆周上的切向力，F_b′_n为法面内基圆周上的切向力，即作用在节点C处齿廓上的法向力，α′_t为端面内节点处的压力角（即端面内的啮合角），β_b为基圆螺旋角。

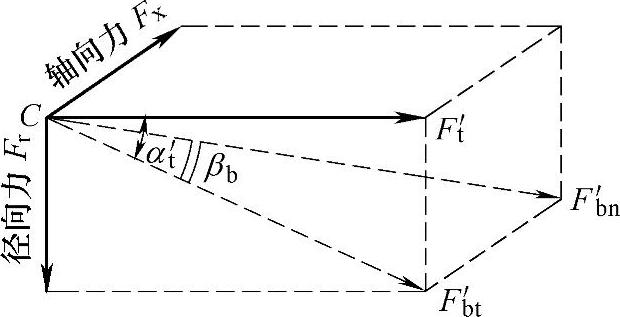
图4-23 斜齿轮受力分析

由图4-23可知，

转矩

所以

由式（4-48）或式（4-49）可知，节圆直径d′与分度圆直径d有如下关系

将此关系式代入式（4-58），即可得

将式（4-60）代入式（4-56），则

由式（4-52）和式（4-58）我们就可以得出单位接触长度上的法向力为

4）接触线上载荷分布状况的影响。斜齿轮由于螺旋角的作用，轮齿上的接触线是由齿顶到齿根倾斜着的。试验和经验都证明，接触线的倾斜，会给齿面的接触强度带来有利的影响，也就是说，会使节点的实际接触应力比用赫兹公式计算的结果要小。

考虑这一影响，为了消除这一误差，我们要在赫兹应力公式中引入一个修正系数，称之为螺旋角系数z_β。

在考虑和分析了以上4点之后，我们就可以在赫兹公式的基础上，建立了接触应力基本值σ_HO的公式。现将第4点讨论的结论和式（4-54）及式（4-60）代入第式（4-40），便可得出

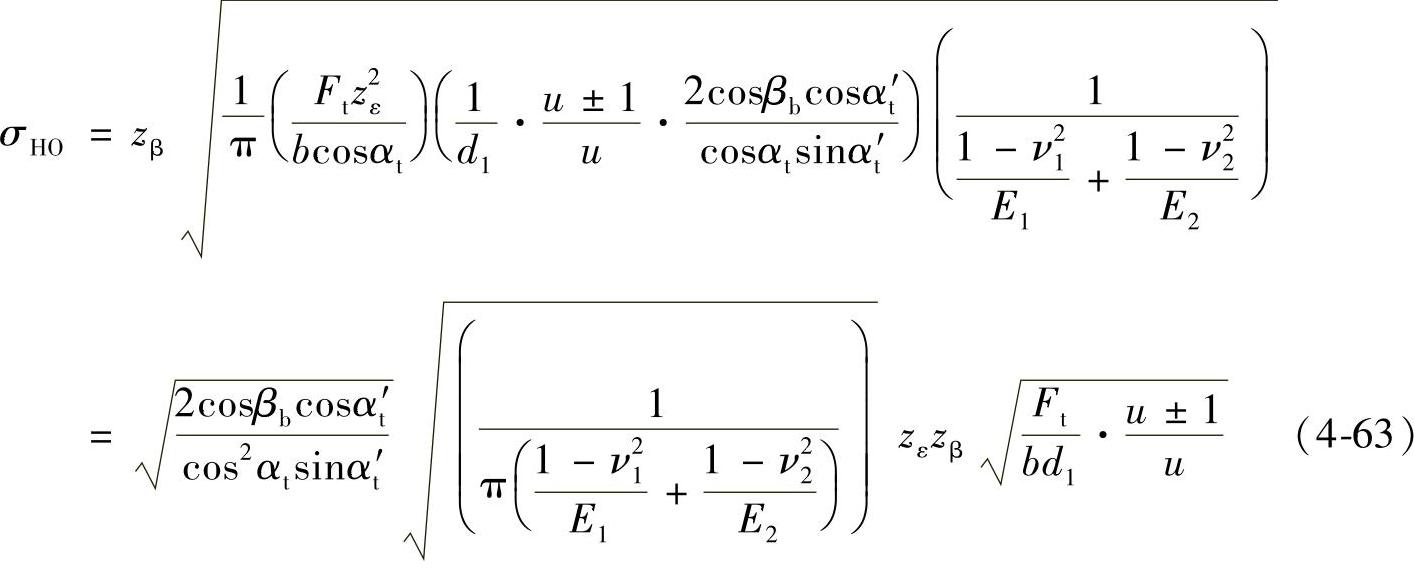
其中 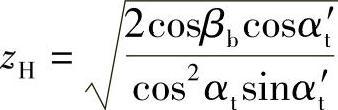，为节点区域系数，仅与齿轮的几何参数有关，包括着节点曲率半径计算的因素和节圆处齿廓法向力计算的因素。

，为弹性系数，仅与材料的特性（泊松比和弹性模量）有关。于是便得齿面接触应力基本值σ_HO的计算公式为

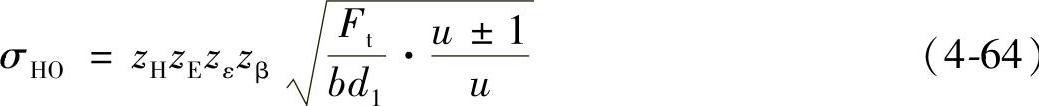
这就是齿轮强度计算国标中齿面接触应力基本值的计算公式。