随机载荷谱下的疲劳寿命计算优化

受随机载荷作用的构件，其寿命一般可用线性累积损伤理论计算。由于它的应力变化是不规则的，如图4-15所示，经整理后可以简化为有规律的应力谱，如图4-15中（σ）1，（σ）2，…，（σ）i，…，（σ）n为各应力水平的大小，n₁，n₂，…，n_i，…，n_n为各应力水平下的循环数。

设构件在常应力幅（σ）1作用下直到破坏的循环数为N₁（图4-16），则

图4-15 随机载荷谱示意图

总的周期数为λ（图4-13），则构件受到应力（σ）1的损伤率为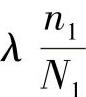，同理应力（σ）i，…，（σ）n对构件的损伤率分别为。

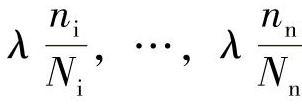线性累积损伤理论假设：当各级应力水平对构件的损伤率总和达到1时，构件即发生破坏，即

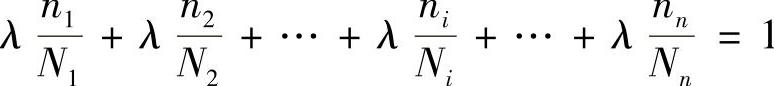（4-16）

一般情况下可写成(www.xing528.com)

试验证明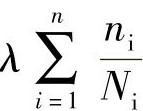一般不等于1，而是大于1的某一数值a，a与材料性质及应力历程有关，称为抗过载系数。

图4-16 损坏的循环数

于是构件安全工作的总周期数λ为

这样知道每一个载荷变化周期内的载荷谱，就可以利用上式求出总的载荷变化周期数λ，即可能的疲劳寿命。

Palmgren-Miner线性累积损伤法则有一定误差，甚至有时是偏不安全的，再加上S-N曲线是统计规律，同时使用载荷的可能变化，材料性能又有一定的分散性，故往往规定将计算出的疲劳寿命除以寿命安全系数n_N，n_N一般取4～7.5，视具体情况而定。