低周疲劳寿命估算方法探析

低周疲劳的应力-应变回线如图4-12所示。由图可见：

弹性应变幅

图4-12 低周疲劳应力-应变回线

塑性应变幅Δε_p=TQ （4-5）

总应变幅Δε_T=Δε_e+Δε_p （4-6）

而从实验得到

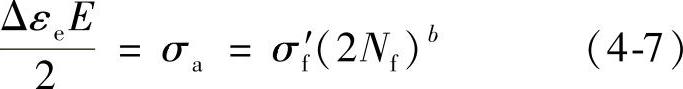
式中 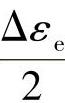——弹性应变幅；

E——弹性模量；

σ_a——应力幅；

σ_f′——疲劳强度系数，其值为2N_f=1（一个载荷循环）时应力轴上的截距，且σ_f′≈σ_f（单调拉伸断裂强度）；

N_f——失效前载荷循环次数；

2N_f——失效前载荷反向次数；

b——疲劳强度指数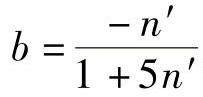，，n′为循环应变硬化指数。一般碳钢b=-0.1，铝合金b=-0.15，钛合金b=-0.08

根据Manson-Coffin关系可得：

式中 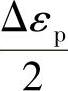——塑性应变幅；(www.xing528.com)

ε_f′——疲劳塑性系数，其值为2N_f=1（一个应力循环）时，在应变轴上的截距。ε_f′=（0.35～1.0）ε_f（ε_f为单调拉伸断裂真应变），作为一级近似往往取ε_f′=ε_f；

2N_f——失效前应变反向次数；

c——疲劳塑性系数。为一材料常数，一般为-0.5～-0.7，且亦可由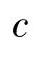估算得到，n′为循环应变硬化指数。

由式（4-4）和式（4-5）可知，高韧性合金低周疲劳寿命长，而高强度合金高周疲劳寿命长。

Manson等证明，承受给定应变幅的材料其疲劳抗力应用弹性应变分量与塑性应变分量的叠加来估算。用式（4-7）和式（4-8）代入式（4-6），得Morrow公式：

从式（4-19）可得图4-13a，图4-13b为18Ni钢的实验曲线，可见实验结果与上述分析一致。

另外，Δε_T-N_f曲线亦可由四点法和能用斜率法来近似。

四点法：在对数坐标中，Δε_c-N_f曲线可由点和点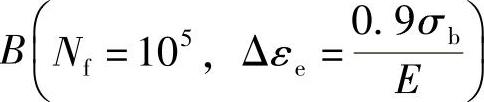组成的直线来代表（σ_n为拉伸断裂真应力，σ_b为拉伸强度极限）；Δε_p-N_f曲线可由点和点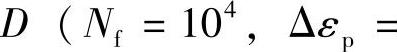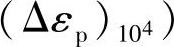的联线来代表（ε_f为断裂真空变，，Δε_c^*为Δε_c-N_f曲线上N_f=10⁴时的应变幅值）。这种方法叫四点法，可不必进行疲劳试验。工程上把弹性线与塑性线的交点定为低、高周疲劳的分界点。

图4-13 弹、塑性应变寿命曲线叠加得到总应变寿命曲线

a）叠加图解 b）18Ni钢的实验曲线

通用斜率法：Manson则由29种材料的试验结果得出弹性线、塑性线均有公用斜率，且分别为-0.12和-0.6，于是得到

此法称为通用斜率法，其精度与四点法相近。

由此可见，当无足够可参考的疲劳试验数据时，可由材料的拉伸性能数据估算出该材料在某一定应变幅值下的疲劳寿命（N_f）。