轮齿离散化模型及其影响因素分析

近30年来，国内、外不少作者应用有限元法计算过齿轮的弯曲应力，不同的作者采用的各种离散化模型如图3-19所示。

图3-19a～图3-19c用的是三节点三角形单元，这种单元的特点是容易灵活拟合曲线边界，计算时间短，但由于采用线性位移插值，应力在单元内是常量，所以为了满足计算精度，必须布置大量的单元。

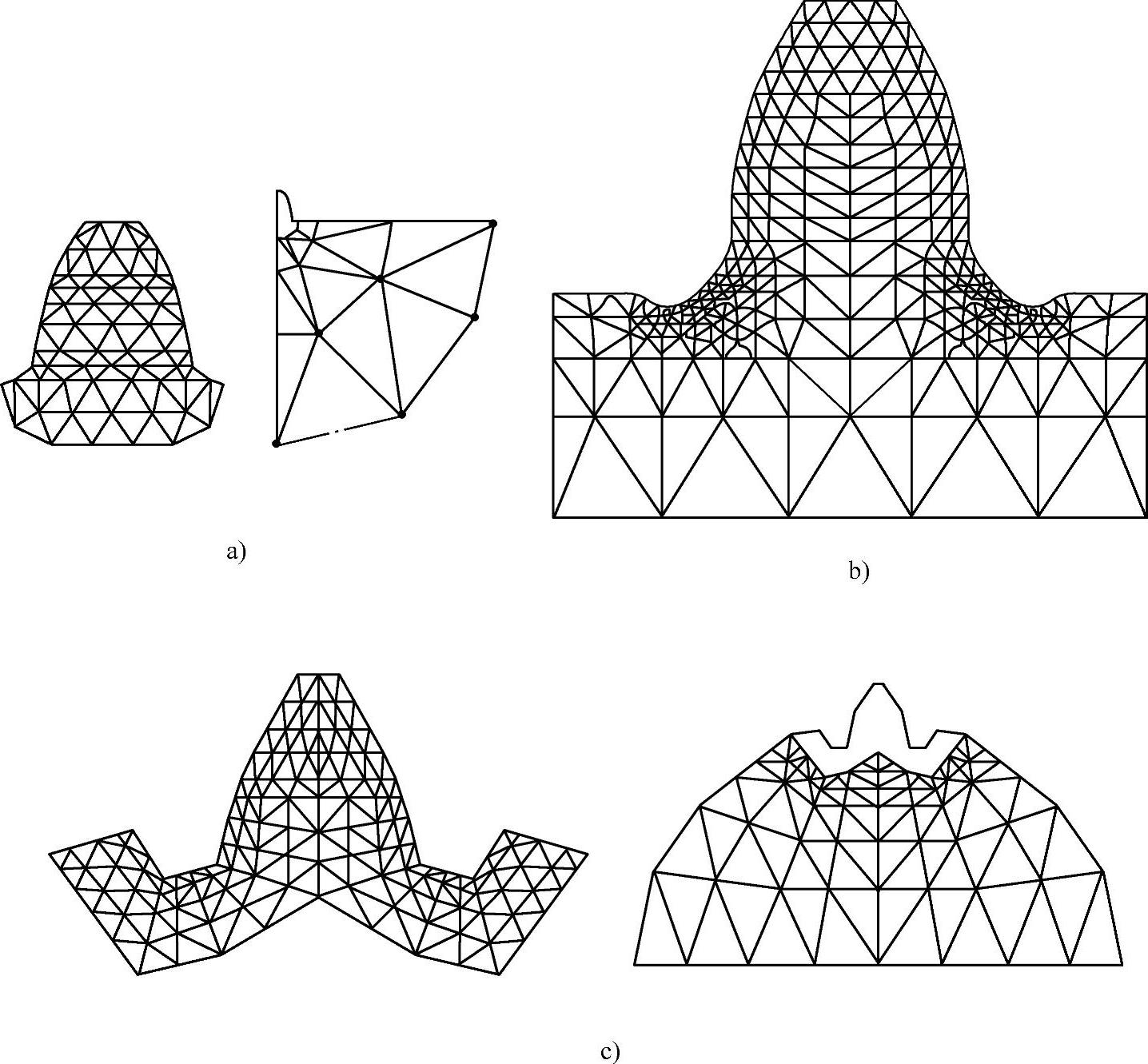
图3-19 轮齿离散化模型

a）三角形三节点单元 日本东北大学户部俊美 b）三角形三节点单元 清华大学蒋孝煜、高维山 c）三角形三节点单元 德国Daimler-Benz公司

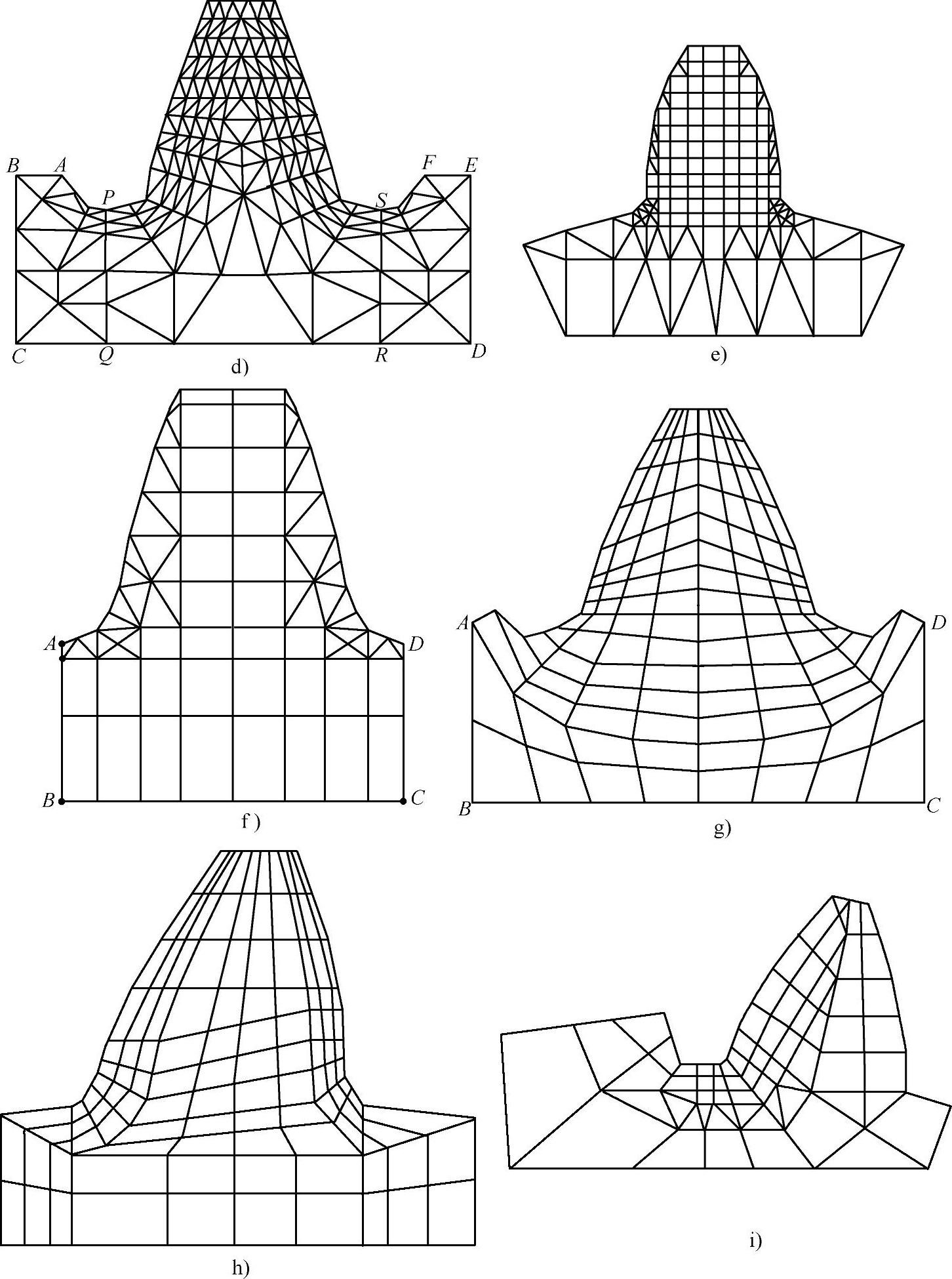
图3-19 轮齿离散化模型（续一）

d）三角形六节点单元 法国CETIM Chabert e）矩形和三角形单元组合 美国Wallace f）矩形和三角形单元组合 上海交通大学黄瑞清g）四边形四节点单元 德国达姆斯达特工业大学 h）四边形四节点单元 美国格里森公司i）四边形三角形单元组合 德国弗利德利希司齿轮厂

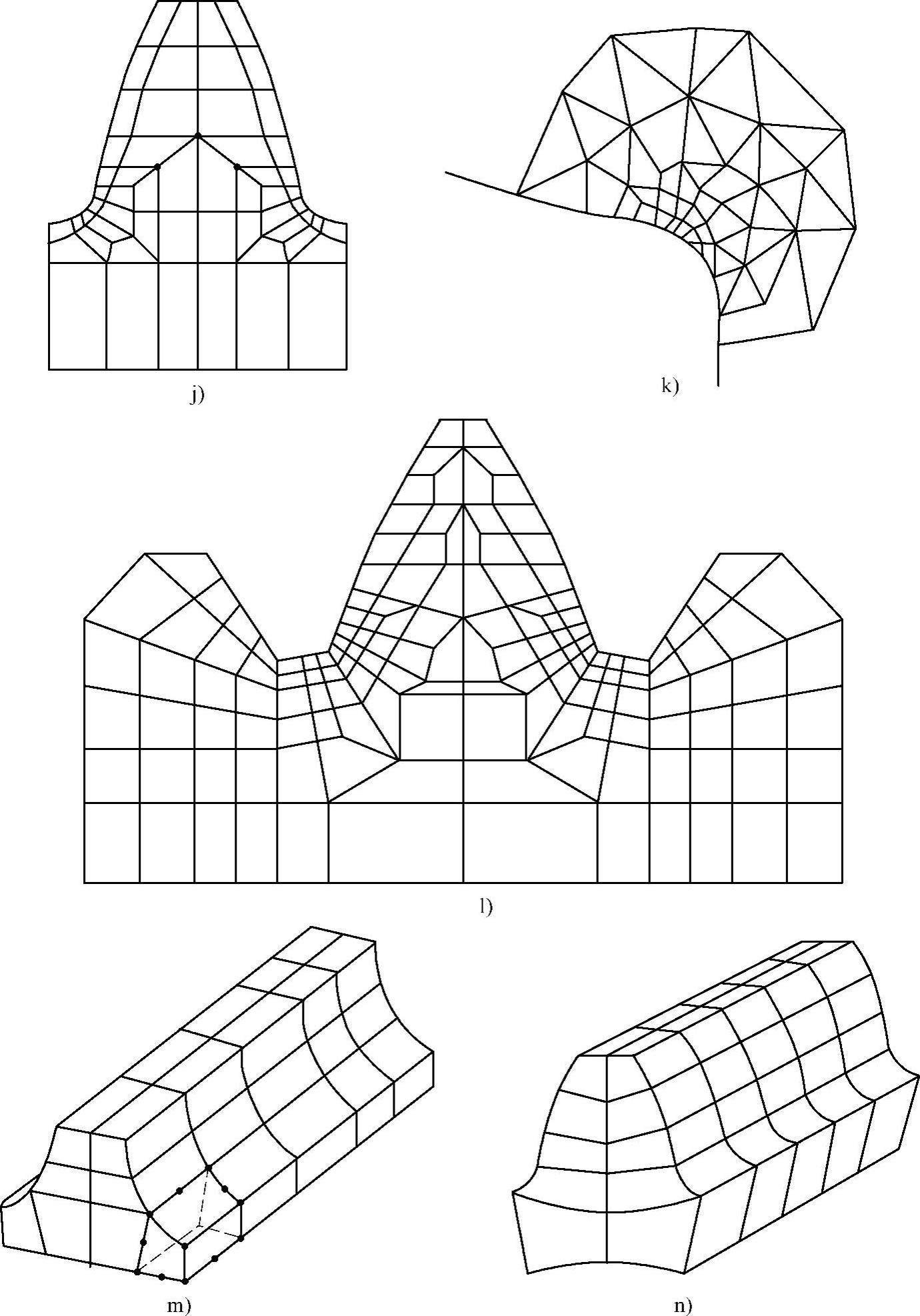
图3-19 轮齿离散化模型（续二）

j）四边形八节点单元 上海科技大学陆思齐k）八节点四边形和六节点三角形单元组合 上海交通大学王统l）四边形十二节点单元 德国MTU公司 m）二十节点立体单元 美国Westland直升飞机公司n）二十节点立体单元 清华大学董烈铮

图3-19d用的是三角形六节点单元，这种单元在三角形每边上多加一个节点，使单元内应力按线性变化，这比三节点单元更接近于实际应力分布状况。

图3-19e、图3-19f用的是矩形单元和三节点三角形单元的组合。矩形单元的应力是按线性变化的，但不能适应曲线边界，所以边界上用三角形单元填补。

图3-19g、图3-19h用的是任意四边形单元，这种单元是由矩形单元经过坐标变换而得到的，可以适应曲线边界。但若和三角形单元相结合可使小单元容易过渡到大单元。

图3-19i、图3-19j用的是八节点四边形单元，这种单元应力是按二次曲线变化的，所以用较少单元可以达到较高的计算精度，但是计算时间长是它的缺点。

图3-19k是用八节点四边形和六节点三角形组合，对齿根应力集中区域进行加密划分以作指定边界位移的二次计算。

图3-19l用的是十二节点四边形单元，其计算精度比八节点的四边形单元高，但计算时间更长。

图3-19m、图3-19n是用二十节点曲面六面体单元进行轮齿的三维应力分析。

美国格里逊公司的Wileox L.，法国CETIM的Chabert G.和日本东北大学的户部俊美分别计算了大量不同参数的齿轮，在此基础上归纳出简化的应力计算式，户部俊美将之画成曲线，并和AGMA法以及日本的Aida T，Terauchi.Y.所用的保角变换法相比较（图3-20），可以看出，有限元法的曲线比较接近，而AGMA法所算出的应力偏低。清华大学的蒋孝煜、高维山对具有不同曲率半径的齿轮，用图3-19b所示模型进行计算并和AGMA法对比，也得到后者的计算值偏低的结论（图3-21）。

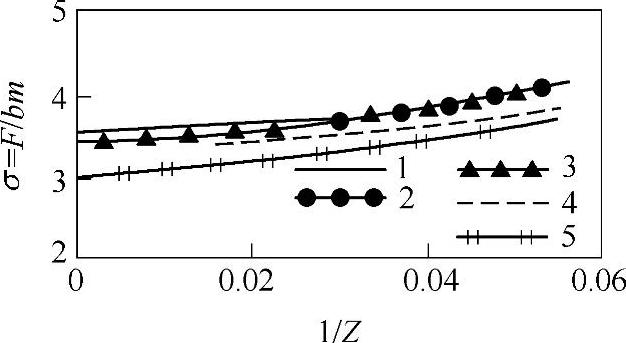
图3-20 应力计算比较

1—户部 2—Wilcox L 3—Chabert G. 4—Aida T.Terauchi Y. 5—AGMA(www.xing528.com)

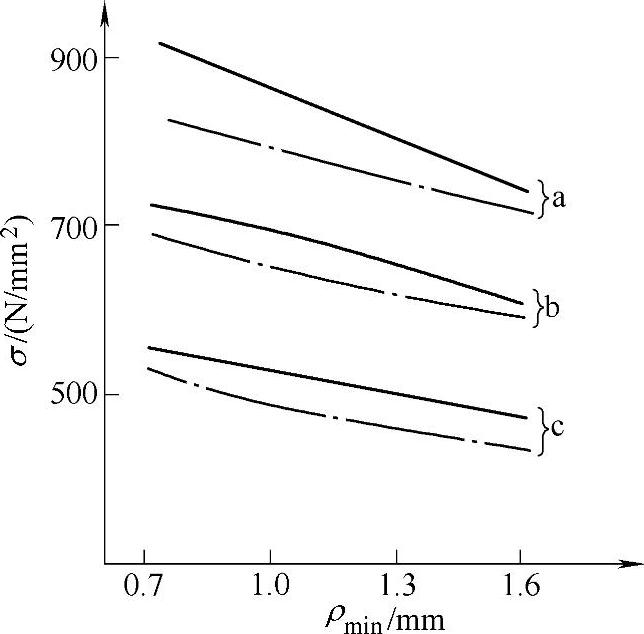
图3-21 有限法与AGMA法的比较——有限法（清华大学蒋孝煜、高维山）

AGMA法 a—载荷作用在齿尖上 b—载荷作用在一对齿啮合的最高点 c—载荷作用在一对齿啮合的最低点

德国Winter H.为了检验ISO法的准确程度，建议各国计算者对一个共同齿形（图3-22）进行计算，以便于进行对比，表3-2就是各国计算者用各种方法计算的结果。图3-19a、图3-19c、图3-19d、图3-19g、图3-19i和图3-19l就是表3-2中的有关计算者利用的有限元模型。户部俊美将表3-2整理成图3-23，可以看出，模型中总自由度越高，计算精度也越高，从图3-23也可以看出ISO的计算值偏高。可见，用有限元法的计算结果处在AGMA及ISO两者之间，应该认为它是更符合于实际应力状态。在图3-23中也可以看出Daimler-Benz公司的计算精度最高，而该公司用的却是图3-19c中所示的最简单的三节点三角形单元，可见计算精度并不一定决定于单元型式。

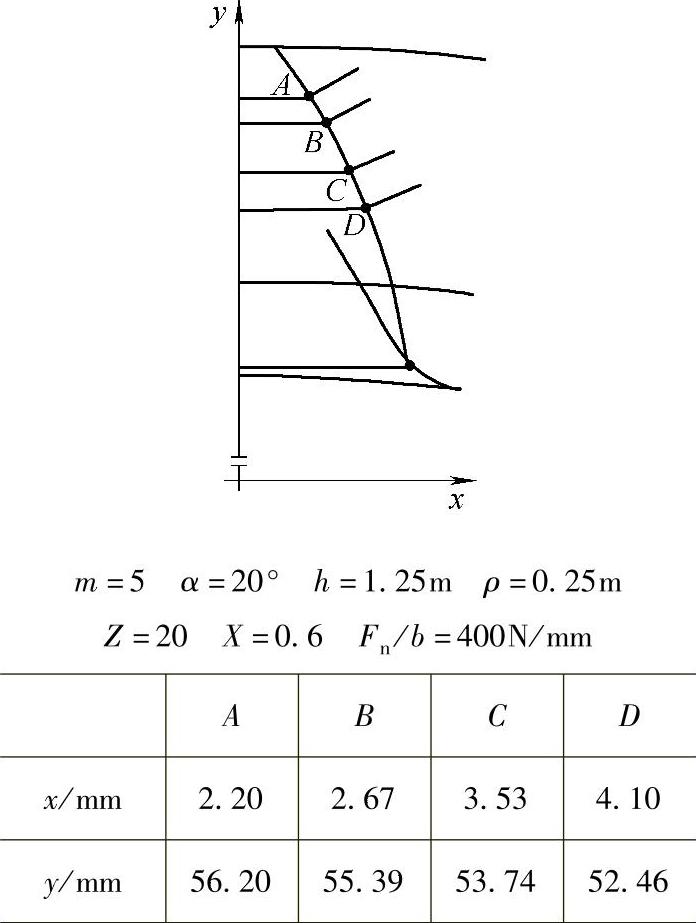
图3-22 共同齿形

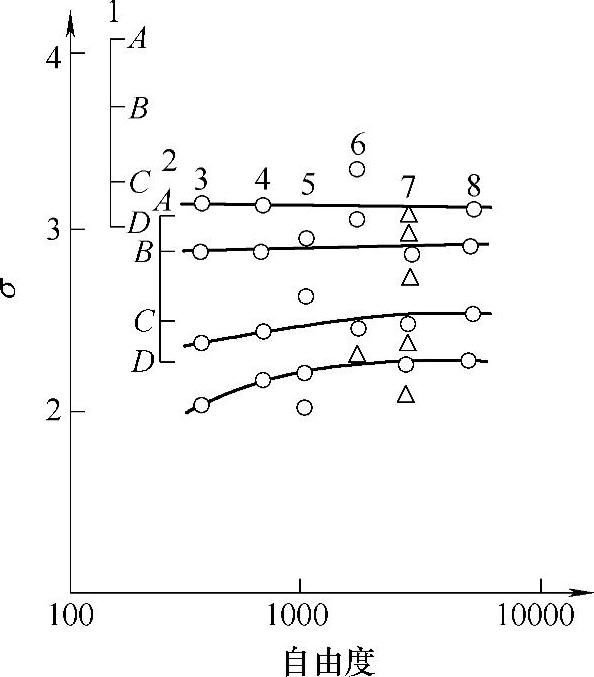
图3-23 齿根应力的计算结果

1—ISO1975年计算值 2—户部，天方映射函数 3—慕尼黑工大 4—户部，井上 5—弗利德利希司齿轮厂 6—MTU 7—达姆斯达特工大 8—Daimler-Benz公司

为了弄清单元型式对计算精度的影响，蒋孝煜对Chabert所计算的齿轮用三节点三角形单元也进行了计算。在计算之前先用本章2.1节所述方法确定齿廓坐标，过渡曲线部分按刀尖半径ρ=0.4m范成，然后分割成计算模型如图3-24所示，当载荷作用在齿顶上时，所得结果对比如下：

表3-3中Chabert的数据是根据其归纳的应力公式计算出来的。可以看出两种不同的单元形式所得的计算结果几乎相差无几。

表3-2 齿根应力的计算结果（F_a/b=400N/mm²）

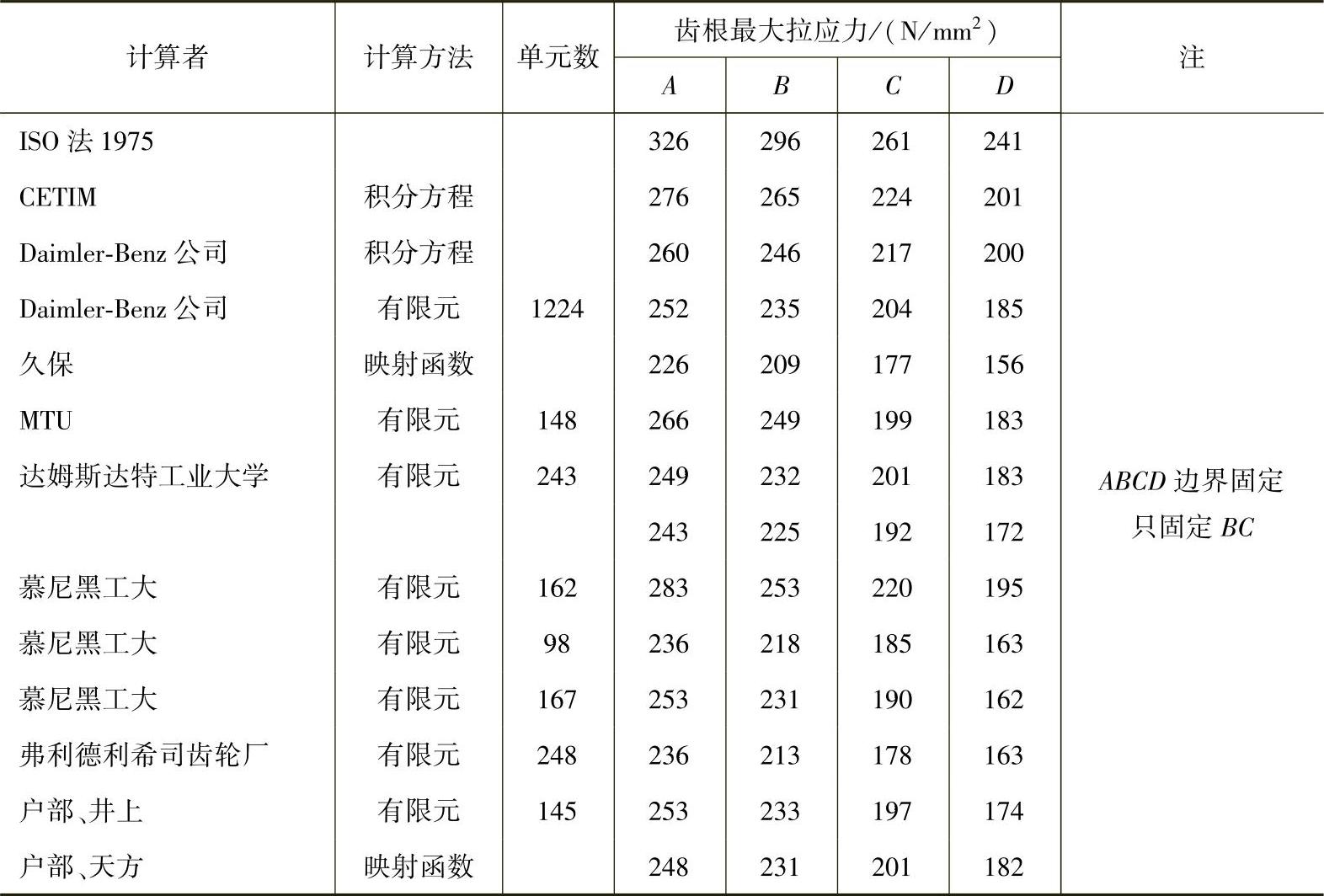
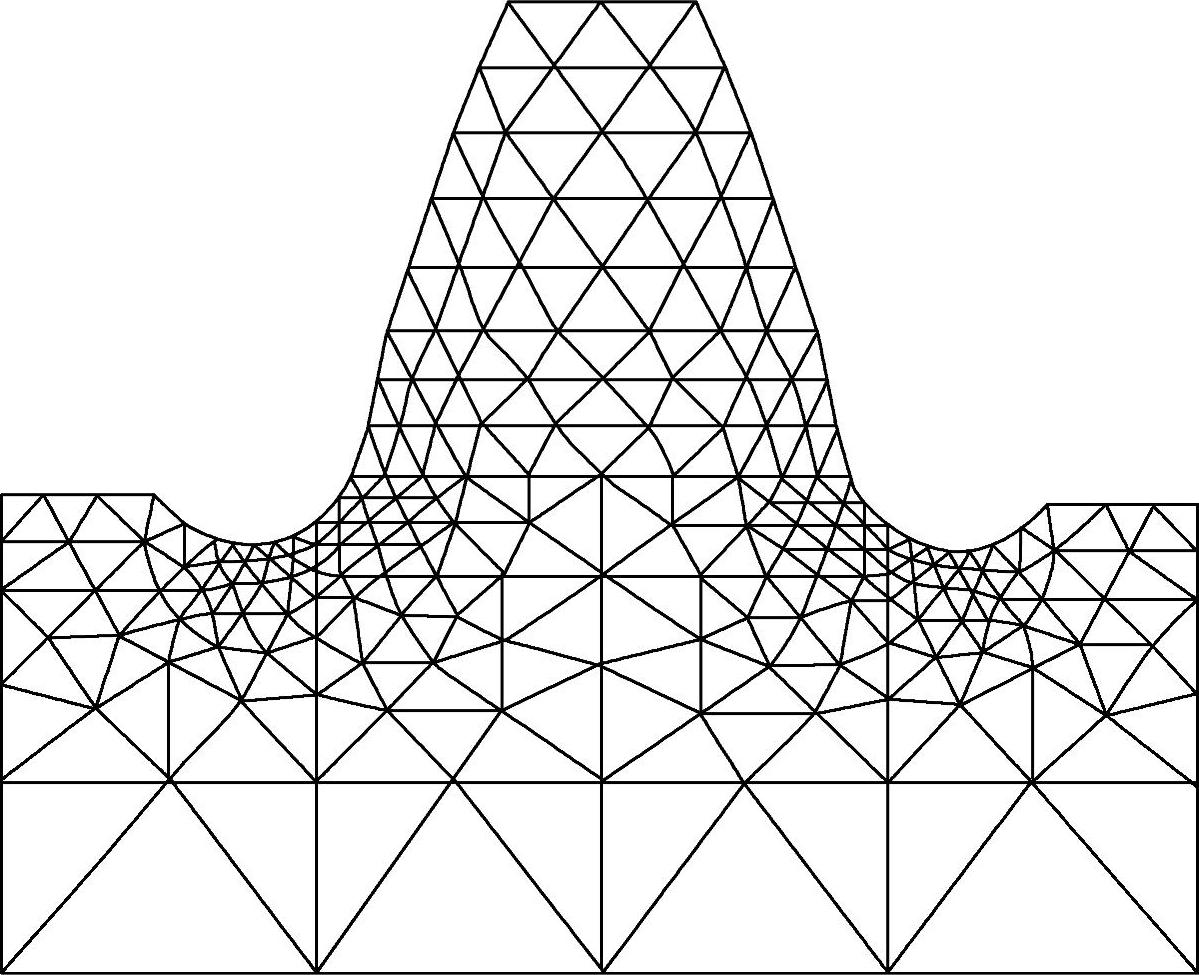
图3-24 计算模型

表3-3 齿根应力计算结果

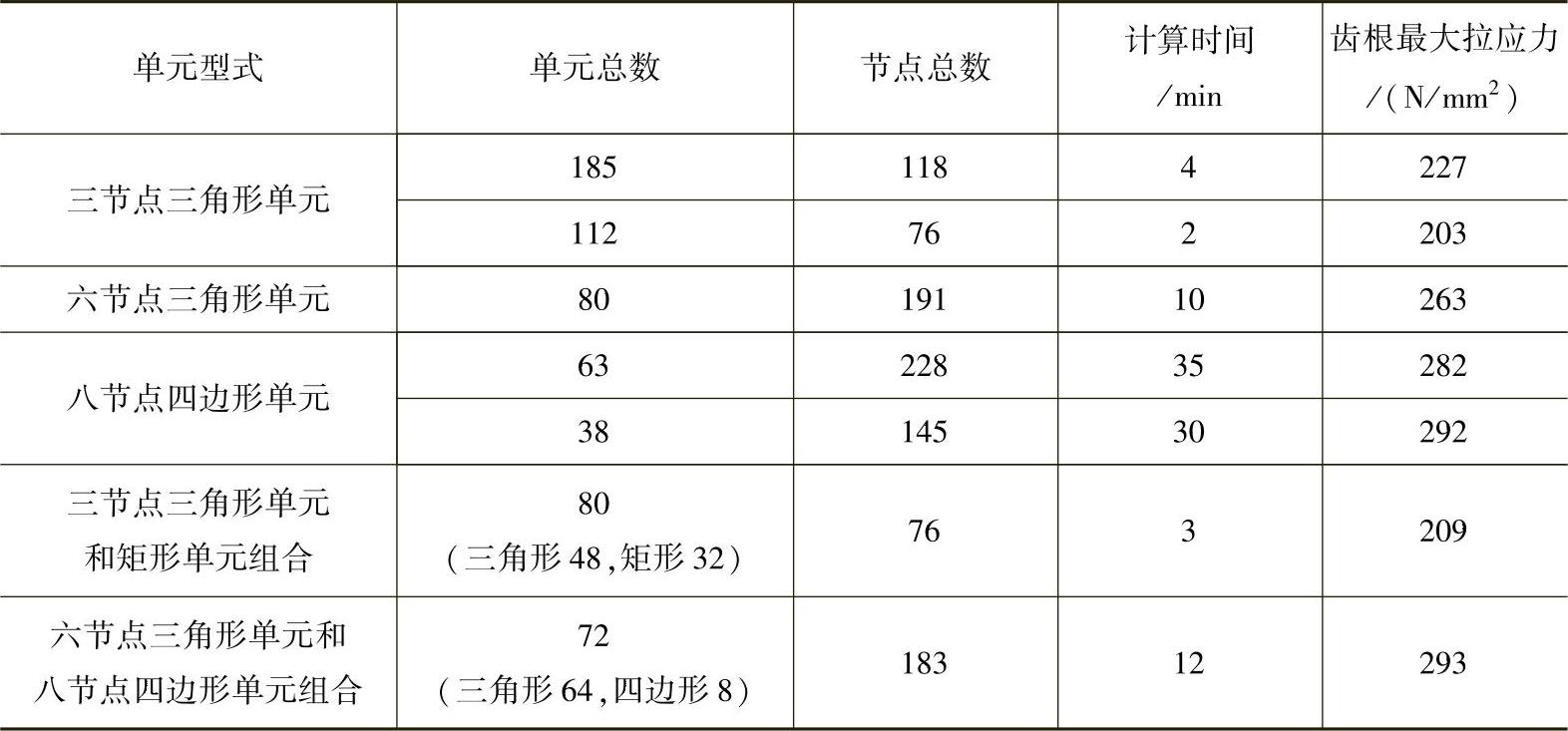
上海交通大学黄瑞清对同一齿轮用多种单元型式进行了计算，结果见表3-4。将表3-3中的单元数和表3-4中同类型的单元数相比较可知，表3-4中的两种三角形单元的单元数取得过少，所以应力计算值明显偏低。由表3-4也可以看出，若选用八节点四边形单元，则可用少量的单元而达到较高的精度，但计算时间则比其他单元要长许多。

表3-4 计算实例比较