行星齿轮传动的简化计算方法

由于行星齿轮传动采用功率分流，由数个行星轮承担载荷，同时采用合理的内啮合传动，与定轴传动相比具有许多突出的优点，其应用广泛。GB/T 19406—2003渐开线直齿和斜齿圆柱齿轮承载能力计算方法仅适用于校核计算，但在技术参数尚未确定时，是无法进行这一工作的。在行星齿轮传动设计时，将遇到同一情况。现介绍前苏联库德略采夫（B、H、КУДРЯВЦЕВ）计算方法，这种方法简明、实用，经大量的实践证明，是较符合我国国情的。

（1）转矩T₁的确定

1）在正确选择传动参数的条件下，对于常用的2K-H（NGW）型和2K-H（NW）型行星齿轮传动来说，其承载能力主要取决于外啮合。常采用提高齿面硬度和增大外啮合角（α_a′_g=22°～25°）的角度变位，以提高外啮合传动的承载能力。通常首先进行外啮合传动的强度计算，然后校核内啮合强度。

2）各种类型的行星齿轮传动，均可分解为相互啮合的几对齿轮副，对常用的2K-H型行星齿轮传动，其齿轮副的分解如图3-1所示。将啮合副中的小齿轮标为1，大齿轮标为2。因此，齿轮强度的计算可采用定轴齿轮的计算公式，如GB/T19406—2003或按库德略采夫的强度计算公式均可。但需要考虑行星齿轮传动的结构特点，即多行星轮和运行特点——行星轮既自转又公转。

行星齿轮传动齿轮副如下：NGW型可分解为a—g副和g—b副；NW型可分解为a—g副和f—b副；WW型可分解为a—g副和f—b副；锥齿轮传动分解为a—g副和g—b副（见图3-1）。

输入转矩T_a（N·m）（作用在太阳轮a上的转矩）

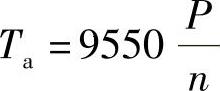
式中 P——电动机的输入功率（kW）；

n——输入转速（r/min）。

作用在小齿轮轮齿上的转矩T₁（N·m）（a—g副中）

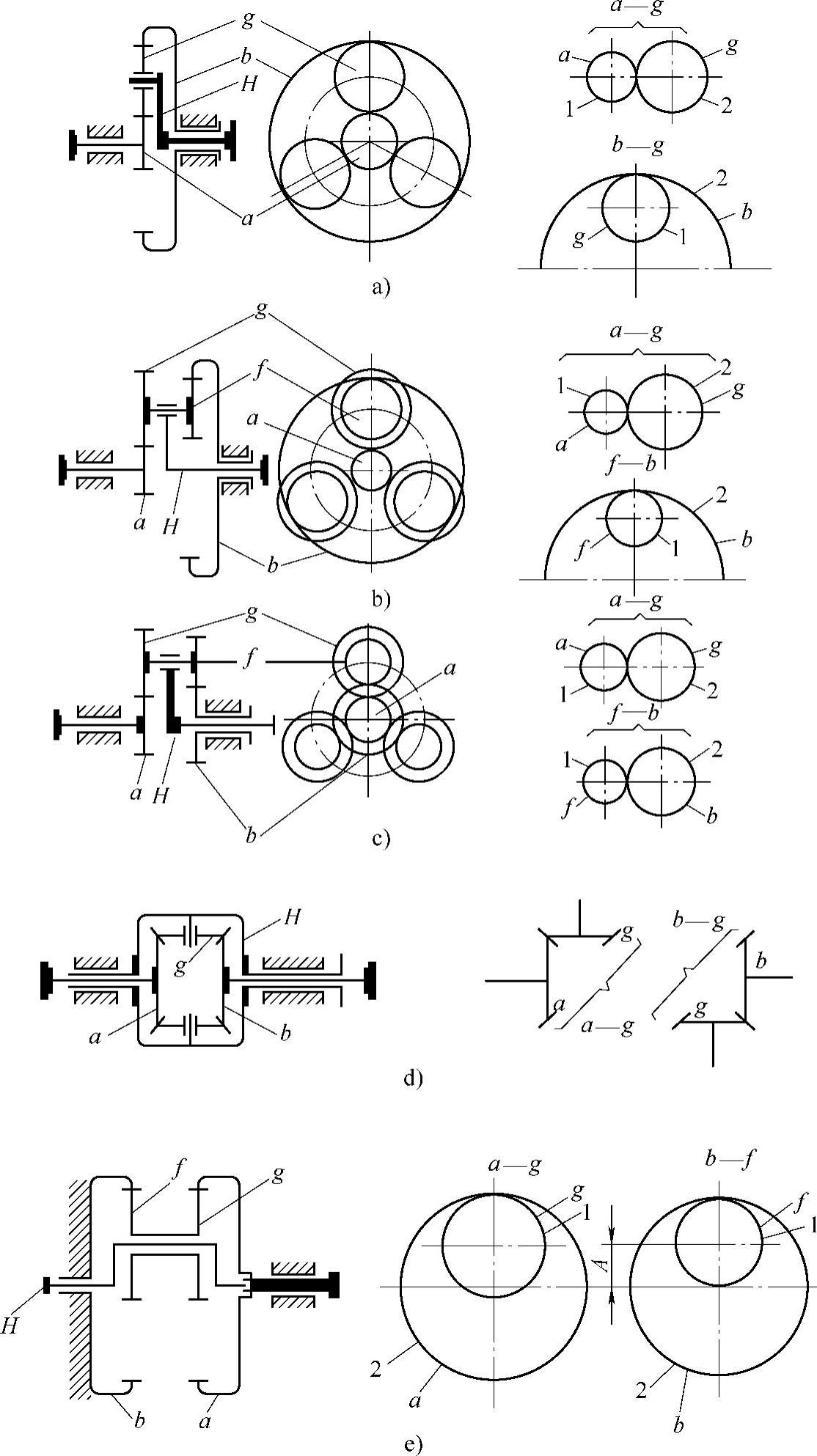
图3-1 行星齿轮传动强度计算时啮合副的分解

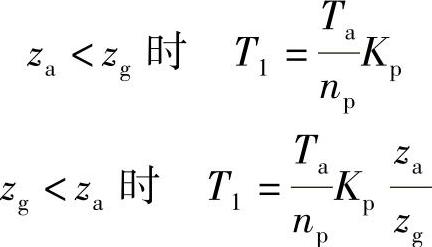
式中 n_p——行星轮的个数；

K_p——行星轮间载荷分配不均衡系数，对于具有基本元件浮动者，如太阳轮浮动或行星架浮动或内齿圈浮动或行星轮浮动，可取K_p=1.15，也可由计算或测试确定。

（2）强度计算 对于2K-H型行星齿轮传动，其承载能力主要取决于外啮合副（a—g），同时又是硬齿面，通常弯曲强度是主要矛盾。只要满足弯曲强度，齿面接触强度和内啮合副（b—g）的强度一般是较易通过校核计算的。

a—g副中的小齿轮强度计算，小齿轮1的分度圆直径d₁（mm）为

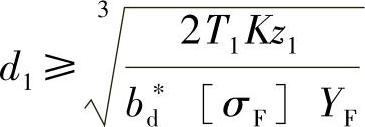
式中 z₁——a—g副中小齿轮的齿数；

K——载荷系数，取决于使用工况和过载能力，通常K=1.1～1.8，一般取K=1.2；

b_d^*——齿宽系数，通常取b_d*=0.5。当z_a≤z_g时，取b_d^*≤0.7，在z_a＞z_g时，

则b_d^*≤0.60，b_d^*=b/d₁；

Y_F——齿形系数，根据齿数z₁和变位系数x查图3-2选取；

[σ_F]——钢制齿轮的许用弯曲应力MPa，按表3-1计算确定。

（3）计算实例(www.xing528.com)

【例3-1】 已知一单级行星齿轮减速器，太阳轮齿数z_a=24，行星轮齿数z_g=25，内齿圈齿数z_b=75，行星轮个数n_p=3；采用太阳轮浮动，则载荷不均衡系数K_p=1.15；太阳轮、行星轮用20CrMnMo渗碳淬火，太阳轮齿面硬度56～60HRC，行星轮齿面硬度52～56HRC，内齿圈用42CrMo，齿坯调质处理，硬度255～285HBW；电动机为YZR280S-6，功率P=55kW，转速n=970r/min，传动比i^b_aH=1+z_b/z_a=1+75/24=4.125。试确定该减速器的主要参数。

解 ①确定小齿轮z₁（a—g副中的z_a）上的输入转矩T_a为

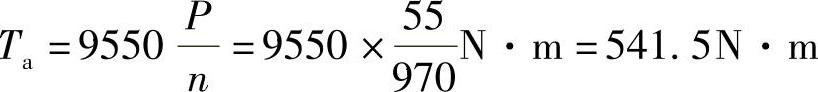
求出小齿轮z₁轮齿上的转矩T₁为

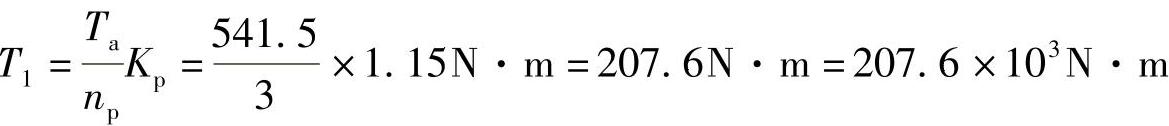
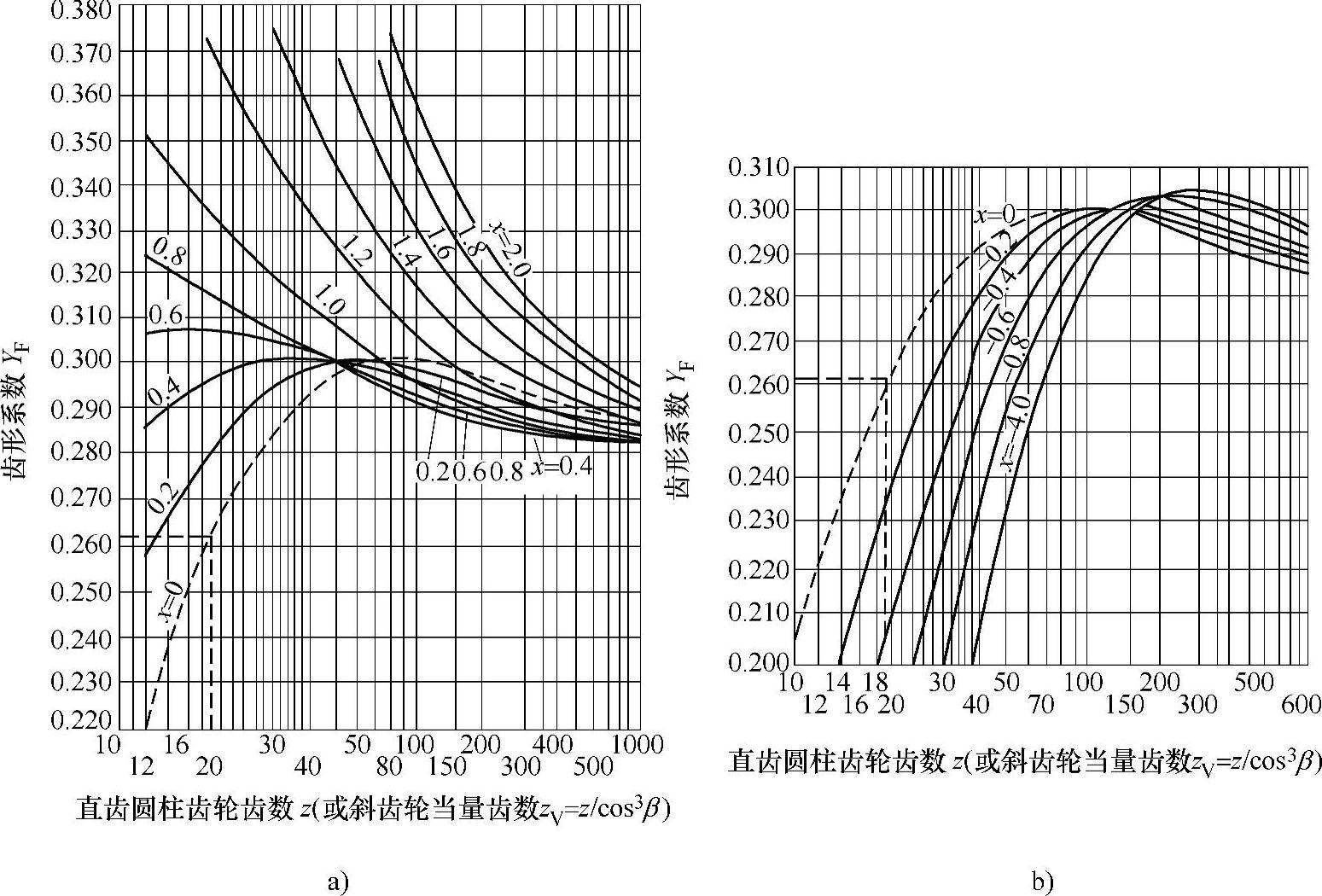
图3-2 确定外齿轮齿形系数Y_F的线图（α=20°，h_a^*=1）

a）变位系数x＞0 b）变位系数x<0

表3-1 钢制齿轮的许用弯曲应力[σ_F] （单位：MPa）

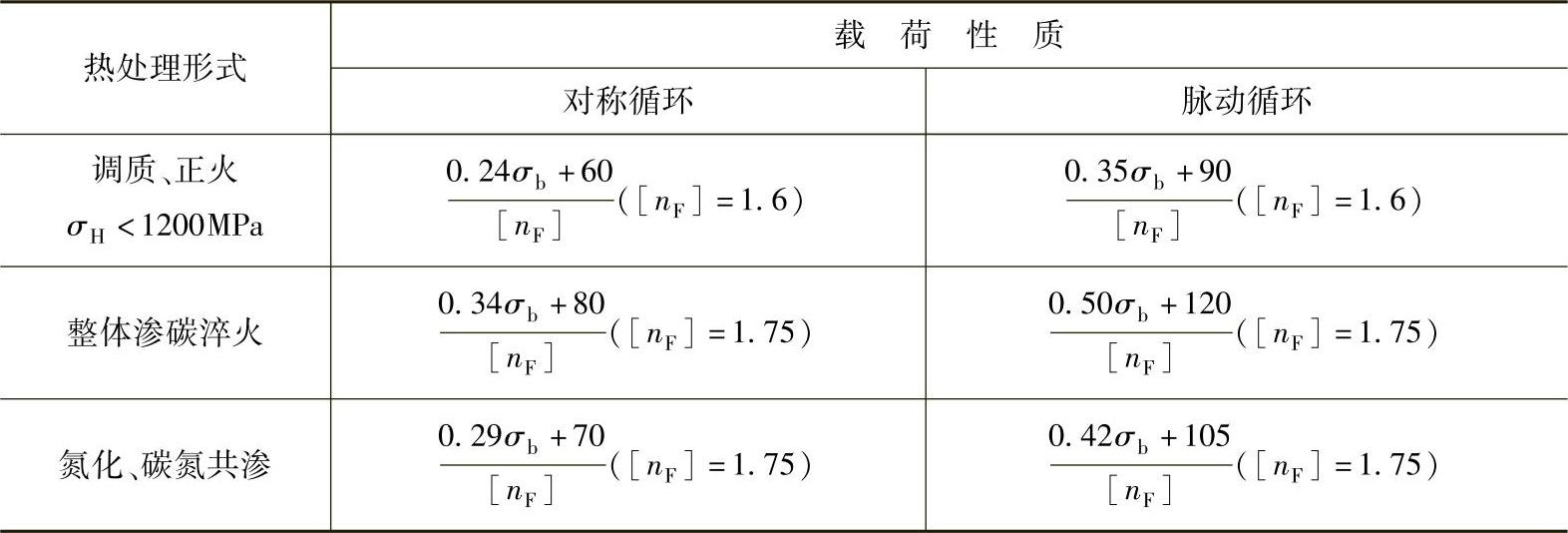
注：σ_H—齿面接触应力；σ_b—材料的强度极限；[n_F]—安全系数。

②小齿轮的分度圆直径d₁的确定

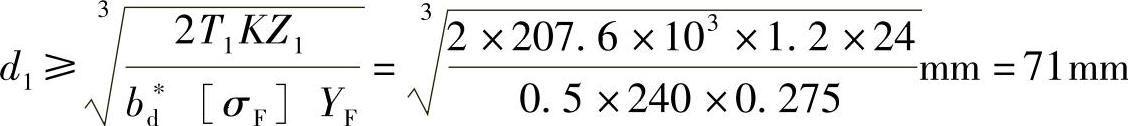
模数m=d₁/z₁=71/24=2.96，采用m=3。

齿宽系数b^*₁=b/d₁=0.5。

根据z₁=24，查图3-2，得齿形系数Y_F=0.275。

材料20CrMnMo，弯曲强度σ_b=1079MPa（截面尺寸δ=30mm时），则许用应力

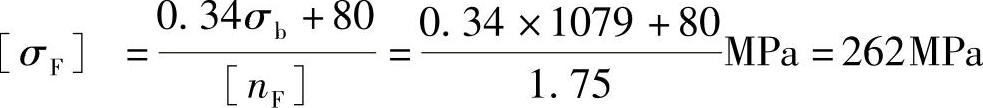
考虑到截面尺寸较大的影响，取[σ_F]=240MPa。

于是太阳轮分度圆直径d_a=mz_a=3×24mm=72mm。

行星轮分度圆直径d_g=mz_g=3×25mm=75mm。

内齿圈分度圆直径d_b=mz_b=3×75mm=225mm。

齿宽b=b_d^*d₁=0.5×72mm=36mm。

中心距a=75mm，太阳轮采用变位齿轮，变位系数x_a=0.538，其中齿顶高变动系数Δy=0.038。