计算单自由度振动的应力

（1）自由振动应力计算 以悬臂梁AB为例，如图2-8所示。梁振动时最大变形为

式中 δ_s——静变形；

a——振幅；

K_d——振动的动荷系数。

当振动变形较小，应力在弹性范围内时，振动应力σ_d为

σ_d=σ_sK_d （2-11）

式中，静应力σ_s是熟知的，所以振动应力计算的关键是动荷系数K_d，而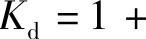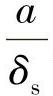，决定于对振幅a的计算。

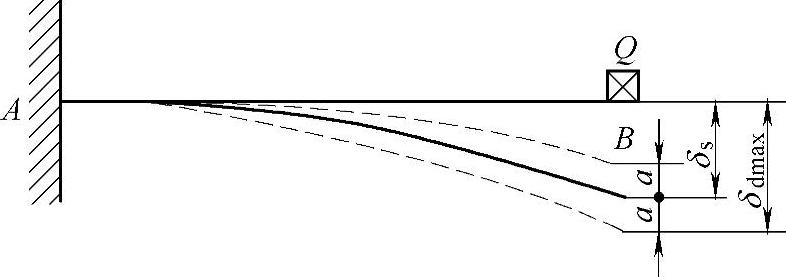
图2-8 单自由度振动示意图

单自由度振动方程为

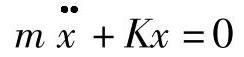
方程解的一般形式为

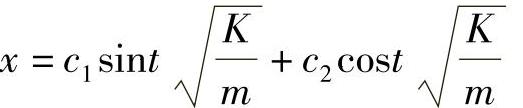
式中 c₁，c₂——积分常数，由重物运动的起始条件来决定。上式经适当变换可改写为谐振方程：

x=asin（Kt+α）

式中 a——振幅，。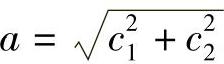

Kt+α——位相；

α——初位相。

a和α是两个常数，由运动的起始条件决定。假设初始时t=0，x=x₀，v=v₀，则由

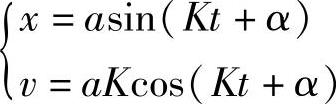
可得(https://www.xing528.com)

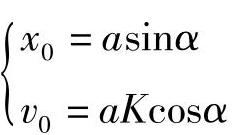
解出

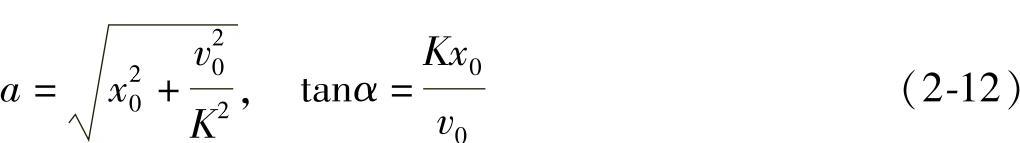
（2）阻尼受迫振动应力的计算 以简支梁为例，如图2-9所示。设梁上电动机重量为Q，角速度为ω，电动机转子偏心引起的离心惯性力为F，其垂直分量为Fsinωt，其水平分量一般略去不计，梁的自重与Q相比较小，可不考虑。

受迫振动的振幅为

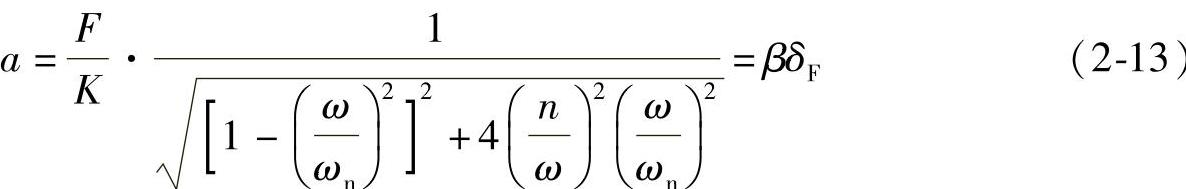
式中 K——梁的刚度（kg/cm或N/mm）；

ω——干扰力的频率（rad/s）；

ω_n——振动系统的固有频率（rad/s），

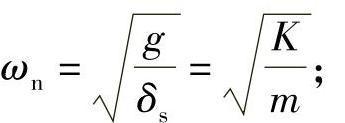
n——阻尼系数；

δ_F——最大干扰力F按静载荷作用于

梁上产生的变形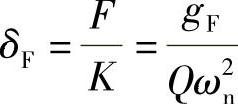，于是，动荷系数

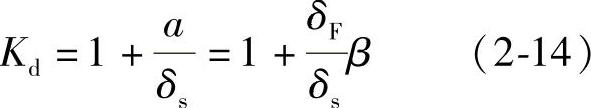
最大动应力

最小动应力

式中 β——增长系数，它与ω、ω_n、n有关，随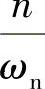及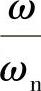的变化而变化。

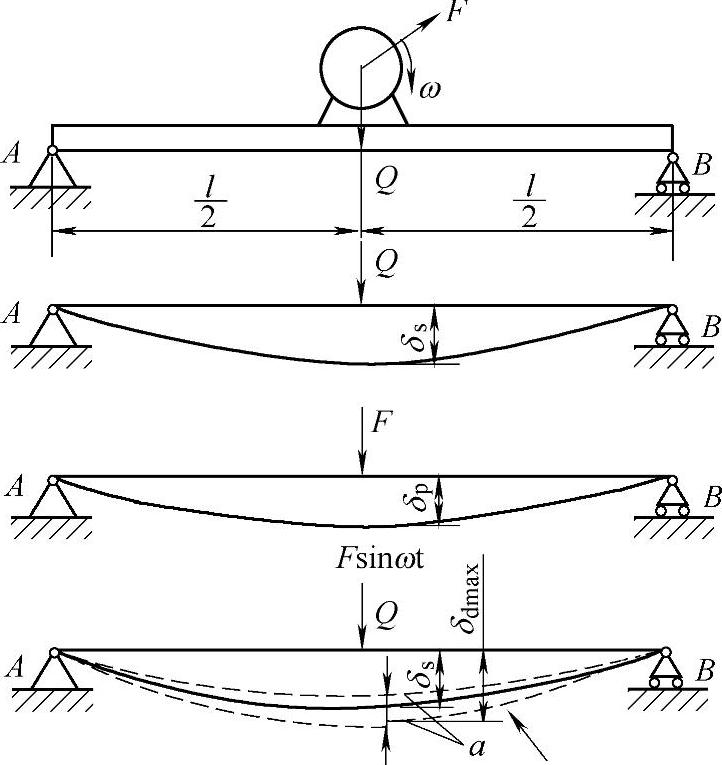
图2-9 简支梁受迫振动简图