【摘要】:并将确定的部分从总图中分离出来,经过简化绘出示意图,标注所有的外力,这就成了受力图。绘受力图的关键是简化要合理,既要符合零件的实际情况,又要便于计算、分析。常见的简化有以下几种:1)零件如有对称面,则可将对称分布的载荷和约束都简化到对称面内,作平面问题处理。表2-1 常见零件载荷的计算公式(续)(续)根据外力和约束情况,可求得所需截面的作用力。
实际零件的受力往往是复杂的,可能同时承受许多大小不等,方向不同的载荷作用,其分布状况也可能各不相同(分散、集中、对称、非对称,同一平面内、空间任意等),要逐一精确计算往往是困难的,也往往是没有必要的,必须根据具体问题的要求和精度指标,抓主要因素,忽略次要因素,尽量缩小研究的范围和具体对象。并将确定的部分从总图中分离出来,经过简化绘出示意图,标注所有的外力,这就成了受力图。
绘受力图的关键是简化要合理,既要符合零件的实际情况,又要便于计算、分析。常见的简化有以下几种:
1)零件如有对称面,则可将对称分布的载荷和约束都简化到对称面内,作平面问题处理。
2)若零件长度比横向尺寸大很多(一般大5~10倍),可简化为杆件处理。
截面变化不大的杆件可简化为共截面杆计算。
3)当载荷作用的范围的长度比零件的长度小很多时,可将分布力简化为集中力处理(但不能用于作用点附近的强度计算)。
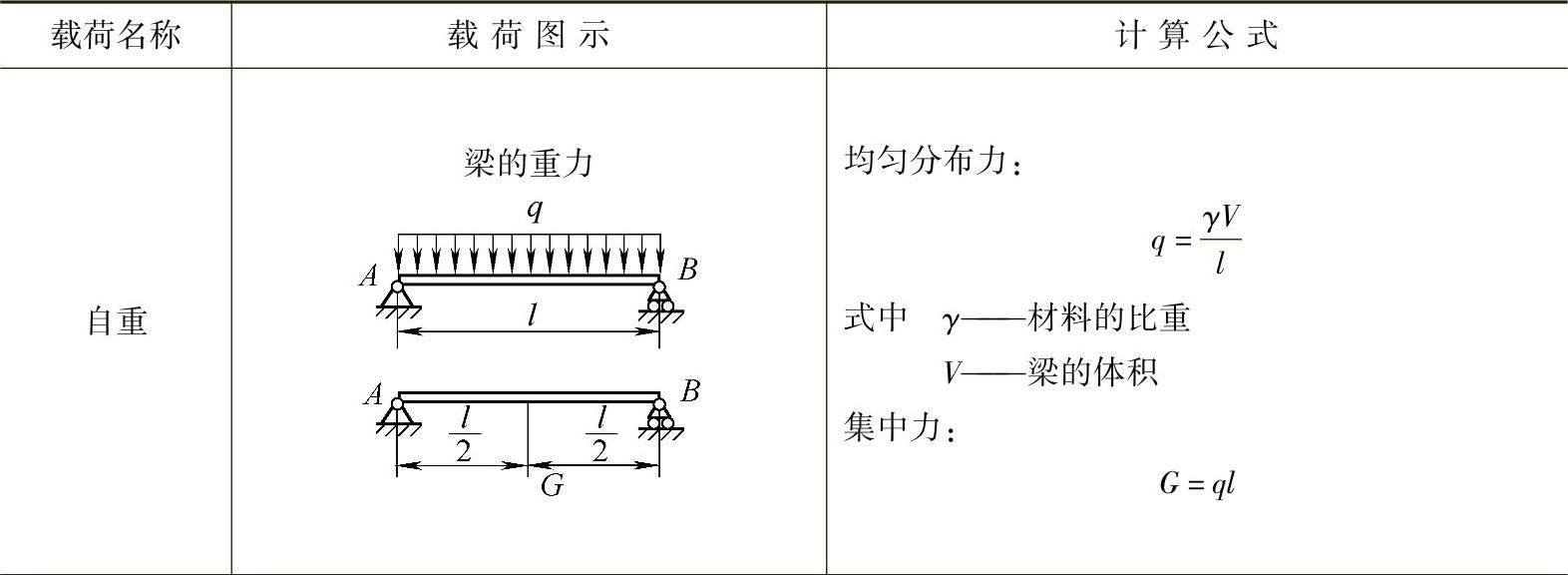
一般研究对象的主动力(载荷)由技术条件给出(或由功率折算)。但有些外力则需要分析、简化,采用相应公式计算。常见几种载荷计算公式如表2-1所列。
表2-1 常见零件载荷的计算公式(https://www.xing528.com)
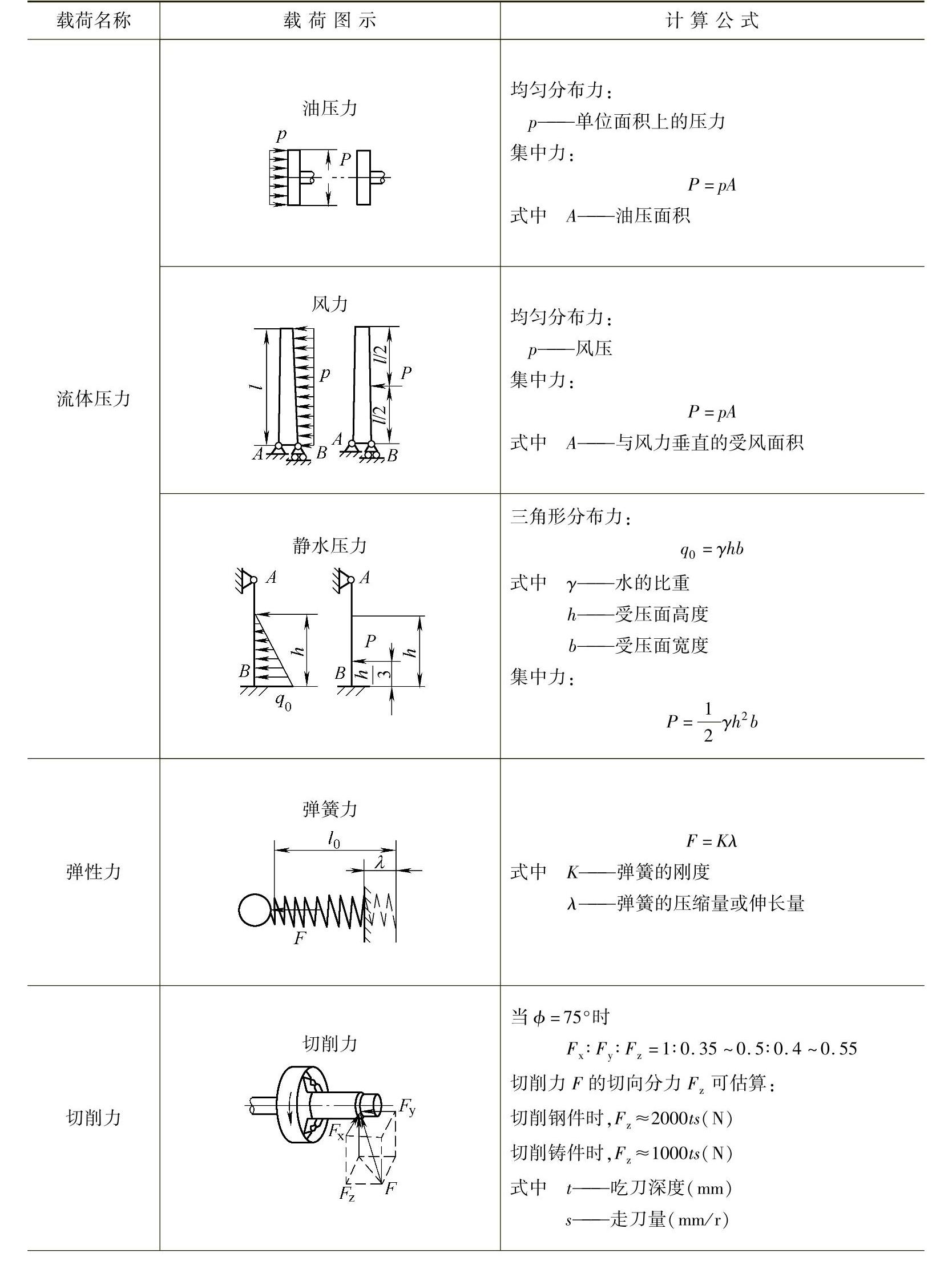
(续)
(续)
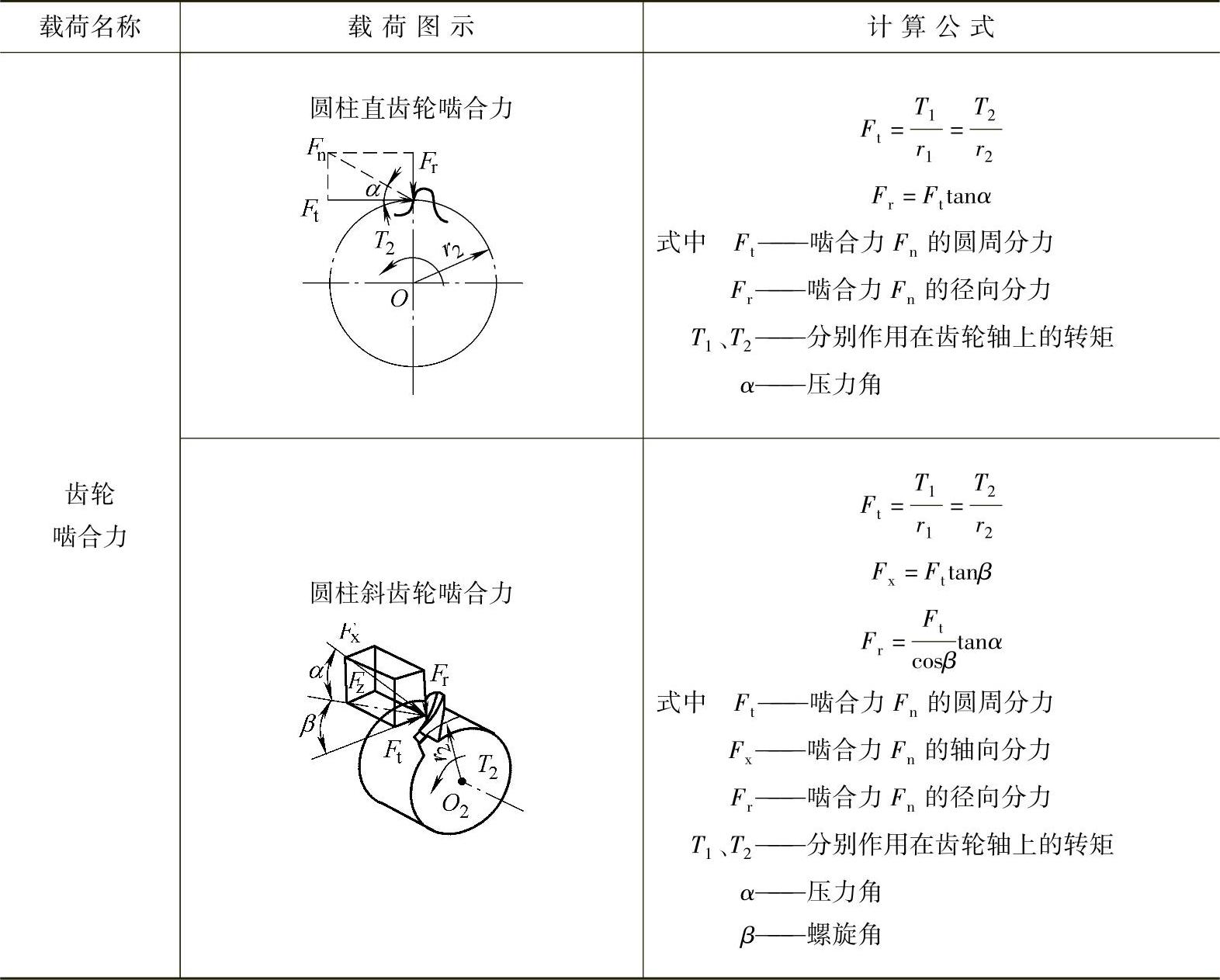
根据外力和约束情况,可求得所需截面的作用力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




