完全互换法（极值法）计算尺寸链的优化方法

从尺寸链各环的最大与最小极限尺寸出发进行尺寸链计算，不考虑各环实际尺寸的分布情况。按此法计算出来的尺寸加工各组成环，进行装配时各组成环不需挑选或辅助加工，装配后即能满足封闭环的公差要求，即可实现完全互换。

12.2.2.1　基本公式

设尺寸链的总环数为n，增环环数为m，A0为封闭环的公称尺寸，Az为增环的公称尺寸，Aj为减环的公称尺寸。

（1）公称尺寸的计算。

封闭环公称尺寸等于所有增环公称尺寸之和减去所有减环公称尺寸之和，即

式中，m为增环环数；n为总环数。

（2）极限尺寸的计算。

封闭环的最大极限尺寸等于增环最大极限尺寸之和减去减环最小极限尺寸之和；封闭环的最小极限尺寸等于增环最小极限尺寸之和减去减环最大极限尺寸之和，即

（3）极限偏差的计算。

封闭环的上偏差等于增环的上偏差之和减去减环的下偏差之和；封闭环的下偏差等于增环的下偏差之和减去减环的上偏差之和，即

（4）公差的计算。

封闭环公差等于各组成环公差之和，即

由式（12.8）可知，封闭环公差是该尺寸链中公差值最大的一环，即精度最低的一环。如要提高封闭环精度，可通过两个途径，一是缩小组成环公差；二是减少组成环环数。前者将使制造成本报高，因此，设计中往往从后者着手，应遵循“最短尺寸链”原则，即对某一封闭环，若存在多个尺寸链，则应选取组成环最少的那个尺寸链。可总结为：

①在尺寸链中封闭环的公差值最大，精度最低；

②在建立尺寸链时应遵循“最短尺寸链原则”，使组成环数目为最少。

12.2.2.2　例题

（1）正计算（校核计算）。

正计算用来求封闭环公称尺寸及偏差，其基本步骤是：根据装配要求确定封闭环；寻找组成环；画尺寸链线图；判别增环和减环；由各组成环的公称尺寸和极限偏差求封闭环公称尺寸和极限偏差。

【例12-1】　如图12.5（a）所示的结构，已知各零件的尺寸：A1＝ mm，A2＝A5＝ mm，A3＝ mm，A4＝mm，设计要求间隙A0为0.1～0.45 mm，试做校核计算。

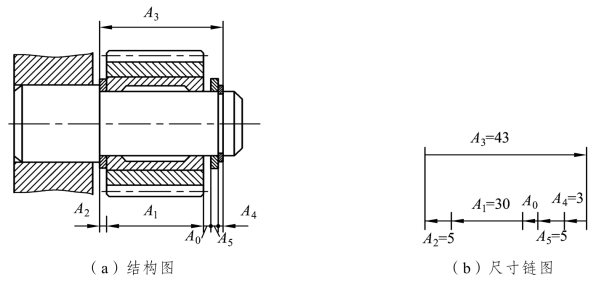
图12.5　齿轮部件尺寸链图

【解】（1）确定封闭环及其技术要求。

由于间隙A0是装配后自然形成的，所以确定封闭环为要求的间隙A0。此间隙在0.1～0.45 mm，即A0＝ mm。

（2）寻找全部组成环，画尺寸链图，并判断增、减环。

依据查找组成环的方法，找出全部组成环为A1、A2、A4和A5，如图12.5（b）所示。依据“回路法”判断出A3为增环，A1、A2、A4和A5都为减环。

（3）计算（校核）封闭环的公称尺寸。

A0=A3-(A1+A2+A4+A5)=43-(30+5+3+5)=0

封闭环的公称尺寸为0，说明各组成环的公称尺寸满足封闭环的设计要求。

（4）计算（校核）封闭环的极限偏差

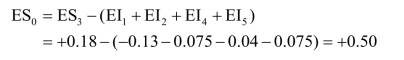
EI0=EI3-(ES1+ES2+ES4+ES5)=+0.02-(0+0+0+0)=+0.02

（5）计算（校核）封闭环的公差。

T0=T1+T2+T3+T4+T5=0.13+0.075+0.16+0.075+0.04=0.48

校核结果表明，封闭环的上、下偏差及公差均已超过规定范围，必须调整组成环的极限偏差。

②反计算（设计计算）。

在具体分配各组成环的公差时，可采用“等公差法”或“等精度法”。

当各组成环的公称尺寸相差不大时，可将封闭环的公差平均分配给各组成环。如果需要，可在此基础上进行必要的调整，这种方法叫“等公差法”。即组成环的平均公差为

所谓“等精度法”，就是各组成环公差等级相同，即各环公差等级系数相等（见表12.1）。设其值均为a，则

表12.1　公差等级系数a的值

按GB/T 1800.1—2020规定，在IT5～ITl8公差等级内，标准公差的计算式为 T=a·i，其中i为公差因子。在常用尺寸段内，公差因子可按式（12.11）计算，其值见表12.2。

计算出后，按标准查取与之相近的公差等级系数，进而查表确定各组成环的公差。(www.xing528.com)

表12.2　公差因子i的值

各组成环的极限偏差确定方法是：先留一个组成环作为调整环，其余各组成环的极限偏差按“入体原则”确定，即包容尺寸的基本偏差为H，被包容尺寸的基本偏差为h，一般长度尺寸用js。进行公差设计计算时，最后必须进行校核，以保证设计的正确性。

【例12-2】如图12.5所示的装配结构，已知各零件的公称尺寸为：A1＝30 mm，A2＝A5＝5 mm，A3＝43 mm，弹簧卡环A4＝ mm（标准件），设计要求间隙A0为0.1～0.35 mm，试用“等精度法”确定各有关零件的轴向尺寸的公差和极限偏差。

【解】①确定封闭环及其技术要求。

由于间隙A0是装配后自然形成的，所以确定封闭环为要求的间隙A0。此间隙在0.1～0.35 mm，即A0= mm。封闭环的公差为

T0=ES0+EI0=+0.35-(+0.10)=0.25 mm

②寻找全部组成环，画尺寸链图，并判断增、减环。

依据查找组成环的方法，找出全部组成环为A1、A2、A3、A4和A5，如图12.5所示。依据“回路法”判断出A3为增环，A1、A2、A4和A5都为减环。

③校核封闭环的公称尺寸。

计算（校核）封闭环的公称尺寸为

A0=A3-(A1+A2+A4+A5)=43-(30+5+3+5)=0

封闭环的公称尺寸为0，说明各组成环的公称尺寸满足封闭环的设计要求。

④计算各组成环的公差。

由表12.2可查各组成环的公差因子值（单位为μm），即

i1=1.31；i2=i5=0.73；i3=1.56

得各组成环相同的公差等级系数

由表12.1知，aav=46，在TI9和IT10之间，因要保证不超出，故选取公差等级为IT9。查表2.1得各组成环的公差为

T1=0.052 mm，T2=T5=0.030 mm

T3=0.062 mm，T4=0.050 mm（已知）

⑤校核封闭环公差。

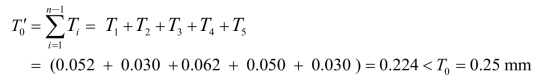
T3=（0.25-0.224+0.062)=0.088 mm

符合要求，还有富余。因此，可考虑放大较难加工的A3的公差。

⑥确定各组成环的极限偏差。

选A3作为调整环，其余根据“入体原则”，由于除A3外，其余均为被包容尺寸，故取其上偏差为零，即 A1=，A2=A5=，A4=（已知）。

得调整环A3的极限偏差

ES0=ES3-(EI1+EI2+EI4+EI5)

0.35=ES3-(-0.052-0.030-0.050-0.030)

ES3=+0.188mm

EI0=EI3-(ES1+ES2+ES4+ES5)

0.10=EI3-(0+0+0+0)

EI3=+0.10mm

因此，A3= mm。

（3）中间计算。

中间计算常用在基准换算和工序尺寸换算等工艺计算中。零件加工过程中，选定的定位基准或测量基准与设计基准不重合，则应根据工艺要求改变零件图的标注，此时需要进行基准换算，求出加工所需要的工序尺寸。

【例12-3】如图12.6所示的套筒零件，设计尺寸如图中所标，加工时，测量尺寸 较为困难，而用深度游标卡尺直接测量大孔的深度则方便，则成为间接保证的封闭环A0，A1为增环，A2为减环。为了间接保证A0，须进行尺寸换算，确定A2尺寸及其偏差。

图12.6　套筒零件尺寸链

【解】确定封闭环为A0，寻找组成环并画出尺寸链图，判断A1为增环，A2为减环。

因为　A0=A1-A2

所以　A2=A1-A0=50-10=40

因为　ES0=ES1-EI2，EI0=EI1-ES2

所以　EI2=ES1-ES0=0

ES2=EI1-EI0=-0.17-(-0.36)=+0.19mm

即组成环 A2的尺寸为 。

完全互换是从尺寸的极限情况出发解决问题，计算简单，但环数不能过多，精度也不能太高，否则会造成各组成环的公差过小，使加工困难，经济性不好。由于在成批生产中零件的尺寸常常是符合正态分布的，所以在尺寸链环数较多、精度较高时，尽量用大数互换法求解。