普通螺纹几何参数对互换性的影响

7.1.3.1　普通螺纹的几何参数

圆柱螺纹连接是由圆柱外螺纹旋入圆柱内螺纹而构成的。

按《普通螺纹 基本牙型》（GB/T 192—2003）规定，普通螺纹的基本牙型如图7.1所示。螺纹的几何参数取决于螺纹轴向剖面内的基本牙型，其基本牙型是将原始三角形（等边三角形）的顶部截去H/8和底部截去H/4所形成的内、外螺纹共有的理论牙型。该牙型具有螺纹的基本尺寸（小写字母为外螺纹的几何参数，大写字母为内螺纹的几何参数）。螺纹的主要参数有：

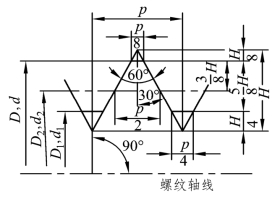
图7.1　普通螺纹的基本牙型和基本尺寸

（1）大径（D，d）。

大径是指与内螺纹牙底或外螺纹牙顶相切的假想圆柱的直径。相结合的内、外螺纹的大径基本尺寸相等，即D＝d。国家标准规定，普通螺纹大径的基本尺寸为螺纹公称直径尺寸。

（2）小径（D1，d1）。

小径是指与内螺纹牙顶或外螺纹牙底相切的假想圆柱的直径。相结合的内、外螺纹的小径基本尺寸相等，即D1＝d1。

与牙顶相切的假想圆柱的直径通常又称为顶径，即内螺纹的小径和外螺纹的大径；与牙底相切的假想圆柱的直径又称为底径，即内螺纹的大径和外螺纹的小径。

（3）中径（D2，d2）。

中径是指一个假想圆柱的直径，该圆柱的母线通过螺纹牙型上沟槽和凸起宽度相等的地方。该假想圆柱称为中径圆柱。相结合的普通螺纹，内外螺纹的中径公称尺寸是相等的，并且与大径（D，d）和原始三角形高度（H）之间有下列关系：

注意：普通螺纹的中径不是大径和小径的平均值。

（4）螺距（P）与导程（Pn）。

螺距是指相邻两牙在中径线上对应两点间的轴向距离。导程是指在同一条螺旋线上相邻两牙在中径线上对应两点间的轴向距离。对单线（头）螺纹，导程等于螺距；对多线（头）螺纹，导程等于螺距与线数（n）的乘积：Pn＝P×n。

（5）单一中径（D2s，d2s）。

单一中径是指一个假想圆柱的直径，该圆柱的母线通过牙型上沟槽宽度与螺距基本尺寸的一半相等的地方。当螺距没有误差时，螺纹的中径就是螺纹的单一中径。当螺距有误差时，螺纹的单一中径与中径是不相等的。

（6）牙型角（α）与牙型半角（α/2）。

牙型角是指在螺纹牙型上，两相邻牙侧间的夹角，对于公制普通螺纹，牙型角α＝60°

牙型半角是指在螺纹牙型上牙侧与螺纹轴线的垂直线间的夹角。普通螺纹的牙型半角为α/2＝30°。

（7）螺纹升角（φ）。

螺纹升角是指在中径圆柱上螺旋线的切线与垂直于螺纹轴线的平面之间的夹角。螺纹升角与螺距和中径之间的关系有：

（8）螺纹旋合长度（L）：

螺纹旋合长度是指两个相互配合的螺纹沿螺纹轴线方向彼此旋合部分的长度。

部分普通螺纹的公称直径系列及主要几何参数的基本尺寸见表7.1。

表7.1　部分普通螺纹的基本尺寸　mm

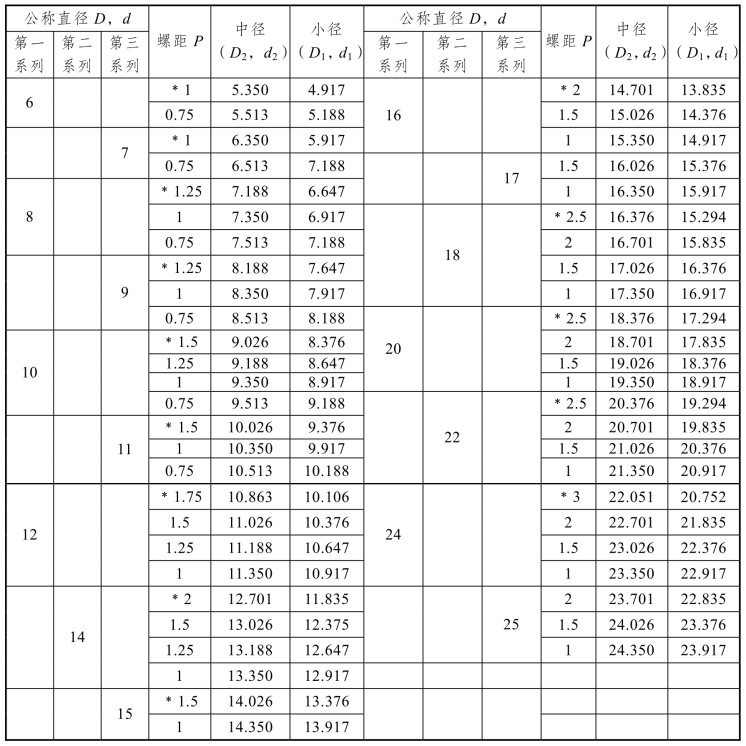
注：①直径优先选用第一系列，其次是第二系列，尽可能不用第三系列。
②用*标明的螺距为粗牙。

7.1.3.2　影响普通螺纹连接精度的因素

对普通螺纹互换性的主要要求是可旋合性和连接的可靠性（有足够的接触面积，从而保证一定的连接强度）。由于螺纹的大径和小径处均留有一定的间隙，一般不会影响其配合性质。而内外螺纹连接就是依靠它们旋合以后牙侧接触的均匀性来实现的。因此，影响螺纹精度的主要几何参数有螺距、牙型半角和中径。

（1）螺距误差的影响。

对于普通螺纹，螺距误差会影响螺纹的旋合性和连接强度。

螺距误差包括单个螺距误差和螺距累积误差。单个螺距误差也称为局部误差，是指单个螺距的实际尺寸与其基本尺寸之代数差，与旋合长度无关；螺距累积误差是指旋合长度内，任意个螺距的实际尺寸与其基本尺寸之代数差，与旋合长度有关。其中累积误差对螺纹互换性的影响更为明显，为保证可旋合性，必须对旋合长度范围内的任意两螺牙间螺距的最大累积偏差加以控制。螺距累积误差对互换性的影响如图7.2所示。

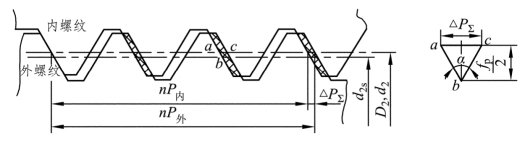
图7.2　螺距累积误差对互换性的影响

假设内螺纹具有理想的牙型，外螺纹的中径及牙型半角与内螺纹的相同，但外螺纹的螺距有误差，并假设外螺纹的螺距比内螺纹的螺距大。假定n个螺牙长度上，螺距累积误差为ΔP∑。从图7.2中可以看出，内外螺纹的牙型将产生干涉，使得外螺纹不能自由旋入内螺纹。为了使有螺距误差的外螺纹仍能自由旋入标准的内螺纹，在制造时可把外螺纹的中径减小一个数值fp（当内螺纹的螺距有误差时，可把内螺纹的中径加大一个数值），这个fp就是补偿螺距误差的影响而折算到中径上的数值，被称为螺距误差中径当量。

从图7.2可知

对于牙型角α＝60°的普通螺纹，则有(www.xing528.com)

fp＝1.732|ΔP∑|

式中的ΔP∑之所以取绝对值，是由于ΔP∑不论是正值还是负值，影响旋合性的性质不变，只是改变了牙侧干涉的位置。ΔP∑应是旋合长度上最大的螺距累积误差，而该值并不一定就出现在最大旋合长度上。

（2）牙型半角误差的影响。

牙型半角误差是指牙型半角的实际值与公称值的代数差，是螺纹牙侧相对于螺纹轴线的位置误差。对螺纹的旋合性和连接强度均有影响。

为了便于分析，假设内螺纹具有理想的牙型，外螺纹的中径及螺距与内螺纹的相同，而且都没有误差，仅外螺纹的牙型半角有误差，这样内外螺纹旋合时牙侧将产生干涉，如图7.3所示。

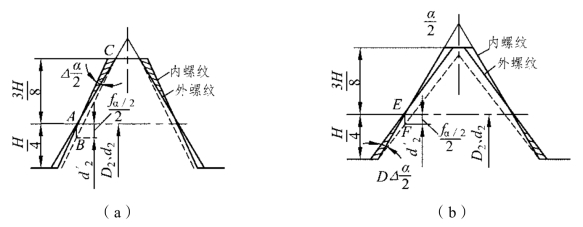
图7.3　牙型半角误差对螺纹互换性的影响

图7.3（a）所示为外螺纹的牙型半角小于内螺纹的牙型半角，其牙顶部分的牙侧有干涉现象；图7.3（b）所示为外螺纹的牙型半角大于内螺纹的牙型半角，其牙根部分的牙侧有干涉现象。为了消除干涉，使内外螺纹能旋合，可将牙型半角误差转变成中径当量fα/2，即把具有牙型半角误差的外螺纹的中径减小fα/2（当内螺纹的牙型半角有误差时，把内螺纹的实际中径增加fα/2）。

根据任意三角形的正弦定理，考虑到左右牙型半角误差可能同时出现的各种情况及必要的单位换算，可推得通式如下

式中：fα/2为牙型半角误差的中径当量（μm）；P为螺距（mm）；为左、右牙型半角误差（′）；K1、K2为左、右牙型半角误差系数。对外螺纹，当牙型半角误差为正时，K1和K2取2；为负时，取为3。对内螺纹，当牙型半角误差为正时，K1和K2取3；为负时，取为2。

（3）中径误差的影响。

螺纹中径误差是指中径实际尺寸与基本中径的代数差。内外螺纹相互作用集中在牙型侧面，内外螺纹中径的差异直接影响牙型侧面的接触状态，从而对螺纹的旋合性和连接强度产生影响。

假设其他参数处于理想状态，外螺纹的中径小于内螺纹的中径，就能保证内外螺纹的旋合性；反之，就会产生干涉而难以旋合。但是，如果外螺纹的中径过小，内螺纹的中径过大，则会削弱螺纹的连接强度。为此，加工螺纹时应当对中径误差加以控制。

（4）螺纹作用中径及螺纹中径合格性的判断原则。

① 作用中径。实际上，螺距误差、牙型半角误差和中径误差是同时存在的。为了保证螺纹的旋合性，外螺纹只能与一个中径较大的内螺纹旋合，其效果相当于外螺纹的中径增大，这个增大了的假想中径称为外螺纹的作用中径（d2作用），它是与内螺纹旋合时起作用的中径；对于内螺纹只能与一个中径较小的外螺纹旋合，其效果相当于内螺纹的中径减小了，这个减小了的假想中径称为内螺纹的作用中径（D2作用）。即有

外螺纹的作用中径d2作用：

内螺纹的作用中径D2作用：

作用中径是在规定的旋合长度内，正好包容实际螺纹的一个假想的理想螺纹的中径，这个假想螺纹具有基本牙型的螺距、半角和牙型高度，并在牙顶和牙底留有间隙，以保证不与实际螺纹的大小径发生干涉。螺纹的作用中径如图7.4所示。

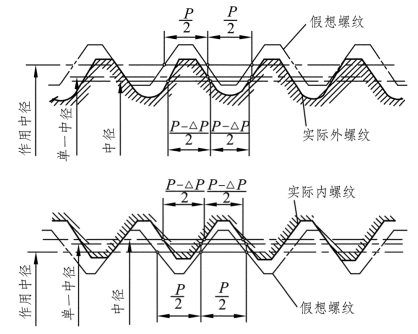
图7.4　螺纹的作用中径

螺纹的实际中径D2实际（d2实际）用其单一中径代替。

因为螺纹的螺距误差和半角误差均可折算成中径当量，即折算成中径误差的一部分，因此，国家标准没有单独规定螺距和牙型半角公差，只规定了中径公差（TD2、Td2），这个公差同时控制实际中径（单一中径）误差、螺距误差和牙型半角误差的共同影响。

②螺纹中径合格性的判断原则。螺纹中径合格性的判断原则遵循泰勒原则：实际螺纹的作用中径不允许超出最大实体牙型的中径，而实际螺纹上任何部位的实际中径（单一中径）不允许超出最小实体牙型的中径。

对于外螺纹，最大实体牙型的中径就是该螺纹中径的上极限尺寸，最小实体牙型的中径就是该螺纹中径的下极限尺寸。

对于内螺纹，最大实体牙型的中径就是该螺纹中径的下极限尺寸，最小实体牙型的中径就是该螺纹中径的上极限尺寸。

所以螺纹中径合格性的判断条件就是

对于外螺纹：d2作用≤d2max，d2单一≥d2min；

对于内螺纹：D2作用≥D2min，D2单一≤D2max。

【例7-1】螺纹误差计算举例。

某螺纹公称直径D为20 mm，螺距P为2.5 mm，公差带为7H，测得实际中径D2实际＝18.61 mm，螺距累积误差 ΔP∑=40μm，实际牙型半角为α1/2＝30°30′，α2/2＝29°10′，请判断此螺纹的中径是否合格？

【解】查表可知螺纹中径的公称尺寸为18.376mm，下偏差为0，公差为0.280mm，所以螺纹中径的尺寸范围为18.376～18.656 mm。

螺距累积误差的中径当量为 fp==0.069mm；

牙型半角误差的中径当量为 fα/2==0.035mm；

作用中径为 D2作用=D2实际-（fP+fα/2）=18.506mm；

因为 D2作用=18.506mm＞D2min=18.376mm

D2实际=18.61mm＜D2max=18.506mm

所以，此螺纹中径合格。