单根无损线路的Bergeron等值计算方法

Bergeron特征线计算方法是利用线路上波过程的特征线方程,经过一定的转换,把分布参数的线段等值为电阻性网络,再运用求解电阻性网络的通用方法计算整个网络的暂态过程。因此在暂态计算以前先要把分布参数线路中,储能的集中参数元件L、C等值为电阻性的计算电路。在此主要讨论单相无损线的Bergeron等值计算电路和相应的等值计算公式。

在数值求解网络暂态过程时,从计算开始时刻t 0起,把时间离散成一系列较小的时间间隔,一般采用等时间步长Δt,即t 1=t 0+Δt,t 2=t 0+2Δt,…,t n=t 0+nΔt共计算n步。在计算t时刻网络状态时,假定t时刻以前的状态作为历史记录是已知的。这样就可以逐点计算出网络中节点电压、支路电流或其他电量随时间变化的规律和波形。

在讨论运用特征线方法数值求解线路波过程之前,先扼要介绍一下特征线方法的基本原理。

1.特征线性方法的基本原理

分布参数线路上任何一点的对地电压和导线中的电流是距离x和时间t的函数,是电磁波沿线路传播的过程。若先考虑到线路单位长度的电阻R 0、电感L 0、电导G 0和电容C 0均为常数,和频率无关,则单导线线路上的波过程可以用以下的偏微分方程来描述

若略去损耗,则可以有如下的无损线的偏微分方程

对方程(4-2)进行合并,可以得到以下的波动方程,是二阶偏微分方程,即

其中

式中:v为流动波沿线的传播速度,对于无损架空线路来说其等于光速v 0,即电磁波在真空中的传播速度。

2.单根无损线路的Bergeron等值计算

以上单根无损线波动方程的电压和电流解可以写成以下形式

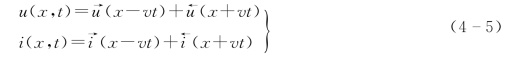
其中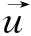和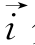分别表示以速度为v沿着x正方向传播的前行电压波和电流波,而和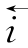表示沿x反方向传播的反行电压波和电流波。前行电压波和前行电流波之间,以及反行电压波和反行电流波之间是通过波阻抗相联系的。

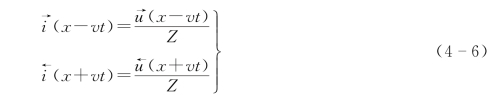
若将式(4-6)代入式(4-5),分别消去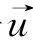或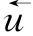就可以得到以下前行特征方程和反行特征方程

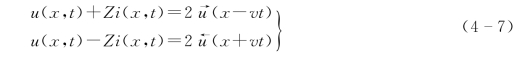
以上两个特征方程的物理意义可以描述如下:

方程式中u(x,t)和i(x,t)分别表示在线路上x点在t时刻的电压和电流的瞬时值,根据式(4-5),它们是前行波和反行波的叠加。

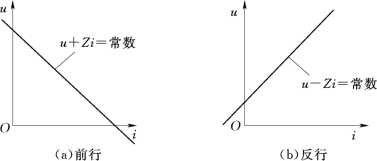
图4-20　前行和反行特征线

对前行波来说,若取x-vt=常数,则2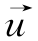(x-vt)值不变,从前行特征方程式(4-7)看,这意味着u(x,t)+Zi(x,t)的计算值不变。其物理意义为:因为线路均匀无损,所以电磁波沿线路向前传播时不发生畸变和衰减,当观察者沿x正方向以速度v和前行波一起运动时(即x-vt=常数),则根据它所处的位置x在i时刻观察到的瞬时电压值u(x,t)和电流值i(x,t)所计算得到的u(x,t)+Zi(x,t)值始终保持不变,等于两倍前行电压波的大小。这种情况从线路始端(x=0)一直到末端(x=l)都成立。

前行特征方程式(4-7)可用图4-20(a)所示的前行特征线表示。前行特性线在u-i坐标中是斜率为-Z的直线,它的位置需要由边界条件和起始条件来决定。一般可以由观察者在起始时在首端观察到的值来决定。(https://www.xing528.com)

可以用类似的方法来讨论反行特征方程式(4-7)的物理意义:若观察者沿x反方向以速度v运动,其他在线路上任一点x在t时刻所观察到的u(x,t)-Zi(x,t)的值不变,等于两倍反行电压波的数值。图4-20(b)表示反行特征线,是斜率为Z的直线。

根据以上特征方程及其物理概念可以推导出单相无损线的波过程计算的等值电路及其相应的计算公式。

假定有图4-21(a)所示的单相均匀无损线,长度为l,波阻抗为Z,始端(x=0)和末端(x=l)的电压和电流分别为u k(t)、u m(t)、i km(t)、i mk(t)。端点上电流的正方向假设都是从端点流向线路。

根据以上所述特征方程的物理概念,若观察者在t-τ时刻从节点k出发(传播时间τ=l/v),则在时刻t到达m点。从前行特征方程式(4-7)可以得到以下方程

即

若设

则可以有

根据式(4-11)可以得到如图4-21(b)右端所示的线路末端m在时刻t的等值计算电路,而式(4-9)和式(4-11)就是相应的等值计算公式,其中Z是阻值等于线路波阻抗的电阻,I m(t-τ)是等值电流源,它可以根据过去观察的记录,即线路始端在tτ时刻的电压u k(t-τ)和电流i km(t-τ)按式(4-9)计算得到。

同样,观察者可以随反行波从末端节点m运行到始端节点k,根据反行特征方程式(4-7)计算得到

即

若设

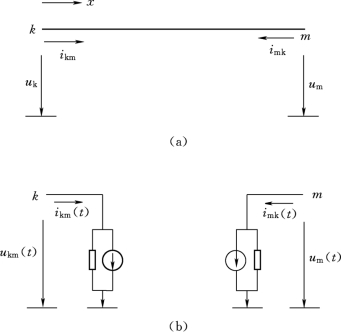
图4-21　单根无损线的等值计算电路

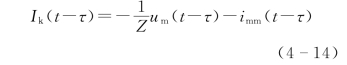
则

根据以上等值计算公式可以得到如图4-21(b)左端所示的线路始端k的等值计算电路。

把等值计算式(4-13)和式(4-15)相结合,就可以得到单根均匀无损线完整的暂态等值计算电路。这一等值计算电路图有两个明显的特点:①在整个分布参数线路的等值计算电路中只包括集中参数电阻(其阻值等于线路波阻抗Z)和等值电流源(其值由线路两端点上的电压和电流在过去的历史记录中计算得到),属于集中参数电路;②在等值计算电路中线路两侧节点k和m是独立分开的,拓扑上没有直接联系(两端点之间互相的电磁联系是通过反映历史记录的等值电流源来实现的),以后可以看到这给电路的求解所带来的方便。

上述单根均匀无损线路等值计算电路由电阻和电流源并联而成,在电路分析中称为诺顿电路。这种电路也可称为暂态伴随电路,因为电路反映线路上的电磁暂态在时间离散点的情况,所以又可称为暂态计算的离散电路。计算波过程的特征线方法通常称作Bergeron方法,因此以上等值电路常称为Bergeron等值计算电路。